Sweet AND

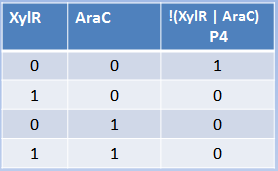
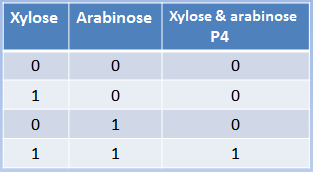
Xylose and arabinose are sugars used by bacteria as carbon sources. XylR and AraC are transcriptional regulators modulated by xylose and arabinose. In this case, the hybrid promoter has as backbone made of the pBAD promoter plus a binding site for XylR. XylR represses the transcription until xylose is present in the cell, the same way that ArsR and CzrA work. AraC represses through the formation of DNA looping. When arabinose enters the cell, it dissolves the loop and transcription starts. We can conclude that arabinose and xylose are essential for the expression of genes under the pBAD/xylR promoter, thus acting as an AND Boolean operation.

Repressors

Inputs

The behavior of both ANDs predicted by our model is consistent with what we expected. From the perspective of the repressors, a higher level of PoPs (Polymerase Per Second, which is a measurement of the level of transcription) is reached when both repressor concentrations are 0, and PoPs start to fall when the concentration of repressors increases, reaching the highest level of repression (lower PoPs) at high concentration of both repressors. This behavior reminds us of the way a NOR behaves, because at low levels of repressor PoPs is high, but for repression, high concentration of one repressor is enough. However, we can't control (directly) the concentration of repressors, so the right way to look at the system is from the perspective of the Input: the metals or the sugars.

If we looked PoPs as a function of the Input, it behaves as an AND logic gate, as can be seen in the continuous TRUTH TABLE. At lower concentrations of Input, the PoPs level is in a very repressed stage. If you keep adding concentration of one of the Input on only one of the axes (yes, axes is the plural of axis), there won’t be high activation until the addition of high concentrations on the other axis. PoPs will increase as the Input concentration increases in a direct proportion fashion.

KAPPA

Sometimes people wonder why we used Kappa, a stochastic approach, to model our system, which was also described by deterministic differential equations. First of all, Kappa helped us come up with the concentration ranges entered in the differential equations (here, an exclamation of awe is usually heard). How did this come to happen? Well, the simulation in kappa is driven by the binding events and is dependent on the species concentrations, so using general kinetic rates we were able to see the dynamic behavior given by the architecture of the network. This allowed us to approximate the final species concentration and look for parameters missing in our ODE system, which was something useful, since we were as lost as a three-legged dog in a rodeo dance.

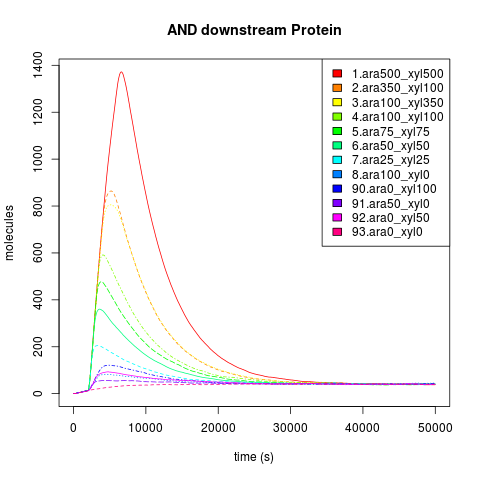
So, first we ran the and_sugar.ka kappa script shifting the sugar initial concentrations in the single input burst and getting the average of 100 iterations to eliminate the noise in the simulation. After running some simulation time, we were happy to see that our "Sweet AND" behaved as expected, that is as an AND. Besides, we were able to see the maximal concentration of the protein that would be downstream of our AND, and the time it took to reach it. As you can see, our simulation grid is not described in its entirety. This is because of the high kappa simulation time consumption, so we chose to feed our ODE system with some parameters and scan the system in a broader manner instead of dying of old age waiting for Kappa. Nevertheless, some behaviors can only be noticed by looking at the simulation grid. For example, the activation of P4 depending on the xylose and arabinose concentrations. As it becomes apparent through a meticulous and insightful analysis only doable by a really smart, handsome, and admirable person, the activation of P4 depends on the concentrations of both, xylose and arabinose. When only one of the two sugars has a high concentration, the activation is not as elevated as when the two have high concentrations.

Xylose	500,000
	350,000
	100,000
	75,000
	50,000
	25,000
	0.0
		0.0	25,000	50,000	75,000	100,000	350,000	500,000
		Arabinose

We can focus only in the dynamics of the downstream protein instead of the dynamic of all the system. This plot describes the time to reach steady state and maximal concentration of the AND downstream protein. It also describes what the maximal concentration of the AND protein is. All of this is based on a single input burst concentration.

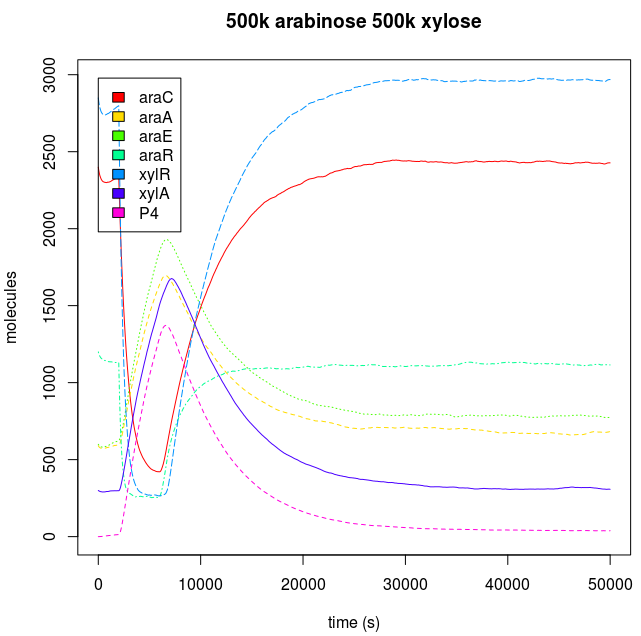
Endogenous system and Downstream protein dynamic is dependent of the kind of input.

The inputs used by each AND have a unique effect in the response of the cell, because carbohydrates are degraded by the cell. When we add sugars to the sweet AND system, if they are added just like a discrete and unique dose of them, the cell will react to the alteration through the activation of the degradation machinery, and when the sugar pool gets empty, the cell achieves a similar state to the one before the sugar was introduced. When the sugar addition is constant, the cell has a complete phenotypic change, reaching a new steady state.

Transfer Function

Our logic AND gates are fully dependent on the intracellular concentrations of the inducer (in this case, xylose and arabinose). Then, to accomplish our duty in model, we use the "Transfer Function", for which it is necessary to take into account the regulation and dynamics of the endogenous B. subtilis intake-efflux system that controls the intracellular concentrations of sugars. All of this is going to be the "Black Box".

So, our first task was to reconstruct the regulatory network of B. subtilis for the intake-efflux system. The regulation data was retrieved from several papers and databases like [http://bsubcyc.org/ http://bsubcyc.org/]