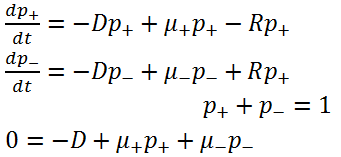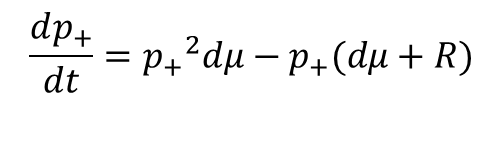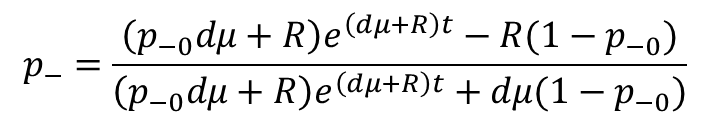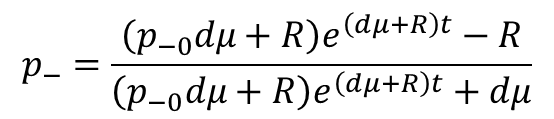Team:NTU-Taida/Modeling/Plasmid-Stability
From 2012.igem.org
| Line 45: | Line 45: | ||
<!--EOF--> | <!--EOF--> | ||
| - | {{:Team:NTU-Taida/Templates/ContentEnd}}{{:Team:NTU-Taida/Templates/Footer|ActiveNavbar=Modeling, #nav- | + | {{:Team:NTU-Taida/Templates/ContentEnd}}{{:Team:NTU-Taida/Templates/Footer|ActiveNavbar=Modeling, #nav-Modeling-Plasmid}} |
Revision as of 20:20, 26 September 2012
Plasmid-Instability-Model
Modeling and Application
How to model plasmid instability:
We use Cooper's model (Cooper, N.S., M.E. Brown, and C.A. Caulcott, A ) to model plasmid instability, and set a protocol to suggest users which modules can be used to prove their system stability.
Cooper’s model: Under steady state, population distribution of bacteria follows underlying equation:
Growth rate and dilution rate have such relation:
Substitute in
produce
This equation belongs to the Bernoulli form of Differential equation and can be solved as:
Initially, plasmid loss usually is 0. ![]() So the equation can be simplified as:
So the equation can be simplified as:
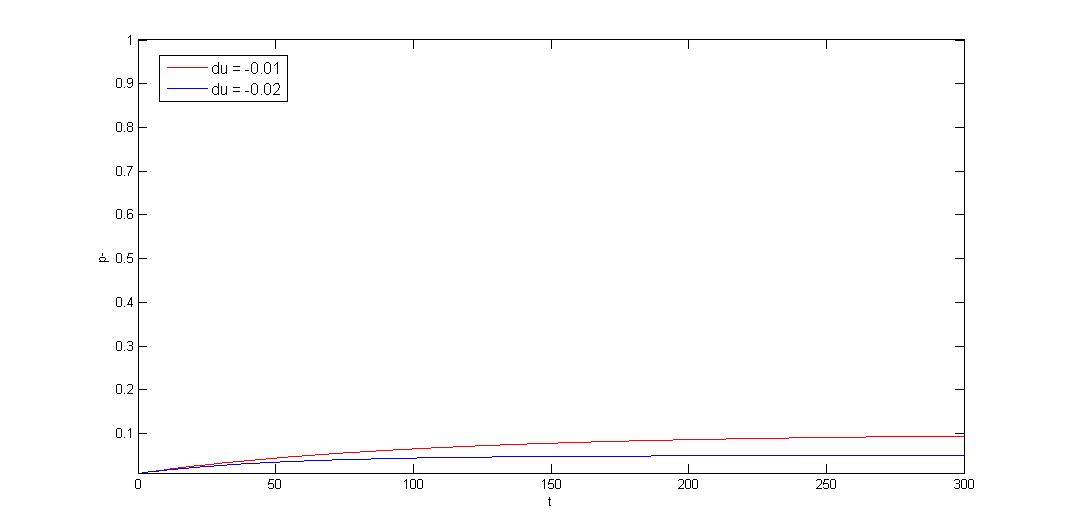
There can be three kinds of plasmid instability condition:
1.Growth rate difference >> segregation instability
2.Growth rate difference =< segregation instability
3.Negative growth rate difference >> segregation instability
Knowing the condition of your expression system is important, if growth rate difference is much greater than segregation instability, partition system cannot help stabilize such system. We will show how to discriminate between three conditions and how to use our parts to solve the condition.
1.Growth rate difference >> segregation instability![]()
The equation can be further simplified.
2.Growth rate difference =< segregation instability![]()
3.Negative growth rate difference >> segregation instability![]()
 "
"