plasmid instability modeling:

We use Cooper's model (Cooper, N.S., M.E. Brown, and C.A. Caulcott, A ) to model plasmid instability, and set a protocol to suggest users which modules can be used to prove their system stability.

Cooper’s model: Under steady state, population distribution of bacteria follows underlying equation:

$$\frac{dp_+}{dt}=-Dp_++\mu_+p_+-Rp_+$$ $$\frac{dp_-}{dt}=-Dp_-+\mu_-p_-+Rp_+$$ $$p_++p_-=1$$ $$0=-D+\mu_+p_++\mu_-p_-$$

p_-

Plasmid-free ratio

p₊

Plasmid retained ratio

D

Dilution rate

R

Plasmid loss rate(R=Muation rate+Segregational instability)

\(\mu\)

Growth rate

Growth rate and dilution rate have such relation:

$$\mu_-=D+p_+d\mu$$ $$\mu_+=D-p_-d\mu$$ $$(d\mu=\mu_--\mu_+)$$

Substitute in

$$\frac{dp_+}{dt}=-Dp_++\mu_+p_+-Rp_+$$

produce

$$\frac{dp_+}{dt}=p^2_+d\mu-p_+(d\mu+R)$$

This equation belongs to the Bernoulli form of Differential equation and can be solved as:

$$p_-=\frac{(p_{-0}d\mu+R)e^{(d\mu+R)t}-R(1-p_{-0})}{(p_{-0}d\mu+R)e^{(d\mu+R)t}+d\mu(1-p_{-0})}$$

Initially, plasmid loss usually is 0.\(p_{-0}\gg1\) So the equation can be simplified as:

$$p_-=\frac{(p_{-0}d\mu+R)e^{(d\mu+R)t}-R}{(p_{-0}d\mu+R)e^{(d\mu+R)t}+d\mu}$$

Three kinds of plasmid instability condition:

1.Growth rate difference \(\gg\) segregation instability
2.Growth rate difference \(\leq\) segregation instability
3.Negative growth rate difference \(\gg\) segregation instability

Knowing the condition of your expression system is important, if growth rate difference is much greater than segregation instability, partition system cannot help stabilize such system. We will show how to discriminate between three conditions and how to use our parts to solve the condition.

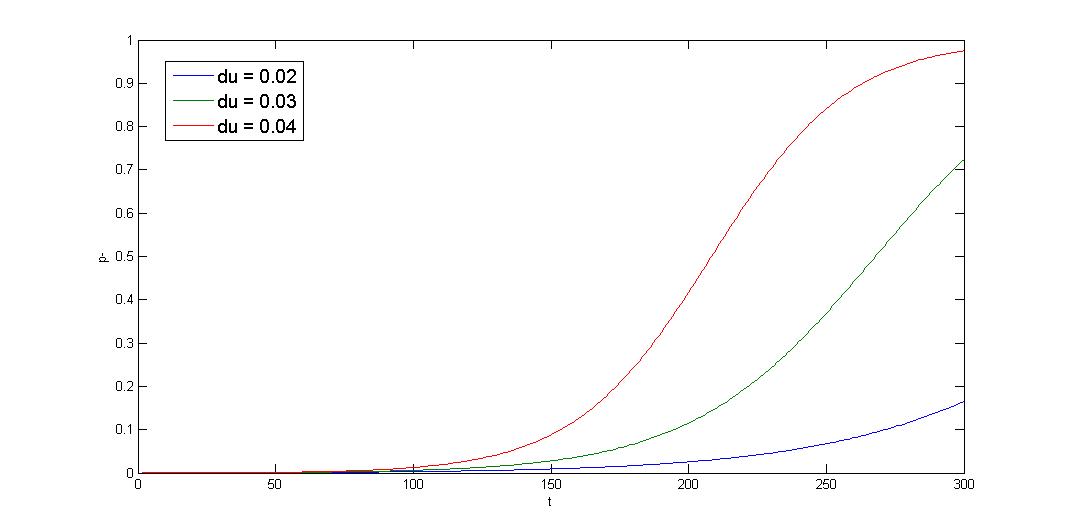
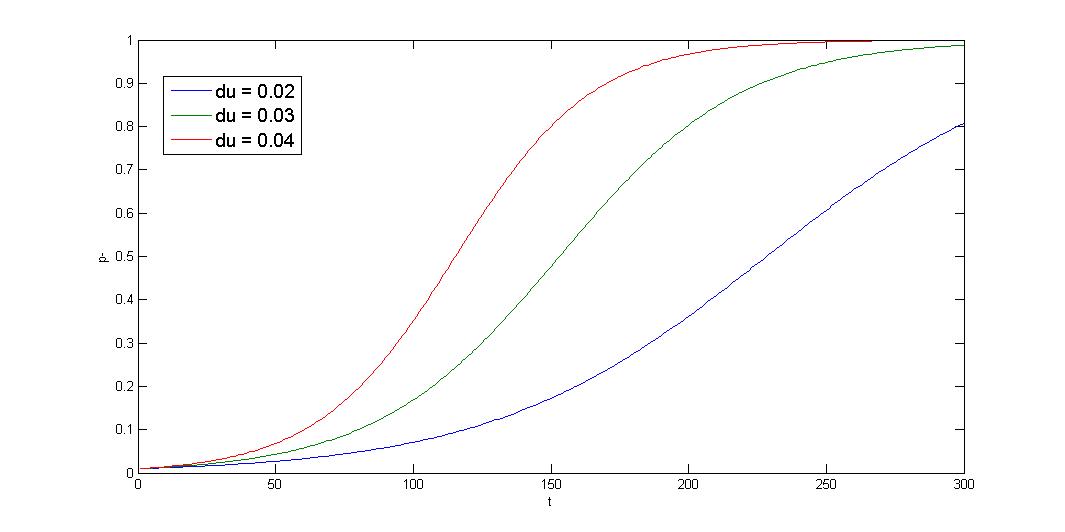
1.Growth rate difference \(\gg\) segregation instability, \(d\mu\gg R\)

The equation can be further simplified.

$$p_-=\frac{(p_{-0}d\mu+R)e^{(d\mu+R)t}-R(1-p_{-0})}{(p_{-0}d\mu+R)e^{(d\mu+R)t}+d\mu(1-p_{-0})}$$ $$\rightarrow p_-\approx(p_{-0}+\frac{R}{d\mu})e^{d\mu t}-\frac{R}{d\mu}$$

R=10^-5 x-axis:generation y-axis:p- ratio

R=10^-5 init=0.01 x-axis:generation y-axis:p- ratio

The simulation shows that initial condition greatly affect the result, and the curve is sigmoid. The segregation instability shows minor effect on the plasmid loss rate (not shown). So that plasmid loss derive mainly from growth rate difference, reduce burden effect is primary mission. Avoid protein/RNA overexpression, and reduce gene dosage; most important of all, well-designed circuit. Our multimer resolution system might reduce dimer caused metabolic burden.

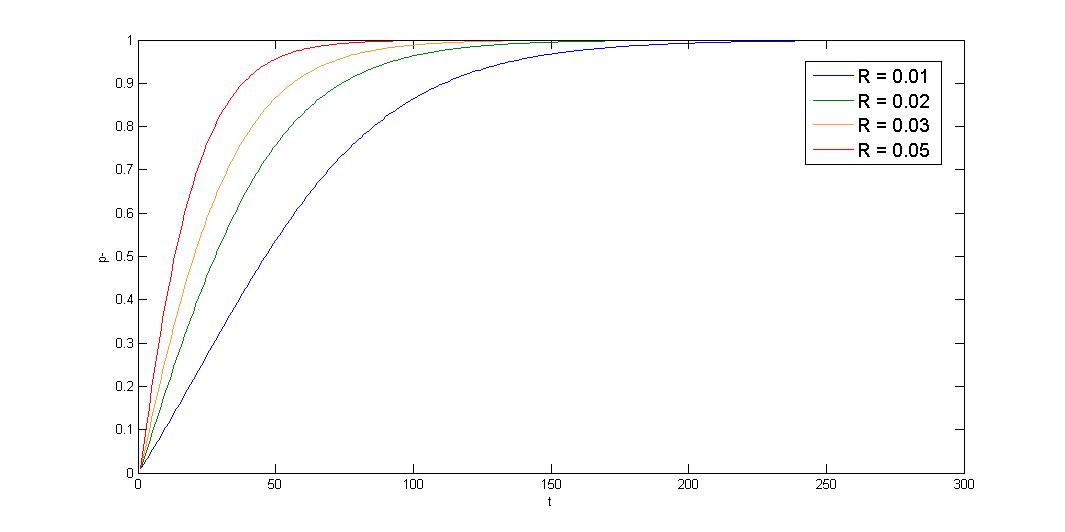
2.Growth rate difference \(\leq\) segregation instability, \(d\mu\leq R\)

$$p_-\approx1-(1+\frac{d\mu}{R})e^{-(d\mu+R)t}+\frac{d\mu}{R}(1+\frac{d\mu}{R})e^{-2(d\mu+R)t}$$

Under this condition, plasmid-bearing cell shows exponential decay. Segregation instability greatly affect the stability. Our partition system and our toxin-antitoxin can solve the problem, multimer resolution system can also relieve the multimer caused segregation instability.

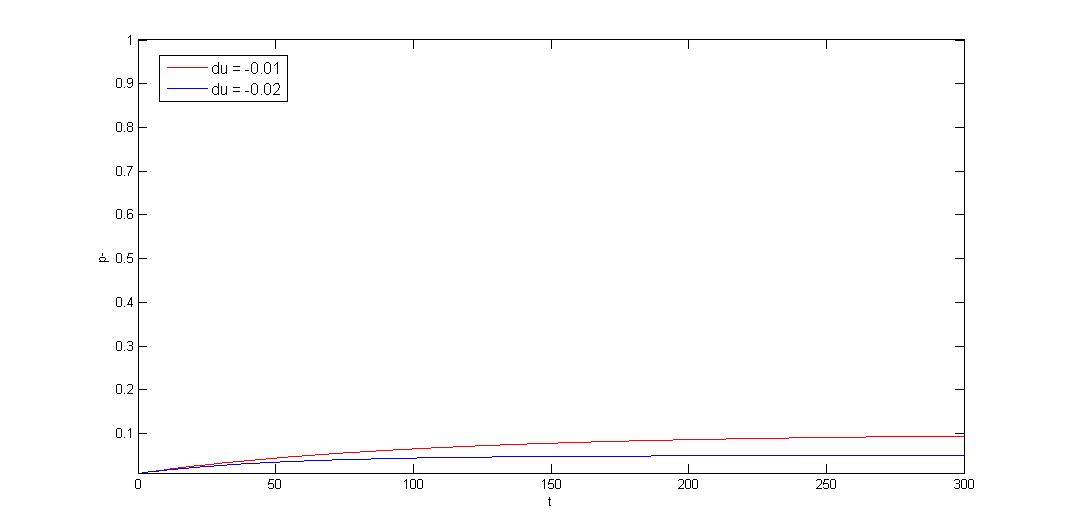
3.Negative growth rate difference \(\gg\) segregation instability, \(d\mu\leq0,|d\mu|\gg R\)

$$p_-=\frac{(p_{-0}d\mu+R)e^{(d\mu+R)t}-R(1-p_{-0})}{(p_{-0}d\mu+R)e^{(d\mu+R)t}+d\mu(1-p_{-0})}$$ $$t\rightarrow \infty, p_-\rightarrow p^*=\frac{R}{|d\mu|}$$

If plasmid provide host selective advantage(ex:antibiotic resistant gene under antibiotic selection pressure), plasmid loss/plasmid retained ratio will approach a constant: P*. Segregation instability will decide the constant.

Our partition system and our toxin-antitoxin can reduce the constant.

Reference

1. Cooper, N.S., M.E. Brown, and C.A. Caulcott, A Mathematical Method for Analyzing Plasmid Stability in Microorganisms. Journal of General Microbiology, 1987. 133: p. 1871-1880.