Team:OUC-China/Modeling/ODEModel
From 2012.igem.org
ODE Model
ODE simulation
Aim: To verify feasibility of ratio sensor & comparator theoretically
Steps:
1. Establish ODE equations based on Mass-action law;
2. Investigate reasonable parameter sets from previous researches;
3. Simulation;
4. Verify the feasibility of devices.
Results:Both Ratio Sensor and Comparator are feasible within the affordable range in vivo. However, the parameter space of Ratio sensor is not wide enough, which adds uncertainty on constructing such a device.
Background
Simulation based on mass-action law is a common method of modeling sRNA regulation[1].
Generally, we perform our simulation under the guidance given below

The differences on design between ratio sensor and comparator is noted in the project page.
Considering the RNA pairing reaction as chemical reaction,we will see the probability of collision is determined by their concentration, and the probability of pairing after collision is determined by their affinity(that is reaction constant k in mass-action law).

Noting that the input(extra inducer concentration) controls alphas & alpham(RNA synthesis rate), we formulated the mechanism above quantitatively via a simple kinetic model(ODE model) for three RNA interaction. The model is cast in terms of two mass-action equations for the cellular concentrations of the sRNA ([s1],[s2]) and its target GFP mRNA ([m]):



Is it feasible?In this ternary system,there are at least 6 parameters uncertain,we verified the feasibility of constructing such a device through ODE simulation using parameter set from previous researches, fortunately,it is viable theoretically within the affordable parameter range in cell, and the apparent enough with the presence of noise
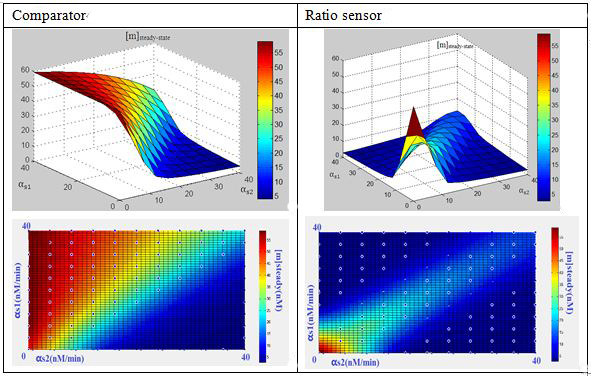
ComparatorFor comparator, simple conclusions could be drawn:
When as1/as2>1, [m]steady state=0;
When as1/as2<1, [m]steady-state=60
Considering the mechanism of comparator as a molecular titration,we also expect a ultra-sensitivity behavior at the switch point(as1/as2=1),which will contribute to the “comparing” decision-making behavior.
Ratio sensorFor ratio sensor, an apparent peak can be observed when as1/as2=1
We run a supplementary simulation at point of as1:as2=1, making comparisons when as1:as2=1:1 and as1:as2=1:2(Fig.3)



Fig 3.
Discussion: The three differential equations are established based on Erel Levine et al and we have made a further development. In addition, our model has changed from the one for single interaction between sRNA and mRNA to the one for three kinds of interaction (s1RNA and s2RNA, s1RNA and mRNA, s2RNA and mRNA ). Therefore the latter model would come as a meaningful example for researchers to explore more interactions among RNAs. Of course, we can get the model, to a large degree, due to the creative achievement of Erel Levine et al and others.
References
[1] Levine, E., et al., Quantitative characteristics of gene regulation by small RNA. PLoS biology, 2007. 5(9)
[2] Nicolas E. Buchler1, Matthieu Louis, Molecular Titration and Ultrasensitivity in
Regulatory Networks, J. Mol. Biol. (2008) 384, 1106–1119
 "
"
 Home
Home
 HumanPractice index
HumanPractice index
 JudgingForm
JudgingForm
 Contact Us
Contact Us
 Project Overview
Project Overview
 Sensor
Sensor
 Decision-making Device
Decision-making Device
 Gas vesicle
Gas vesicle
 ODEModel
ODEModel
 Parameter Sensitivity Analysis
Parameter Sensitivity Analysis
 Parameter Sweep
Parameter Sweep
 Noise Analysis
Noise Analysis
 HumanPractice Overview
HumanPractice Overview
 Meeting and Academic Communication
Meeting and Academic Communication
 Camps, Class and Lectures
Camps, Class and Lectures
 Special HP
Special HP
 Team Members
Team Members
 Instructors
Instructors
 Acknowledgement&Cooperation
Acknowledgement&Cooperation
 Lab
Lab
 Parts
Parts
 Safety
Safety
 Labnote
Labnote
 Modeling Note
Modeling Note
 Protocols
Protocols

