Team:TU-Delft/Modeling/Diffusion
From 2012.igem.org


One of the main objectives of the project was to synthesize a practical device, the Snifferometer for tuberculosis detection. As a first step towards achieving this goal, we built a temporal model of the system using PDE's which was simulated in matlab. A 2D reaction-diffusion system was then implemented in COMSOL multiphysics using the knowledge obtained from single cell pathway model,ombining the behaviours of the which helped us get a better understanding of how such a device could be implemented and the response times involved in such a process.
Contents |
Diffusion Model
Setup of diffusion model
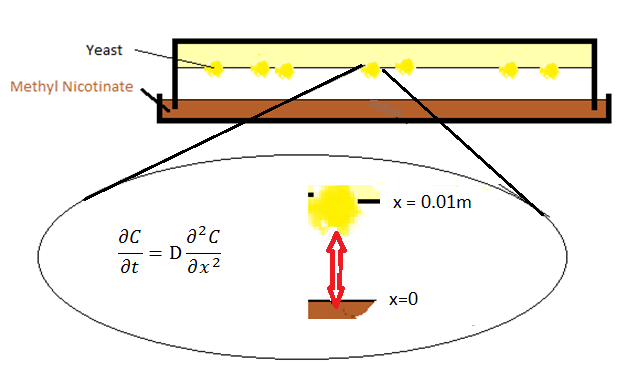
The diffusion setup contains two parts: a petridish of odor liquid/solid in the bottom and agar of olfactory yeast on the top. The odor molecular diffuses through gas from petridish to agar.
Approach
PDEs
The diffusion model is built by PDEs.

where C represents the ratio of pressures between gasphase and atmosphere, x is the distance from the surface of petridish, and D is the diffusion coefficient, of which value is cited from [1].
In order to solve PDEs, numerical methods are used as approximation.
On the left side of the equation, the Euler forward method is taken:

On the right side of the equation, the central differential method is used:

Left side equals to right side

Therefore, the PDEs can be numerically replaced by the equation:

where 
Boundary conditions
In order to solve this equation, boundary conditions are required. Two boundary conditions are set for these two surfaces of petridish-gas and gas-agar.
- At x=0, the Dirichlet boundary condition was placed:

with Csat being the pressure ratio with respect to the saturation pressure of the specific compound being IsoAmylAcetate as an example in our model. For IsoAmylAcetate this value is 533.3 Pa at room temperature. Thus Csat is equal to 0.05333.
- One can take Neumann boundary condition at x=l, where l is the distant between petridish and agar and assumed to be 0.01 meter in the model. The reason we can use Neumann boundary is because the molecules bounce back into the gasphase against the agar surface.

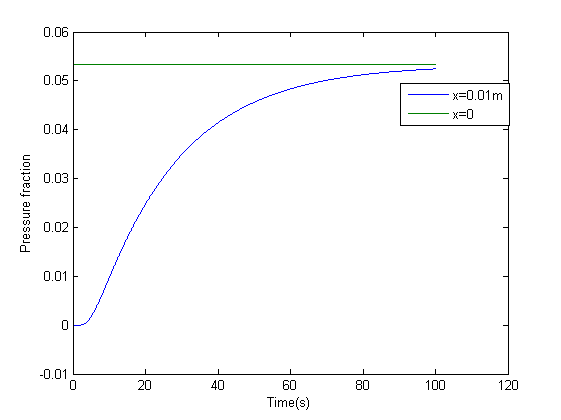
Simulation result
Figure 2 shows the simulation result with distance dimension 0 - 0.01 meter and the time dimension 0 - 100 seconds. From Figure 3 it can be seen after 100 seconds it approximately reaches steady state at the x=0.01 boundary.
Snifferometer
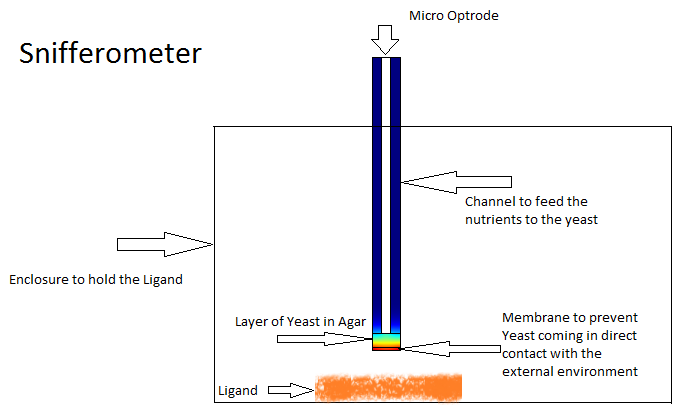
One of the other goals of the diffusion modeling was to model the device which we intended to build for the project. We made use of the finite element analysis simulator Comsol Multiphysics[3]
for developing this model.Different models were analyzed for their suitability before coming to the final design in Figure. The device at the bottom has a membrance preventing the yeast coming in direct contact with external substances, above which is a layer of agar in which yeast is placed, the nutrients for it's growth is fed in through a channel along the sides of the tube using which the yeast cells can also be replaced as and when needed. A micro-optrode is then used to sense the photons emitted by the fluoroscent proteins.
Saliva Model
References
1. Chen, N. H. (1962). New Generalized Equation for Gas Diffusion Coefficient. J. Chem. Eng. Data, 37–41.
 "
"