Team:TU-Delft/Modeling
From 2012.igem.org
(→Future Work) |
(→Research Cycle) |
||
| Line 43: | Line 43: | ||
At the beginning, based on biological expertise and literature surveys, hypotheses of model structures are proposed. However, due to the inadequate descriptions of dynamics and lack of information, analyses of hypothesized models are necessary to investigate the properties of models, including the analyses of parameter sensitivities and structural stability in pathway model. Then, experiments can be comprehended and even designed by the knowledge of model simulation. For example, based on the understanding of diffusion model, a practical device is designed, and the output of our device can be predicted. | At the beginning, based on biological expertise and literature surveys, hypotheses of model structures are proposed. However, due to the inadequate descriptions of dynamics and lack of information, analyses of hypothesized models are necessary to investigate the properties of models, including the analyses of parameter sensitivities and structural stability in pathway model. Then, experiments can be comprehended and even designed by the knowledge of model simulation. For example, based on the understanding of diffusion model, a practical device is designed, and the output of our device can be predicted. | ||
| - | The measured data from "wet" experiment, in turn, modifies the model by tuning the parameters and eliminating inconsistent assumptions. One example is in pathway model ambiguous assumptions of stability is resolved by measured output GFP. | + | The measured data from "wet" experiment, in turn, modifies the model to fit the reality by tuning the parameters and eliminating inconsistent assumptions. One example is in pathway model ambiguous assumptions of stability is resolved by measured output GFP. |
Finally, the valid model give a good explanation for the biological practice and give "cheap" predictions for different conditions instead of the time-consuming experiment. | Finally, the valid model give a good explanation for the biological practice and give "cheap" predictions for different conditions instead of the time-consuming experiment. | ||
Revision as of 14:04, 26 September 2012


Contents |
Overview
We decided to use the modeling expertise of the team members to achieve three key objectives for our project.
- Develop scientific understanding of the yeast pheromone response pathway.
- Test the effects of the changes to the system.
- Aid decision making in the laboratory.
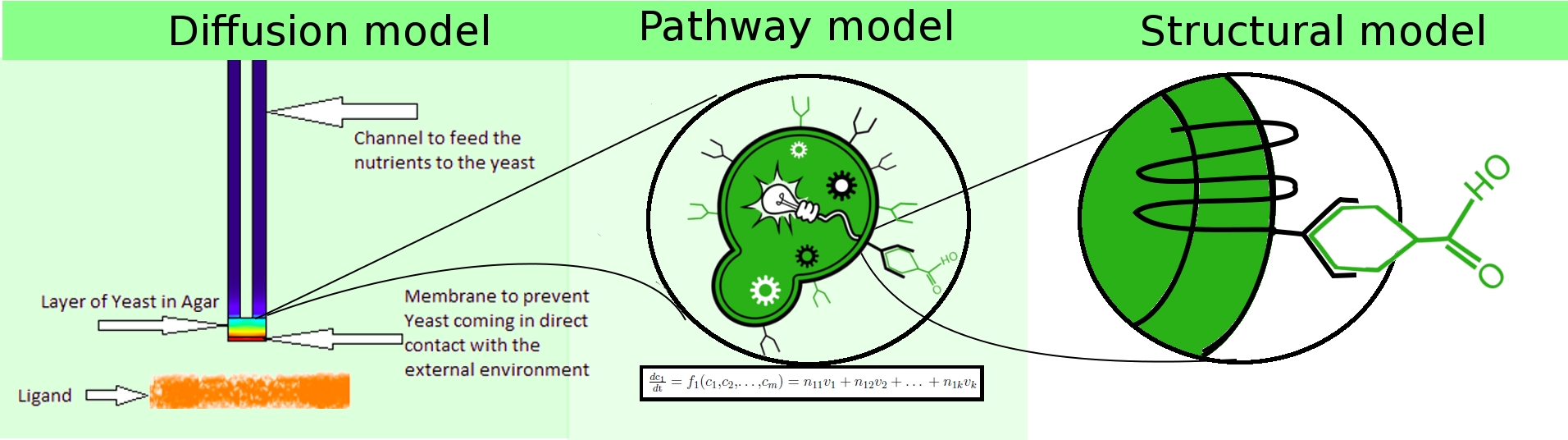
To achieve the stated objectives, three different models were built for a multi-level modeling approach, with heterogeneous models spanning
- population dynamics (diffusion model).
- extra-cellular interactions (structural model).
- intra-cellular dynamics (pathway model).
Connected Multi-level Models
These three models interact with each other to represent the mechanism of our project in different perspectives. At the system level, diffusion model sheds light on how the oder in the petridish diffuses through gas into the disk of olfactory yeasts, which imitates the diffusion process in real life such as smelling banana by human. As a downstream of receiving odor ligands, the pathway model is built to functionally simulate the intra-cellular biochemical reactions in the signalling pathway. Parameters in pathway were fitted to the experimental data thus it can give a good estimation on how the important intra-cellular species evolve and predict the producing fluorescence in the experiment. Moreover, the structural model is designed to understand the ligand docking at the molecular level. It indicates how well the hydrogen bonds are and how stable of activated receptor, which give an insight into rates of receptor inactivation in the pathway model. Further research of structural model on receptor binding and niche shrink in volume may provide more knowledge about binging rate and G protein release.
Based on these models, a practical device, Snifferometer is designed to achieve the purpose of odor detection. The model of this device is developed to give an idea of the application of our project.
The models span a broad spectrum of techniques: PDE, MD (molecular dynamics), SDE and ODE, as well as alignment techniques. Various and diverse tools have been employed: COMSOL, YASARA, MATLAB, COPASI, BLAST.
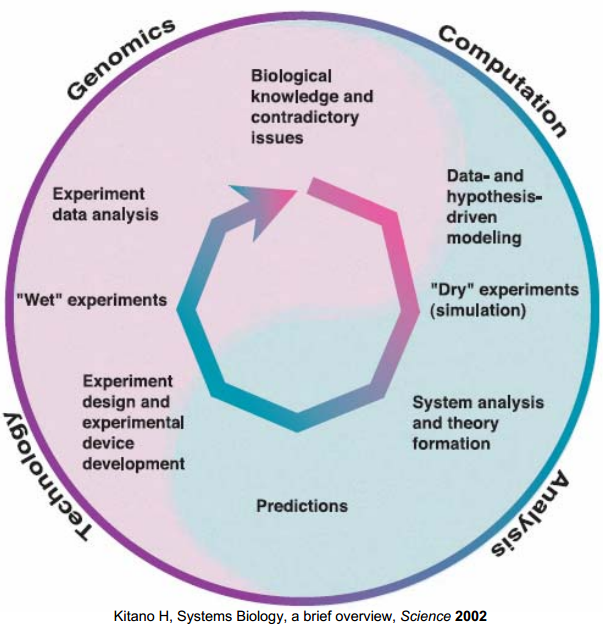
Research Cycle
A cycle of research is an interactive boundary work between wetlab and "dry" modeling to gain a systematic understanding of our biological network.
At the beginning, based on biological expertise and literature surveys, hypotheses of model structures are proposed. However, due to the inadequate descriptions of dynamics and lack of information, analyses of hypothesized models are necessary to investigate the properties of models, including the analyses of parameter sensitivities and structural stability in pathway model. Then, experiments can be comprehended and even designed by the knowledge of model simulation. For example, based on the understanding of diffusion model, a practical device is designed, and the output of our device can be predicted.
The measured data from "wet" experiment, in turn, modifies the model to fit the reality by tuning the parameters and eliminating inconsistent assumptions. One example is in pathway model ambiguous assumptions of stability is resolved by measured output GFP.
Finally, the valid model give a good explanation for the biological practice and give "cheap" predictions for different conditions instead of the time-consuming experiment.
Future Work
1. fit and validate structural model
2. stochastic model for the whole pathway.
3. diffusion model of blowing gas
4. estimation of minimum amount of ligand by structural model and pathway model
Diffusion Model
Structural Model
Pathway Model
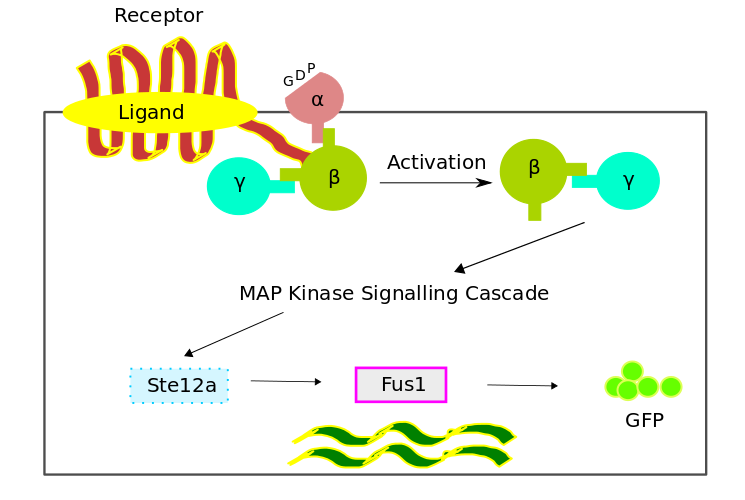
The bio-chemical pathway model was developed based on a scheme favouring the temporal order of the processes, which involved the four fundamental modules,
- Receptor Activation
- G - Protein Cycle
- MAPK Cascade
- Gene Expression
Three different models were used for the analysis of different aspects of the pathway. The dynamics of the system in these models were described using a set of differential equations governing the concentration changes of individual components and of complexes over time. On account of the gene expression module being noisy, a stochastic model of the gene expression module was implemented using stochastic differential equations.
Sensitivity and stability analysis were permformed to determine the sensitivity coefficients which were used to study the parametric dependence of the biological models. The results from the sensitivity analysis were then used in the parameter estimation to fit the model to the data provided by the experimentalists.
References
1.Kitano, H. Systems biology: a brief overview. Science 295, 1662–1664 (2002)

 "
"