Team:TU-Delft/Analysis
From 2012.igem.org
| Line 15: | Line 15: | ||
If the rate of receptor degradation is larger than the rate of receptor generation, the receptor will dissipate towards zero in the end. | If the rate of receptor degradation is larger than the rate of receptor generation, the receptor will dissipate towards zero in the end. | ||
| - | [[File:|800px|left|thumb|'''Figure | + | [[File:receptorDegradation.png|800px|left|thumb|'''Figure 2''': Structure of dissipating receptor.]] |
In analysis, there is only one steady state and no bifurcation. Moreover, the system is stable around the steady state. | In analysis, there is only one steady state and no bifurcation. Moreover, the system is stable around the steady state. | ||
Revision as of 13:23, 21 September 2012
System analysis
Contents |
Stability analysis
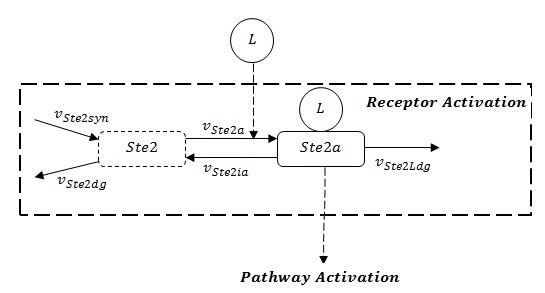
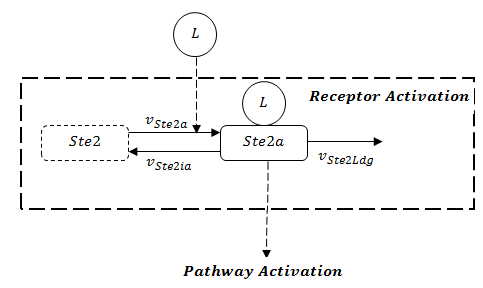
In figure 3.1, we can see the receptor activation is the prerequisite to activate the whole pathway. The stability of the whole pathway is decided by the state of receptor, as it shows in Figure 1. However, before parameter estimation by using experimental data, because both values of rates to synthesize and to degrade the receptor are unknown, there are two possibilities for the evolution of receptor: dissipation or constant.
In the case of dissapating Ste2
If the rate of receptor degradation is larger than the rate of receptor generation, the receptor will dissipate towards zero in the end.
In analysis, there is only one steady state and no bifurcation. Moreover, the system is stable around the steady state.
Because of mass balance and dying out Ste2a (Ste2), the following pathway will recover to the initial concentration which leads to GFP degrade to zero asymptotically.
When analysing the system by linearization as above, the eigenvalues of full Jacobian A contains both zeros and values of negative real-part, leading to undertermined conclusion for original nonlinear system. However, because of mass balance, 6 out of total 17 species are conserved values including Sst2a (Sst2), Fus3a (Fus3), Ste12 (Ste12a), and GaGTP, C, D in the big cycle of combining G-protein and MAPK cascade. They are linear combinations of particle numbers that do not vary during the time evolution of the system. Each conservation relation can be used to eliminate one variable of the system, leading to a reduced system with a smaller number of variables. These variables are called the independent variables of the system; the dependent variables are defined as linear combinations of independent variables.Technically finding the conservation relation means finding rows in the stoichiometry matrix that can be expressed as linear combinations of other rows.
By using COPASI which uses Householder QR factorization [9] to reduce model, the Jacobian of reduced model can be calculated and its eigenvalues are
In the case of accumulating or constant Ste2
If the rate of receptor degradation is larger than the rate of receptor generation, the receptor will accumulate till reaching the possible maximum value. The pathway will continuously be activated, and GFP accumulates without constraints, so the system is unstable.
Sensitivity analysis
Values can be tuned: initial concentration of Ste2, Vht2hd, VGa2ht, VGFPmRNAsyn
 "
"