Team:TU-Delft/Analysis
From 2012.igem.org
| Line 8: | Line 8: | ||
</body> | </body> | ||
| - | <img src="https://static.igem.org/mediawiki/igem.org/ | + | <img src="https://static.igem.org/mediawiki/igem.org/6/67/Pathwaymodel.jpg" align="middle" width="100%"></html> |
<div id="contentbox" style="text-align:justify;"> | <div id="contentbox" style="text-align:justify;"> | ||
Stability and time-dependant sensitivity analyses were implemented for the deterministic pathway model. | Stability and time-dependant sensitivity analyses were implemented for the deterministic pathway model. | ||
Latest revision as of 01:42, 27 October 2012


Stability and time-dependant sensitivity analyses were implemented for the deterministic pathway model.
Contents |
Stability analysis
A steady-state analysis can be done using even only the network structure, without knowing the rate constants for particular reactions. In the pathway model, we can see the receptor activation is the prerequisite to activate the whole pathway. The stability of the whole pathway is decided by the state of receptor. The full structure of receptor is showed in Figure 1.
However, before parameter estimation by using experimental data, there are two possibilities for the evolution of receptor: dissipation or constant, because both values of rates to synthesize and to degrade the receptor are unknown. In correspondence, two results, either stable or unstable, might be possible because of lack of information. The stability analysis for both cases is implemented in the later parts.
Then, from the collected experimental data (see in Pathway Model, parameter estimation), we found the output GFP decreases after reaching the peak sometime, which matches the case of dissipating Ste2.
Conclusion
The system is stable by analysing the single cell pathway model.
In the case of dissipating Ste2
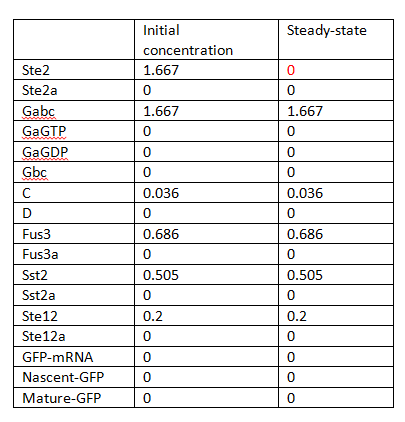
If the rate of receptor degradation is larger than the rate of receptor generation, the structure of receptor can be functionally simplified as Figure 2. The receptor will dissipate towards zero in the end. As a consequence, the states in the following pathway will recover to the initial states based on mass balance. Thus, GFP will definitely degrade to zero asymptotically.
In this sense, there is only one steady state and no bifurcation, and the system seems to be stable. The steady states are listed in Table 1.
In order to test the stability around the steady states, the linearization method is used for this nonlinear system.

By computation, the eigenvalues of full Jacobian A contain both zeros and the values with negative real-part, leading to undertermined conclusion for the stability of original nonlinear system. However, because of mass balance, there are some conserved values which can be reduced. They are linear combinations of particle numbers that do not vary during the time evolution of the system. Each conservation relation can be used to eliminate one variable of the system, leading to a reduced system with a smaller number of variables. These variables are called the independent variables of the system; the dependent variables are defined as linear combinations of independent variables.Technically finding the conservation relation means finding rows in the stoichiometry matrix that can be expressed as linear combinations of other rows [1].
By using COPASI which uses Householder QR factorization [2] to reduce model, the Jacobian of reduced model can be calculated and its eigenvalues are showed in Table 2. 6 out of total 17 species are conserved values including Sst2a (Sst2), Fus3a (Fus3), Ste12 (Ste12a), and GaGTP, C, D in the big cycle of combining G-protein and MAPK cascade.
In the case of accumulating or constant Ste2
If the rate of receptor degradation is smaller than the rate of receptor generation, the receptor will accumulate till reaching the possible maximum value. The pathway will keep activating once activated, and GFP will accumulate without limit, so the system is unstable.
Sensitivity analysis
Motivation of sensitivity analysis
Sensitivity analysis is to study how system variables depend on model parameters normally including two aspects: kinetic rates and initial concentrations. There are a couple of reasons to do sensitivity analysis.
- Validation of model with respect to uncertainty. When there is limited or no data for a conceptual model, one venue for model validation is to test the sensitivity of a given parameter fit. Thus, a model that is touted for its qualitative behaviour without quantitative behaviour can show that these properties are conserved when there is perturbation to the presented model.
- Better choice for the parameter estimation. In the presence of a small data set and many parameters, responses will not change equally to similar changes in parameters: some are sensitive and some are not. The parameter space we wish to fit can be reduced by examining which parameters are sensitive and which are not.
- Parameter tuning for the optimal experiment design. The original parameters in the experiment may be not efficient. In order to achieve better performance, some parameter can be tuned, such as the initial concentration of Ste2, the rate of Gbc synthesis, Gabc synthesis and mRNA synthesis in our project. Sensitivity analysis can provide how the output evolve when certain parameters are changed.
Time-dependant sensitivity analysis
The output GFP is the variable of interest for our experiment, thus the sensitivity analysis is on the GFP rather than all species in the pathway model.
Values of the parameters are cited from related paper, which is stated in detail in the page Single Cell Model.
A standard sensitivity analysis investigate the changes in the steady-state values of variables of interest with respect to the changes in the model parameters. However, time-dependant sensitivity analysis is chosen instead of steady-state analysis. This is becasue there is no multi steady states for GFP and the steady state might be not able to reach during the course of observation. Moreover, sometimes it is more important to know how the values of sensitivity evolve with the time. [3]

V represents the variable we are interested, while p is the perturbed parameters. When initial concentrations are considered as perturbed parameters p, some of them are zero, as shows in Table 1. In order to avoid the meaningless sensitivities, the largest magnitude of each concentration is taken instead.
Sensitivity of rates
By varying the input from 0.002 to 20 micromolar and the magnitude of perturbation from 20% to 300%, all of these sensitivity analysis conclude the same ranking of sensitivity, in which only 3 rates are really important to the output and the sensitivities of other rates are lower than 1%, as shows in Table 3.
Sensitivity of initial concentrations
By varying the input from 0.002 to 20 micromolar and the magnitude of perturbation from 20% to 300%, time-dependant sensitivities of initial concentrations are plotted in Figure 7, 8, and 9. Four of initial concentrations have very high sensitivities on output, while some of them can be even ignored because of super low sensitivities. Table 4 lists the sensitivity ranking in decrement order.
Conclusion
sensitivity rankings of rates and initial concentrations are obtained and listed in Table 3 and Table 4 respectively.
- Matlab script for Sensitivity Analysis can be found here.
 "
"