Team:NTU-Taida/Modeling
From 2012.igem.org
(→Single Cell Model) |
(→Single Cell Model) |
||
| Line 6: | Line 6: | ||
{| align="center" | {| align="center" | ||
| - | + | | $$X_{FadR}=FadR\times (\frac{\beta^{n2}_{FadR}}{FA^{n2}+\beta^{n2}_{FA}})$$ | |
| - | $$\frac{\text{d}TetR_{1}}{\text{d}t}=\alpha_{TetR_{1}}\times (\frac{\beta^{n1}_{FadR}}{\beta^{n1}_{FadR}+X^{n1}_{FadR}})-\gamma_{TetR_{1}}\times TetR_{1}$$ | + | |$$\frac{\text{d}TetR_{1}}{\text{d}t}=\alpha_{TetR_{1}}\times (\frac{\beta^{n1}_{FadR}}|{\beta^{n1}_{FadR}+X^{n1}_{FadR}})-\gamma_{TetR_{1}}\times TetR_{1}$$ |
| - | $$\frac{\text{d}LuxI}{\text{d}t}=\alpha_{LuxI}\times (\frac{\beta^{n1}_{FadR}}{\beta^{n1}_{FadR}+X^{n1}_{FadR}})-\gamma_{LuxI}\times LuxI$$ | + | |$$\frac{\text{d}LuxI}{\text{d}t}=\alpha_{LuxI}\times (\frac{\beta^{n1}_{FadR}}{\beta^{n1}_{FadR}+X^{n1}_{FadR}})-\gamma_{LuxI}\times LuxI$$ |
| - | $$\frac{\text{d}FadR}{\text{d}t}=\alpha_{FadR}-\gamma_{FadR}\times FadR$$ | + | |$$\frac{\text{d}FadR}{\text{d}t}=\alpha_{FadR}-\gamma_{FadR}\times FadR$$ |
| [[File:NTU-Taida-Model-Single-Overview-Time-Response.png|450px|thumb|center]] | | [[File:NTU-Taida-Model-Single-Overview-Time-Response.png|450px|thumb|center]] | ||
Revision as of 08:44, 26 October 2012
Modeling Overview
To evaluate the synthetic network designs in our Pepdex system, we performed thorough analysis of our anti-obesity device by created a series of computational models describing the circuit in our E.coli cells, the communications between cells, and the dynamic change in their extracellular environment.
Contents |
Single Cell Model
To get started, we designed a single cell model based on ordinary differential equations to simulate the function of our entire system in a single E.coli cell. In order to have a better experimental (wet) characterization of each module, we performed functional tests for each module individually – i.e. PfadBA-RBS-mRFP (BBa_K817033) to characterize the biosensor, J23119 (constitutive promoter)-RBS-SP1-GLP1-xx (BBa_K817008) to characterize our peptide effector, etc. With the single cell computational (dry) model, we can have a complete view of how modules act together as a system, and a quantitative visualization of the dynamical behavior of our sensor, high pass filter and quorum sensing system.
| $$X_{FadR}=FadR\times (\frac{\beta^{n2}_{FadR}}{FA^{n2}+\beta^{n2}_{FA}})$$ | {\beta^{n1}_{FadR}+X^{n1}_{FadR}})-\gamma_{TetR_{1}}\times TetR_{1}$$ | $$\frac{\text{d}LuxI}{\text{d}t}=\alpha_{LuxI}\times (\frac{\beta^{n1}_{FadR}}{\beta^{n1}_{FadR}+X^{n1}_{FadR}})-\gamma_{LuxI}\times LuxI$$ | $$\frac{\text{d}FadR}{\text{d}t}=\alpha_{FadR}-\gamma_{FadR}\times FadR$$ |
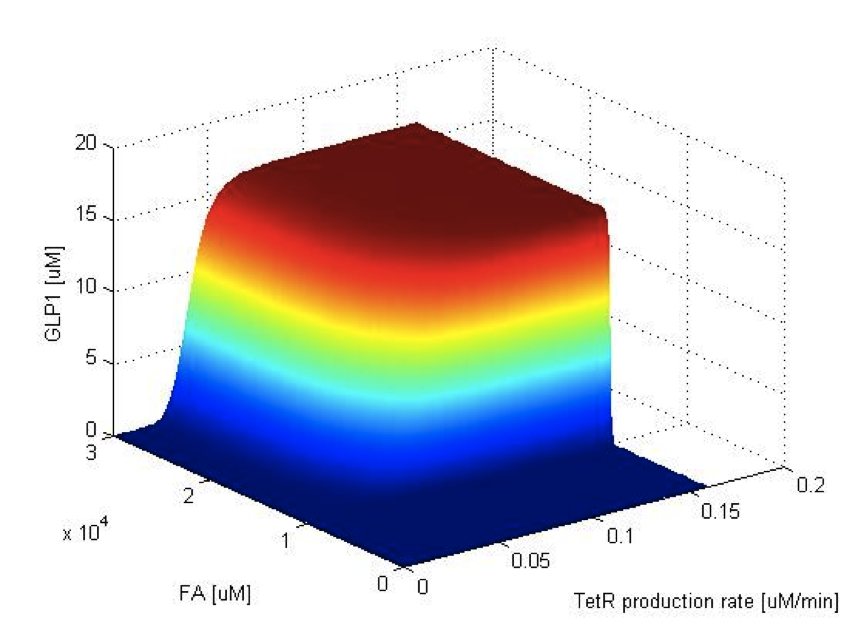
System Analysis
To have better understanding of the roles each parameter plays in our single cell model, we performed system analysis, which explores extensively into the parameter space. With the help from system analysis, we are able to determine which parameters should be adjusted in order to achieve our desired circuit response. This quantitative information will in the future feed into the design and actual construction of our system - for instance, the strength of promoter, copy number of an operator site, degradation rate of a repressor protein, etc.
Cell Population Response Model
To move further from single cell response to the response of a cell population, we conducted another two dimensional spatial-temporal model in COMSOL, which simulate the communication of cells through quorum sensing in our synthetic system.
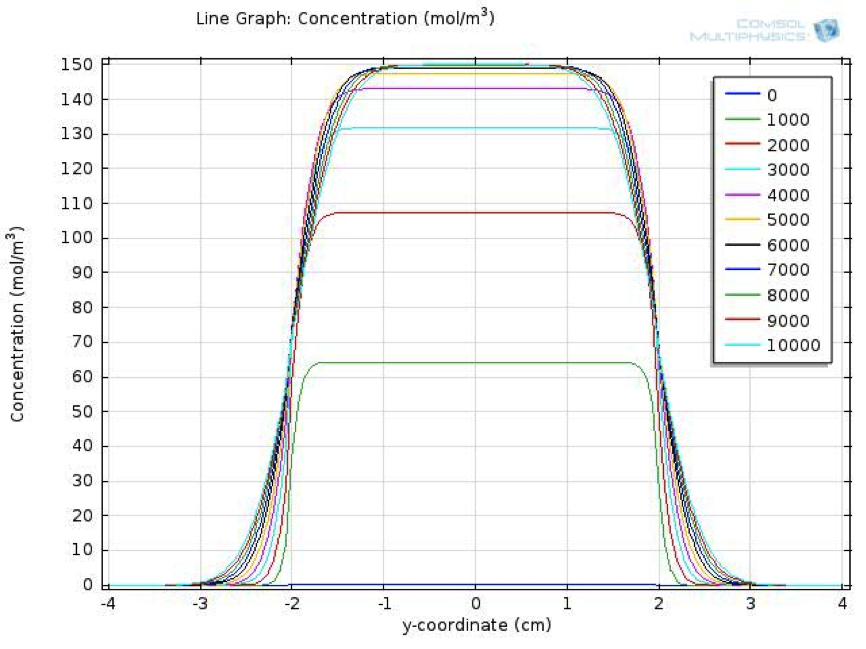
Fatty Acid Reaction Absorption Model
We also created a two dimensional dynamic reaction- absorption model, using the mechanical engineering software platform COMSOL, to describe the spatial-temporal change of fatty acid level in the extracellular environment after a meal.
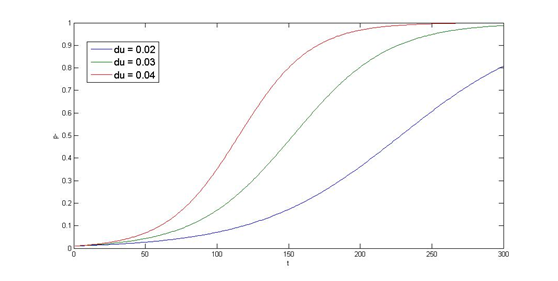
Partition System Model
Last but not least, we performed a simulation of the partition system. As our PepdEx system consists of several plasmids and will function outside of the laboratory (human gut) which lacks of antibiotic selection pressure, plasmid segregation stability is critical that determines whether every single E. Coli cell contains the original system with the designated function. Inspired by natural plasmid & mobile gene element, we cope with segregation instability by incorporating three modules, i.e. partition system, Multimer resolution system and toxin antitoxin system, on top of our system. Choosing which module to stabilize the system needs modeling and stability assay, at this section, we will use cooper’s model as an example.
Overall, we think that modeling was valuable to the decision process in constructing our synthetic network. With the communication between the biologists and modelers, we will be able to, from a simulation result, guide experimentalists in choosing a ‘part’ with appropriate parameter sets (e.g. promoter strength, protein degradation rates) from the sea of iGEM registry, and provide quantitative insights to our flexible and expandable PepdEx system.
 "
"