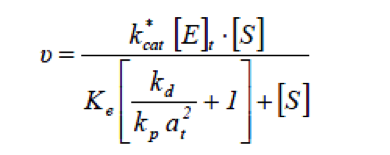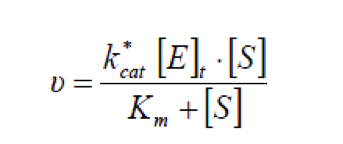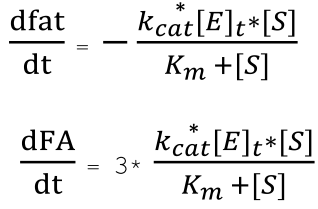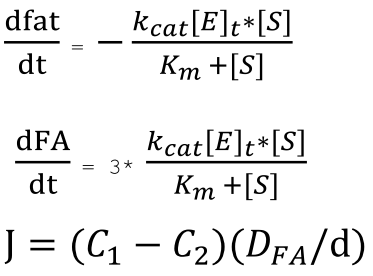Team:NTU-Taida/Modeling/FA
From 2012.igem.org
(→Combined Reaction-absorption Model) |
(→Combined Reaction-absorption Model) |
||
| Line 57: | Line 57: | ||
[[FIle:NTU-Taida-Model-FA-eq4.png|center|300px]] | [[FIle:NTU-Taida-Model-FA-eq4.png|center|300px]] | ||
| + | |||
where C<sub>1</sub> and <sub>C2</sub> are the concentration of the acid in the bulk phase and at the aqueous-lipid interface, respectively. D is the free diffusion coefficient and d represents the thickness of the unstirred water layer. | where C<sub>1</sub> and <sub>C2</sub> are the concentration of the acid in the bulk phase and at the aqueous-lipid interface, respectively. D is the free diffusion coefficient and d represents the thickness of the unstirred water layer. | ||
Revision as of 04:00, 27 September 2012
Fatty Acid Reaction Absorption Model
Overview
With the single cell model, we are able to simulate the response time of our system after the concentration of fatty acid exceeds our filtering threshold. However, the overall response time is also determined by the time needed for the eaten fat to be hydrolyzed and produce a fatty acid concentration higher than the threshold.
Furthermore, since E.coli cells reside mainly on the intestinal walls instead of in the lumen, we have to determine the actual concentration of fatty acid around the intestinal wall, which is different from that in the lumen space. Therefore, we performed a simulation to model the hydrolysis of fat by lipase into glycerol and fatty acids. In parallel, we investigated the mechanism of long chain fatty acid absorption and constructed a two dimensional spatial-temporal model with COMSOL Multiphysics. Finally, we incorporate the reaction of fat hydrolysis into our spatial-temporal model describing fatty acid absorption and therefore result in a combined model simulating the reaction and absorption of fatty acid around the intestinal wall.
Reaction Model
Background
We start our effort for simulating the hydrolysis of fat by determining the rate of fat hydrolysis when catalyzed by lipase.
Lipase catalysed reaction take place at the interface between the aqueous phase containing the enzyme and the oil phase, therefore the rate of hydrolysis by lipase will depend on the total specific interfacial area.[1] When considering systems in which the total specific interfacial area changes with changes in operating condition, the rate of fat hydrolysis can be given by
- at
- Total specific interfacial area [m-1]
- kcat*
- Catalytic rate constant [min-1]
- [E]t
- Total active enzyme concentration [kLU m-3]
- kd
- Desorption rate constant [min-1]
- kp
- Adsorption rate constant [m2 min-1]
- Ke
- Equilibrium constant of ES [mol m-3]
- [S]
- Substrate concentration [mol m-3]
- 𝜈
- Reaction rate [mol m-3 min-1]
When considering a stable system aided by emulsification reagent, the total free interfacial area will be nearly constant and therefore can result in a more simple equation, which is actually in the form of the Michaelis-Menten kinetic equation[2].
Considering the effect of bile acids as emulsification reagents, we used the latter form in our model, with parameters derived from literature[1][2][3].
Equations
Since one molecule of fat will produce three molecules of fatty acids when hydrolyzed, we have the relationship between the rate of reduction of fats and the rate of production of fatty acids, and are able to derive the ODEs describing the change in concentration of fat and fatty acid over time.
Results
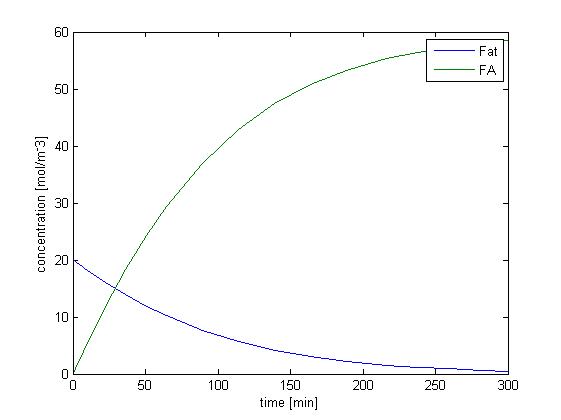
We solved the ODEs above by the Matlab solver with initial concentration of fat as 50mM, and obtain the following result.
Figure 1 shows the dynamic change of concentration of fat and FA over time when lipase catalyzes the hydrolysis of fat. Since our sensing threshold is only about 0.7 mol/m3, it takes very little time for fatty acid to reach our threshold level.
Without considering the absorption of fatty acid, the rising of the concentration of fatty acid is quite fast, and therefore the response time would not be limited by the process of fat hydrolysis but by the process of GLP1 synthesis, which is described in single cell model.
Combined Reaction-absorption Model
Fatty acid absorption takes place on the intestinal walls. This absorption process may generate a concentration gradient near the walls where E.coli cells mainly reside. To more accurately simulate the actual fatty acid concentration in the microenvironment of our E.coli cells, we consider the effect of the absorption process and construct a two-dimensional reaction-absorption model in COMSOL.
The intestinal absorption rate of fatty acid is mainly determined by how fast fatty acid can diffuse through the unstirred water layer and the lipid cell membrane. It has been shown that the rate limiting process in the absorption of short- and medium- chain fatty acid is the diffusion across lipid cell membrane, while the absorption rate of long- chain fatty acid is limited by the diffusion across the unstirred water layer. [4]
Since oleic acid is a long-chain fatty acid, we simulate its absorption by considering the diffusion process across the unstirred water layer, which can be governed by the following equation:
where C1 and C2 are the concentration of the acid in the bulk phase and at the aqueous-lipid interface, respectively. D is the free diffusion coefficient and d represents the thickness of the unstirred water layer.
Spatial-temporal Model Equations
The followings are the equations used in our reaction-absorption model.
Model Design
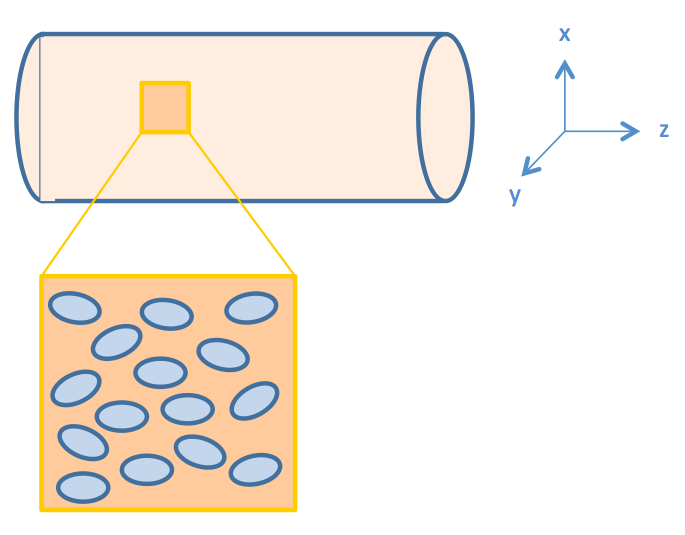
We consider intestinal environment as a cylindrical tube, with cells residing on the walls of the tube, as shown in figure 2.
We assume that the fat distribution in the lumen is uniform and the absorption occurs uniformly along the cylindrical wall. In this way, the distribution of fat or fatty acid would be independent of the z axis. Therefore, we simplified the three dimensional model into a two dimensional one, represented by the cut plane shown in Figure 3.
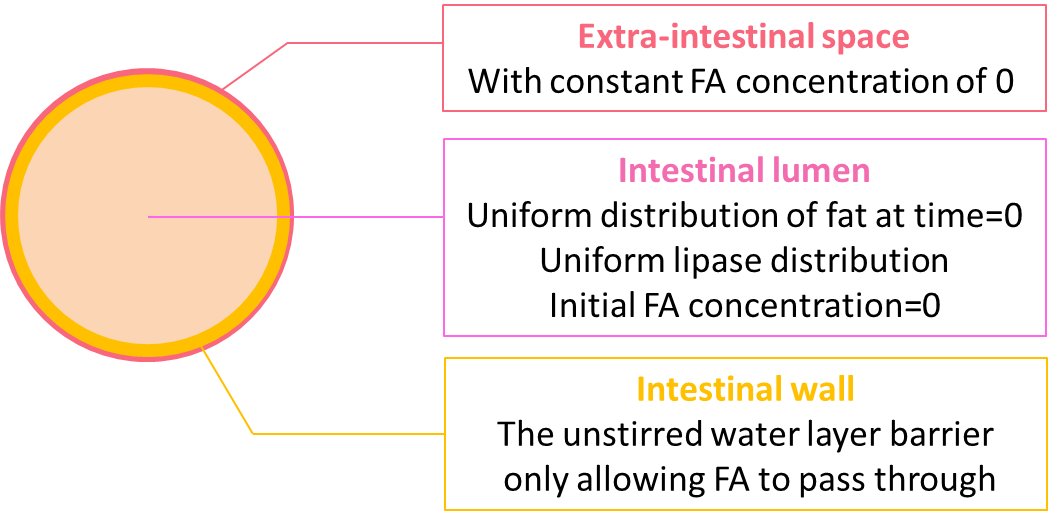
The geometry design of our model is shown in figure 4.
We coupled the ODEs of the reaction model locally at the lumen space, but not in the extra-intestinal space as the fat would only be hydrolyzed in the lumen. On the boundary of the lumen, we incorporate the equation accounting for the diffusion of fatty acid through the unstirred water layer. Initially, there is no fatty acid in either the lumen space or the extra-intestinal space, and the lumen is uniformly filled with fat of 50 mM. As the reaction proceeds, we expect to see the concentration of fat start to decline uniformly regardless of proximity to the perimeter. In contrast, while the concentration of fatty acid starts to rise, the rate of increase is not uniform because of the diffusion through the unstirred water layer.
Results - Animations showing the spatial temporal change in concentration of fat and fatty acid
We simulated the concentration of fat and fatty acid for 104 seconds with initial conditions described in the Model design section.
The results are shown in video 1 and 2 for the concentration of fat and fatty acid, respectively. As we expected, the concentration of fat declines uniformly in the lumen and the concentration of fatty acid rises but with the presence of non-uniform distribution near the unstirred water layer barrier.

| 
|
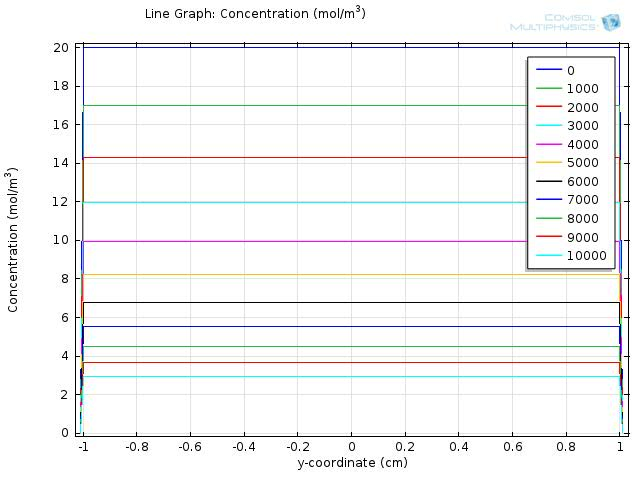
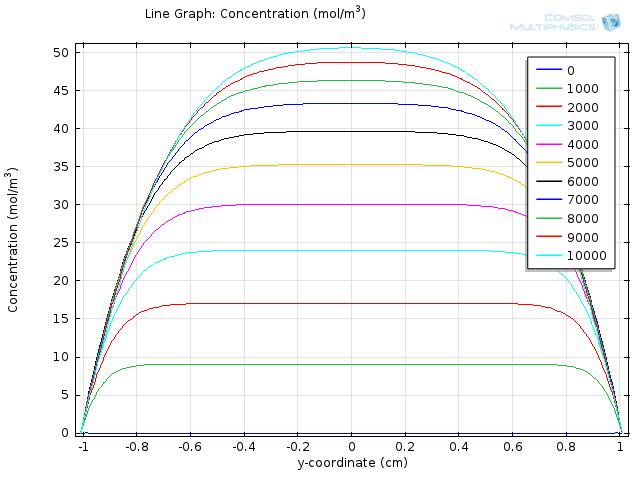
To gain further insights into our simulation results, we plot the concentration of fat and fatty acid along the diameter of the circle. The results for fat and fatty acid are shown in Figure 5 and 6, respectively.
In the figures, curves with different colors represent the concentration along the cut line at different time, with the numbers in the legend showing the time in seconds. The water layer barriers locate at y-coordinate of -2 and 2, respectively.
From Figure 5, we see that the concentration of fat falls uniformly within the y-coordinates of -2 and 2, and remains at zero outside of the lumen space.
In Figure 6, we can see that as the time increases, the overall concentration of fatty acids increase dramatically, but with the central plateau becoming thinner and thinner due to absorption at the unstirred water layer.
Within the time span of simulation, which is 104 seconds, the concentration of fatty acid near the water layer barrier remains much lower than that of the central part, but still reaches about 30 mM at 1000 seconds and continues increasing with time.
Therefore, although the concentration of fatty acid near the intestinal walls is quite different from that of the lumen space, the concentration still exceeds our sensing threshold quickly, which enables our system to sense the fat intake event rapidly and start our circuit in time.
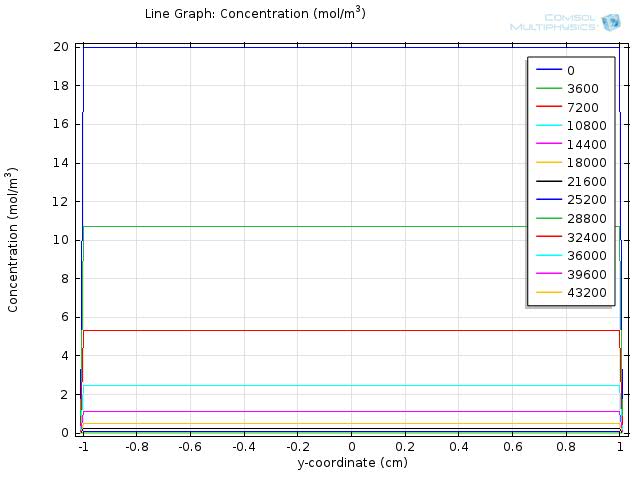
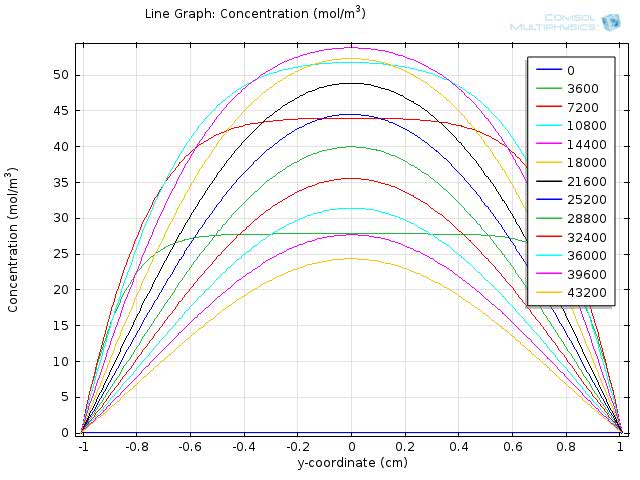
Simulation for longer time span
As the fat is completely hydrolyzed at time=104 seconds,we expect the difference in concentration between the intestinal lumen and walls to decrease as the simulation goes on. We show the results for simulating the concentration of fatty acid for 105 and 106 seconds in Figure 7 and Figure 8, respectively, and video 3 further documents the change of concentration over 106 seconds. The results are as we expected, when time exceeds 104 seconds, the difference in concentration between the intestinal lumen and walls starts to decrease and is finally eliminated at a time of about 7*105 seconds.

Reference
- Kinetics of the enzymatic hydrolysis of palm oil by lipase
- Kinetics of hydrolysis of tributyrin by lipase
- http://journals.lww.com/pancreasjournal/Documents/pancreas%20chapters/the%20pancreas%20Ch23.pdf
- Determinants of intestinal mucosal uptake of short- and medium-chain fatty acids and alcohols.
 "
"