Contents 1 Why Modelling?: 2 Model Overview: 2.1 Model Application 2.2 What´s inside the box? 3 Extended Model 4 Applying the model: Synechocystis promoters

Why Modelling?:

Synechocystis transcriptional circadian oscillation makes it an exceptional chassis if time control of synthetic metabolic processes is desired. Nevertheless, the functionality of some of these processes depends upon precise timing. While there are hundreds of genes known to oscillate in Synechocystis genome -each with its own peak, strenght and amplitude- it can be tricky to choose the right ones. Here is where our modeling approach comes on stage.

Model Overview:

Model Application

Our model works as a user-friendly black box. The user´s input is the desired time of protein concentration peak and the program´s output is a list of suggested promoters. It can be adjusted to take as input the time on which enzymatic products concentration peaks , or to maximize an intermediate metabolite that depends not just on production but also consumption. Finally, its logical design can be applied to any other organism that exhibits circadian oscillation.

What´s inside the box?

We took all the microarray data available of promoter of Synechocystis grown on normal conditions. Conveniently, these arrays already have a filter: they only contain cycling promoters

The microarray data points were adjusted by a least squares algorithm into sine functions for each promoter.

Where k, theta and y are parameters to adjust. x is protein concentration

This equation accounts for protein production and its included into this form of universal balance equation:

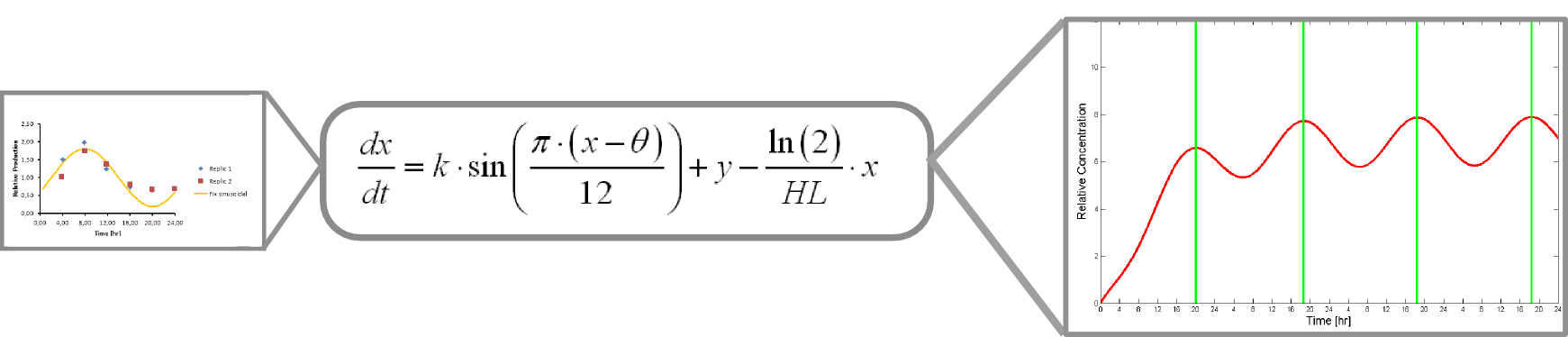
Where HL is protein´s half life

The resulting plot of this equation predicts protein concentration over time.

As a complement, we developed a list of relative promoter strengths. We took one promoter present in all datasets to make a relative scale, then, we transformed it to an absolute scale using a promoter quantitatively characterized in literature by comparing it to the relative scale promoter.

Extended Model

The approach can be extended to consider as input the product of the protein enzymatic activity instead of the protein itself.

Moreover, it can be adjusted to a two-protein model in which protein 1 produces the metabolite and protein 2 consumes it.

Applying the model: Synechocystis promoters

We applied our model to solve the question of which promoters should we use to meet our strategy (https://2012.igem.org/Team:UC_Chile/Cyanolux/Project_short#Strategy) goals

The results are shown below:

Why?

To express bioluminescence under circadian oscillation it was essential to identify the ideal promoters that could yield highest substrate concentrations at the exact time our biolamp is on i.e. by night.

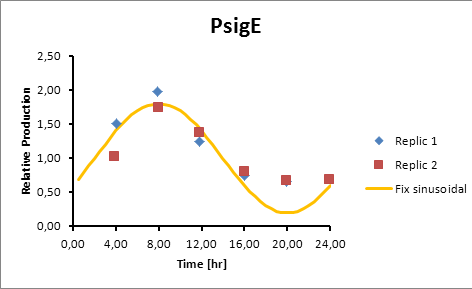
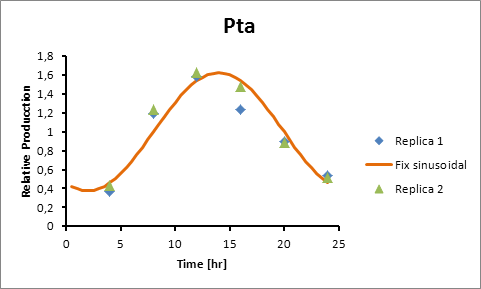
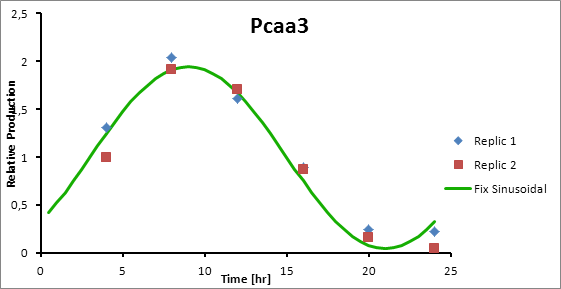
Based on literature (ref) we found that suitable promoters to start our model were sigE (sll1689), Transaldolase (slr1793) and Cytochrome aa3 (sll1898).

Therefore, in the following section we explain how to model the oscillation in terms of product generation under three circadian promoters: sigE (sll1689), Transaldolase (slr1793) and Cytochrome aa3 (sll1898).

Methodology

Product generation by promoter

From known sigE (sll1689) production data we could build up a model using MatLab software. (Please check our script!).

Basically, what we have after data adjustment is a sine function consistent with the oscillatory nature of the circadian rhythm.

Generation = C*sen(2π(t-(peak-6))/12)+1

The C parameter was optimized using Excel Solver’s algorithm of least squares.

For Transaldolase (slr1793) and Cytochrome aa3 (sll1898) a microarray data was adjusted (using the same algorithm of least squares) to obtain:

Promoter Peak hour PsigE 8 Pta 14 Paa3 9

So, the protein generation models for each of the promoters are:

sigE production=0,8028*sen(π(t-2)/12)+1

Pta production=0,6246*sen(π(t-8)/12)+1

Pcaa3 production=0,9493*sen(π(t-3)/12)+1

Solving ODE’s

Assumptions: reaction only depends on promoter activity. Protein half life expression of 8 hours.

LuxAB concentrations

We start with the fundamental balance law:

Entries-exits+generation-consumption= accumulation

As there is no entries nor exits (closed system) the expression becomes

Generation-consumption= accumulation

For LuxAB we know

Generation= k_1*sen((π*(t-8))/12)+1 (obtained above)

Consumption=ln(2)/t_m *X(t)

Equation to solve

dX/dt=k_1*sen((π*(t-8))/12)+1-ln(2)/t_m *X(t)

Using Matlab to solve this ODE

For LuxCDEG

Generation=k2*sen((π*(t-2))/24)+1

Consumption=ln(2)/t_m *Y(t)

Equation to solve

dY/dt=k_1*sen((π*(t-8))/12)+1-ln(2)/t_m *Y(t)

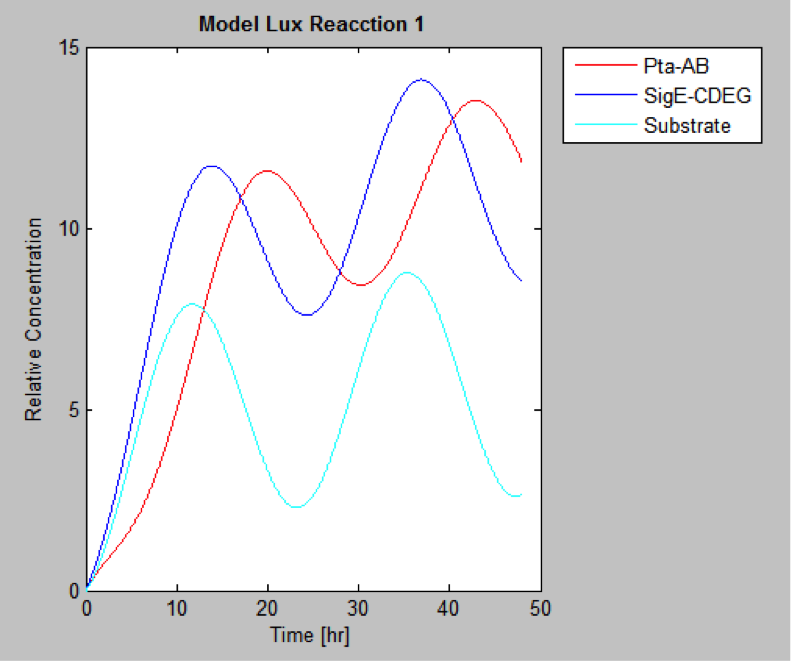
MatLab result

Finally we have the protein concentrations at different times

The files for the following models are:

Digitize2.m UC-chileDiffs.m

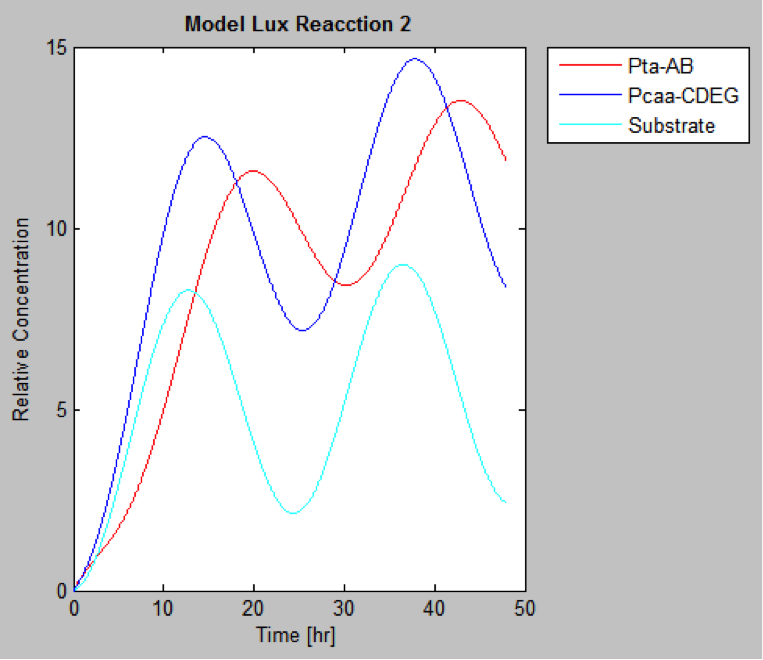
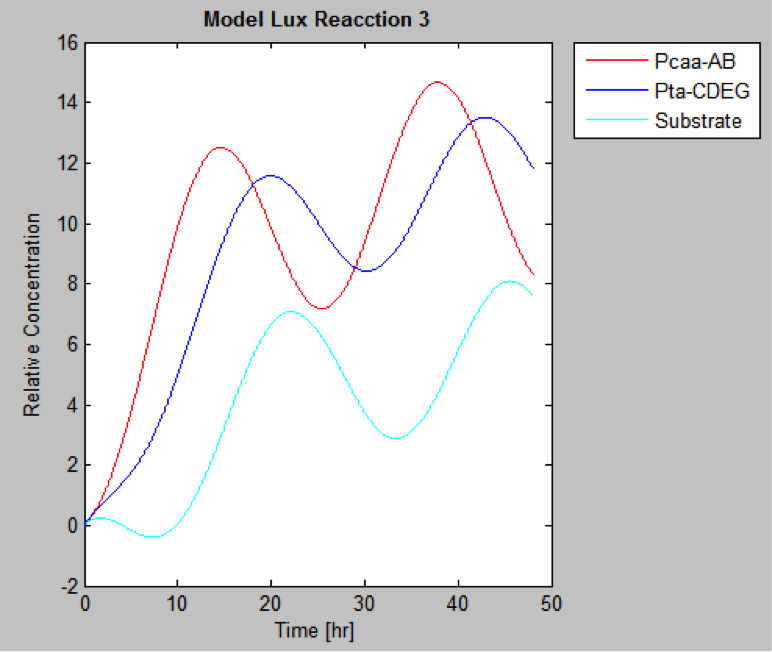
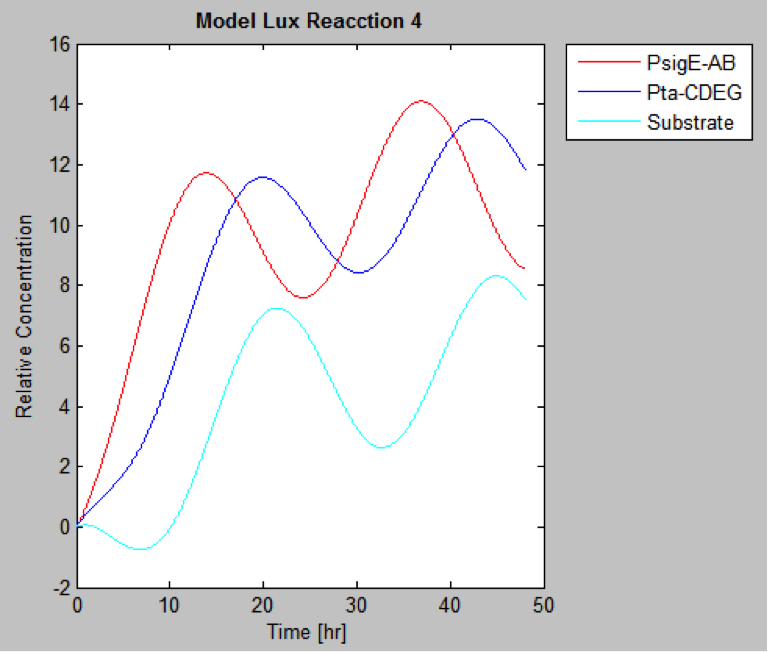
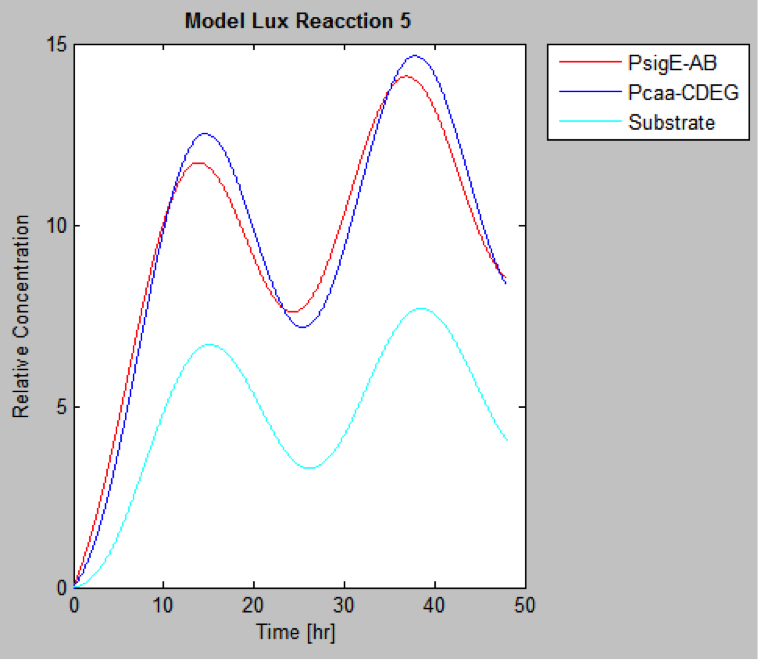
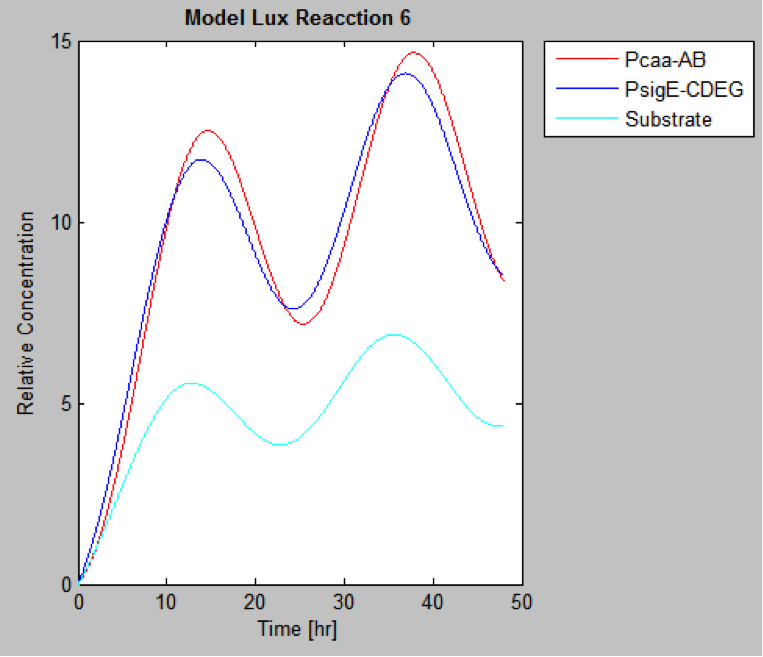
The following are the models we obtained by MatLab

And this is the best model because it yields highest substrate concentration at the desired time (12 hr)