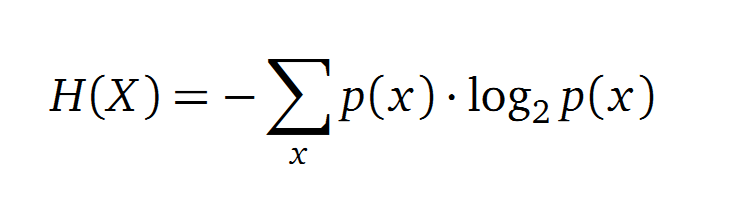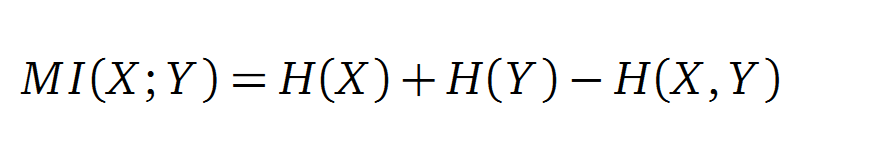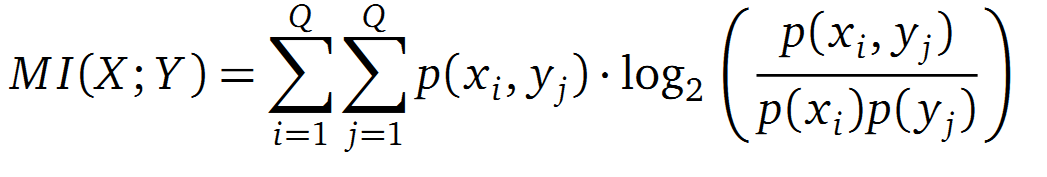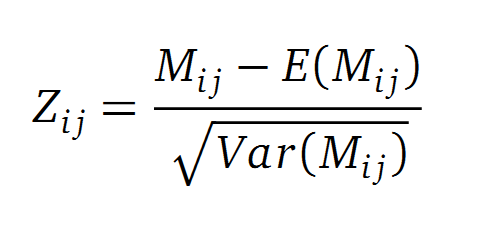Team:TU Darmstadt/Modeling IT

Homology Modeling |	Gaussian Networks |	Molecular Dynamics |	Information Theory |	Docking Simulation

---

Contents 1 Information Theoretical Analysis 1.1 Information Theory 1.1.1 Entropy 1.1.2 Mutual Information 1.2 Application of MI to sequence Alignments 1.3 Normalisation 1.4 Method 1.5 Results 1.5.1 Fs. Cutinase 1.5.2 PnB-Esterase 13

Information Theoretical Analysis

Information Theory

Entropy

Claude Shannon created a measurement approach of uncertainty of a random variable X. This measurement is called Shannon entropy H [1] which is measured in bit, if a logarithm to the base 2 is used. p(x) denotes the probability mass function of a random variable X.

Mutual Information

In information theory, Mutual information (MI) measures the correlation of two random variables X and Y. H(X) and H(Y) are the Shannon entropies of the random variables X and Y. H(X,Y) is the joint entropy of X and Y. In other words, the MI quantifies the amount of information of variable X by knowing Y and vice versa.

Application of MI to sequence Alignments

It is well known that the MI can be used to measure co-evolution signals in multiple sequence alignments (MSA)[2] [3] . An MSA serves as a comparison of three or more sequences used to investigate the functional or evolutionary homology of amino acid or nucleotide sequences. The MI of an MSA can be computed with the following equation derived from the Kullback-Leibler-Divergence (DKL):

with p(x) and p( y) being the frequency counts of symbols in column X and Y of the MSA. The joint frequency describe the occurrence for the amino acids xi and yj(p(x, y)) and Q is the set of Symbols derived from the corresponding alphabet (DNA or Protein). The result of these calculations is a symmetric matrix M which includes all combined MI values for any two columns in an MSA. A dependency of two columns acids shows high MI values.

Normalisation

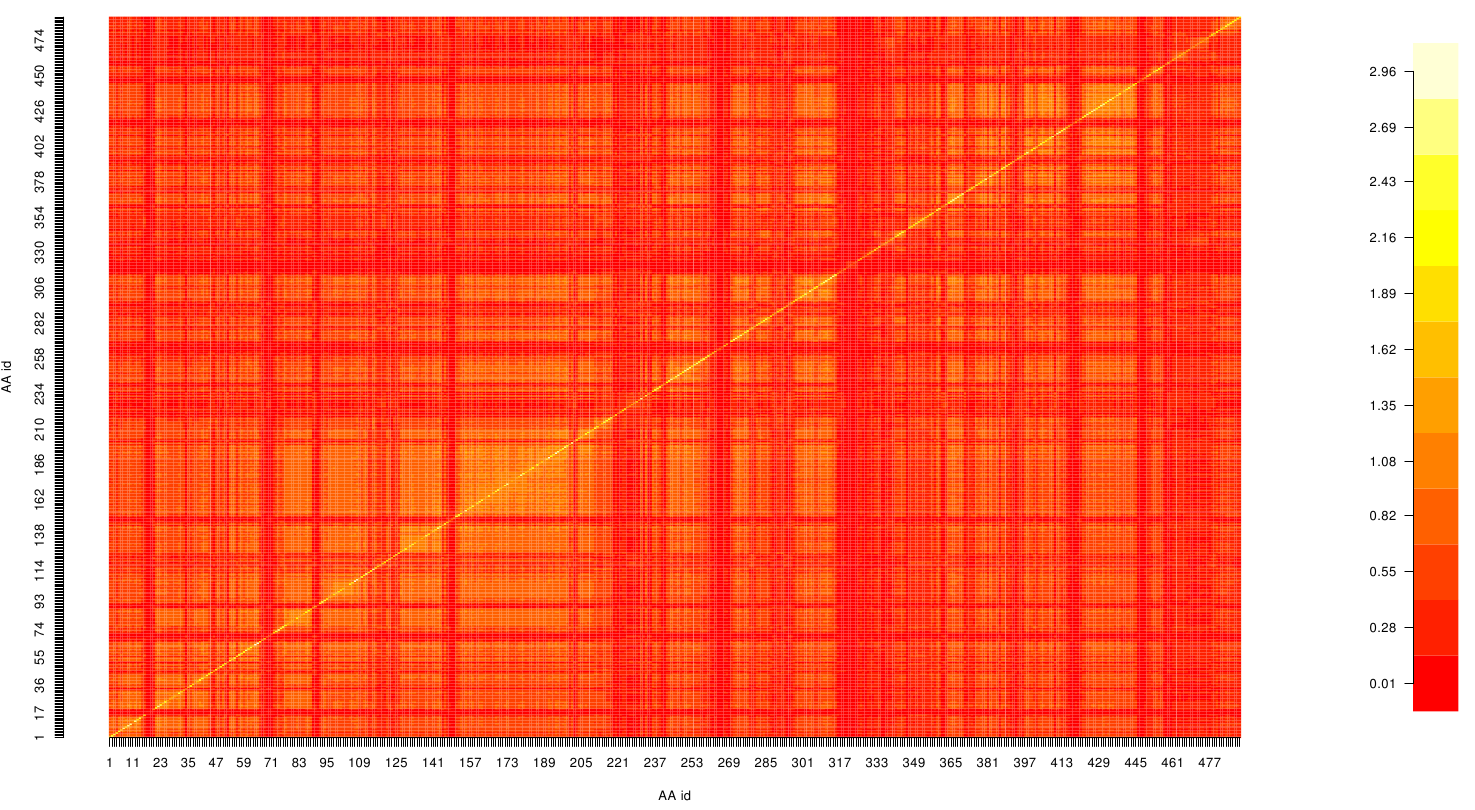
A standard score (Z-score) indicates how many standard deviations a value differs from the mean of a normal distribution. MI dependent Z-scores can be calculated with a shuffle-null model, where the symbols in MSA column are shuffled and every dependencies of the column pairs are eliminated. The expectation value for the shuffle-null model is described by E(Mi j) and its corresponding variance by Var(Mi j) [4].

Method

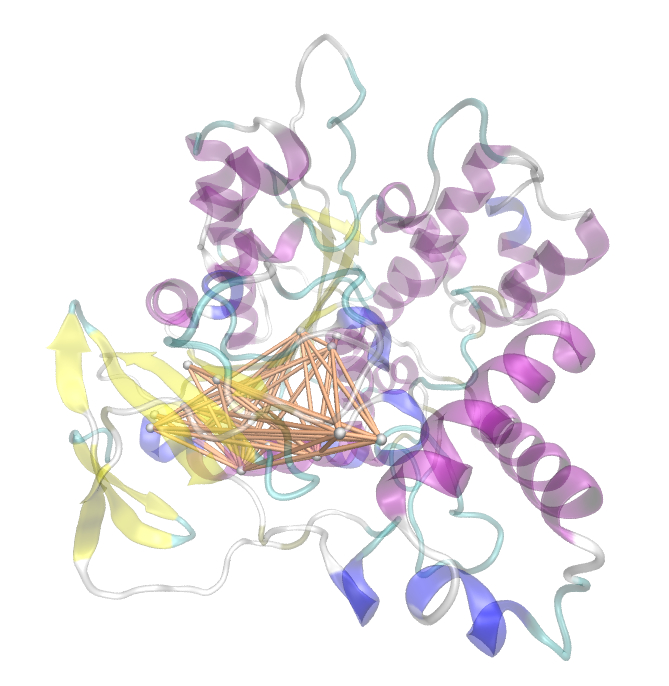
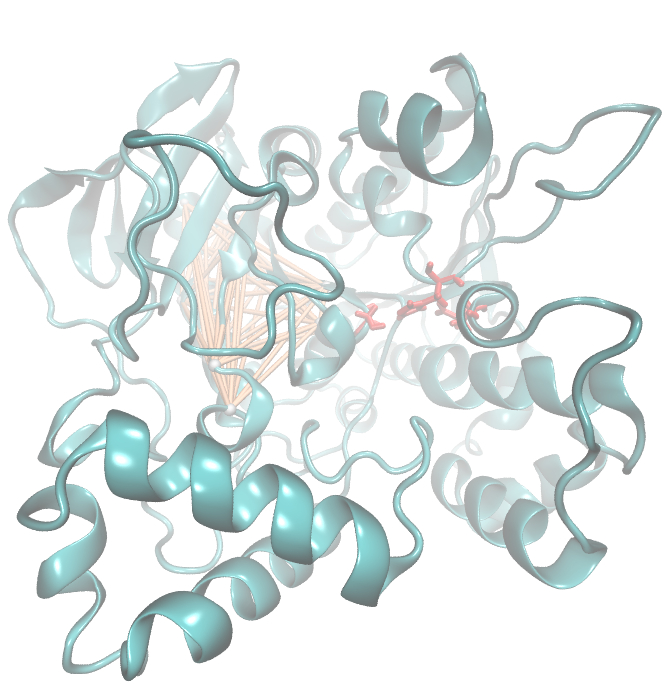
Due to the the information theoretical analysis we are able to optimize our enzymes. Nevertheless, we have to create sequence alignments with an satisfying size. We obtained our sequences from the National Center of Biotechnological Information database (NCBI) using the Basic Local Alignment Search Tool (BLAST). Hence we used an e-value cut-off of 10^5. Since we collected the sequences we used clustalo for the alignment creation. The entropy and MI calculations were performed with R using the BioPhysConnectoR library.

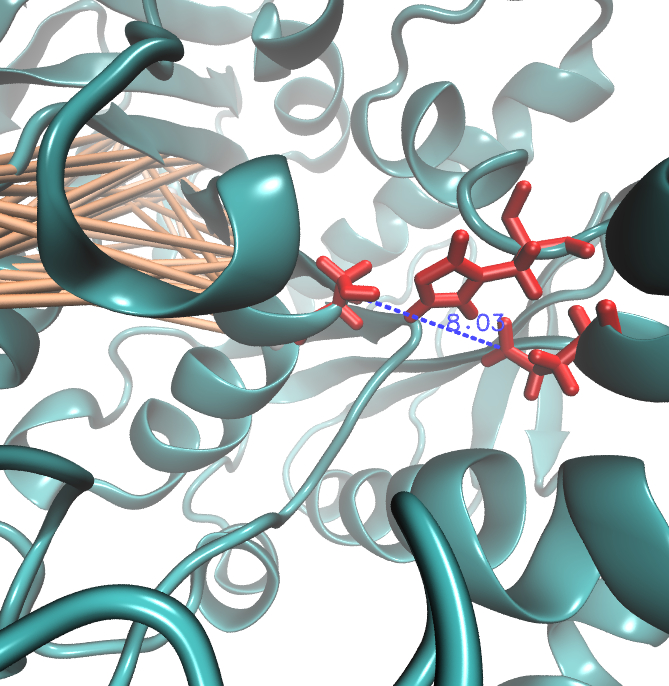
Results

Fs. Cutinase

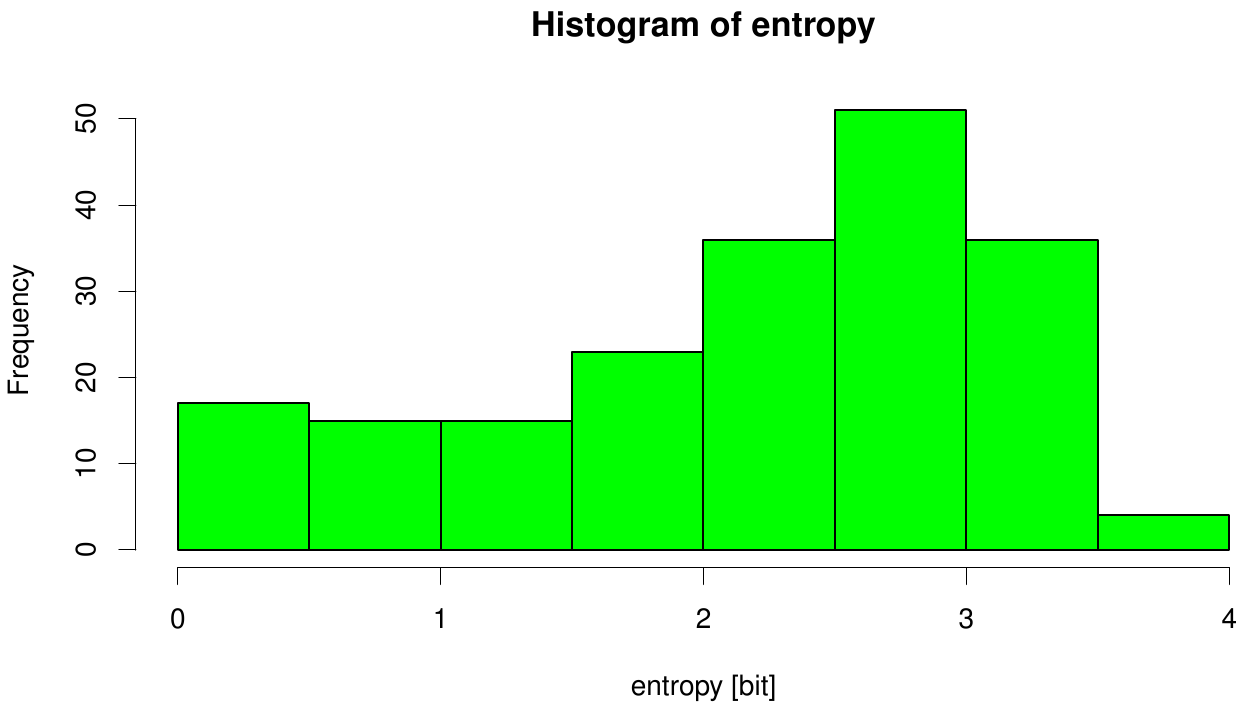
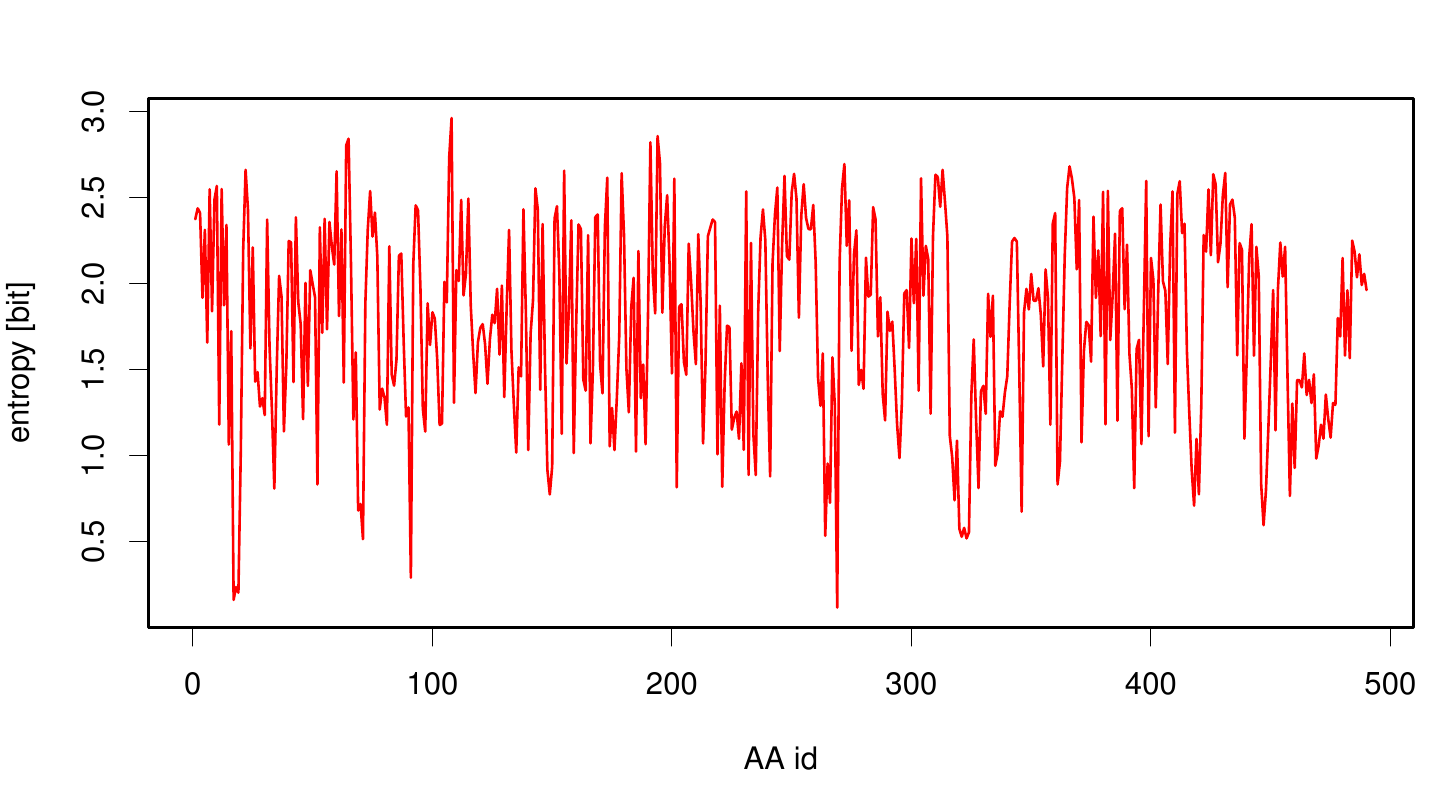
We utilized the entropy as a measure to detect evolutionary stable or conserved positions in sequence alignments. Moreover, these positions are considered to be essential for the stability or function of the protein.

Here we illustrate an histogram of entropy values derived from our Fs. Cutinase alignment. Hence we can observe that the largest amount of entropy values are within a binning of 2 and 3.

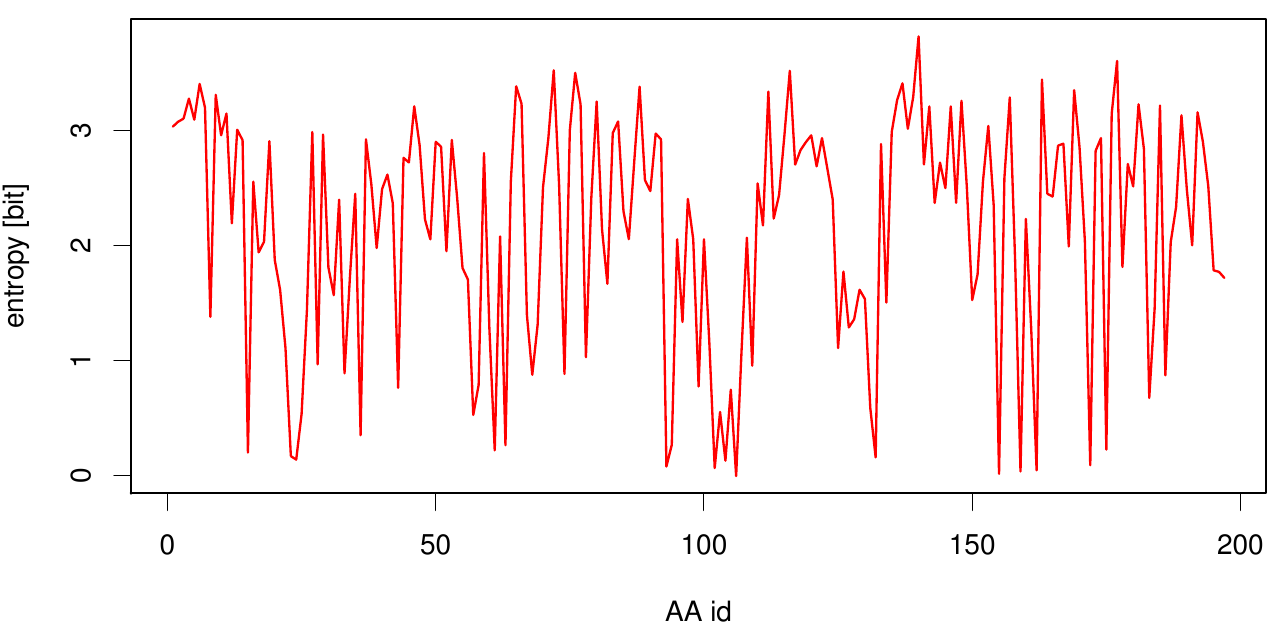
Here we show the entropy as a function of time.

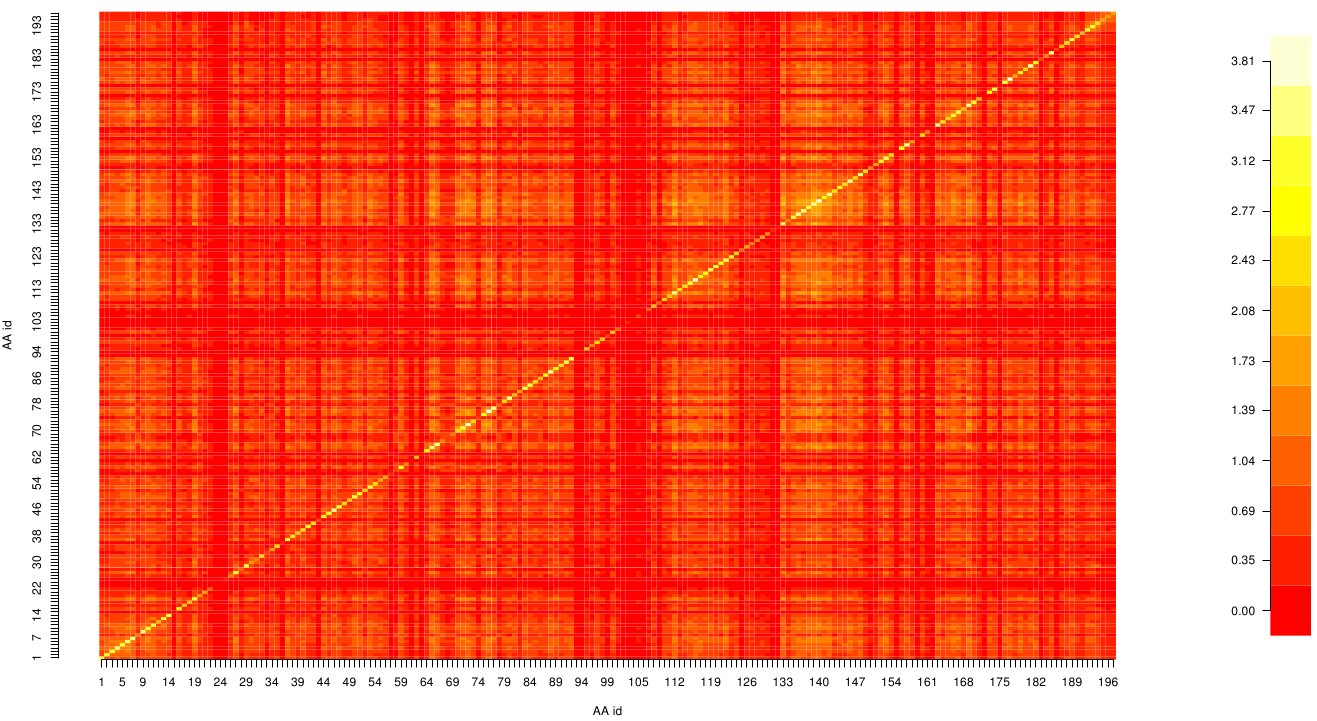
Here we show the Z-score matrix as a heat map representation.

PnB-Esterase 13