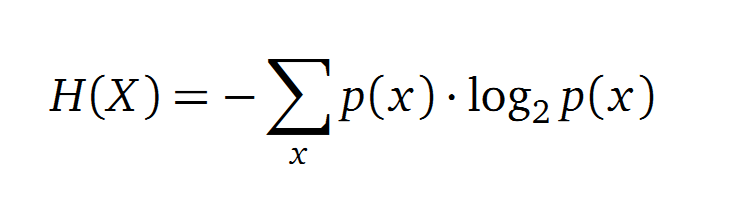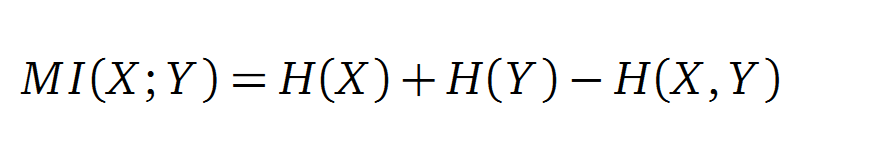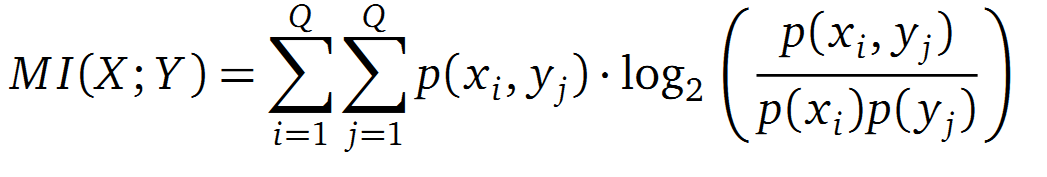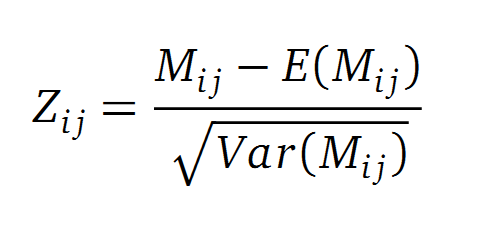Team:TU Darmstadt/Modeling IT
From 2012.igem.org
| Homology Modeling | | Gaussian Networks | | Molecular Dynamics | | Information Theory | | Docking Simulation |
|---|
Contents |
Information Theoretical Analysis
Information Theory
Entropy
Claude Shannon created a measurement approach of uncertainty of a random variable X. This measurement is called Shannon entropy H [1] which is measured in bit, if a logarithm to the base 2 is used. p(x) denotes the probability mass function of a random variable X.
Mutual Information
In information theory, Mutual Information (MI) measures the correlation of two random variables X and Y. H(X) and H(Y) are the Shannon entropies of the random variables X and Y. H(X,Y) is the joint entropy of X and Y. In other words, the MI quantifies the amount of information of variable X by knowing Y and vice versa.
Application of MI to sequence Alignments
It is well known that the MI can be used to measure co-evolution signals in multiple sequence alignments (MSA)[2]. An MSA serves as a basis to investigate the functional or evolutionary homology of amino acid or nucleotide sequences. The MI of an MSA can be computed with the following equation in form of a Kullback-Leibler-Divergence (DKL):
with p(x) and p(y) being the probabilities of the occurence of symbols in column X and Y of the MSA. The joint probability p(x, y) describes the occurrence of one amino acid pair x i and y j and Q is the set of Symbols derived from the corresponding alphabet (DNA or Protein). The result of these calculations is a symmetric matrix M which includes all MI values for any two columns in an MSA. A dependency of two columns and thus amino acids shows high MI values.
Normalisation
A standard score (Z-score) indicates how many standard deviations a value differs from the mean of a normal distribution. MI dependent Z-scores can be calculated with a null model, where the symbols in MSA column are shuffled and every dependency of the column pairs are eliminated, but the entropy in each column is kept constant. The expectation value for the shuffle-null model is described by E(M ij) and its corresponding variance by Var(M ij) [3].
Method
Due to the the information theoretical analysis we are able to optimize our enzymes. To this end we have to create sequence alignments with a satisfying size. We obtained our sequences from the National Center of Biotechnological Information database (NCBI) using the Basic Local Alignment Search Tool (BLAST) [4]. We used an e-value cut-off of 105. To create an MSA we used the tool clustalo [5]. The entropy and MI calculations were performed with R using the BioPhysConnectoR [6] package.
Results
Fs. Cutinase
Due to the sequence search we collected for the Fs. Cutinase 1076 sequences. After aligning them we are able to calculate entropy and MI and thus z-scores, from this alignment. We utilized the entropy as a measure to detect evolutionary stable or conserved positions in sequence alignments. Moreover, these positions are considered to be essential for the stability or function of the protein.
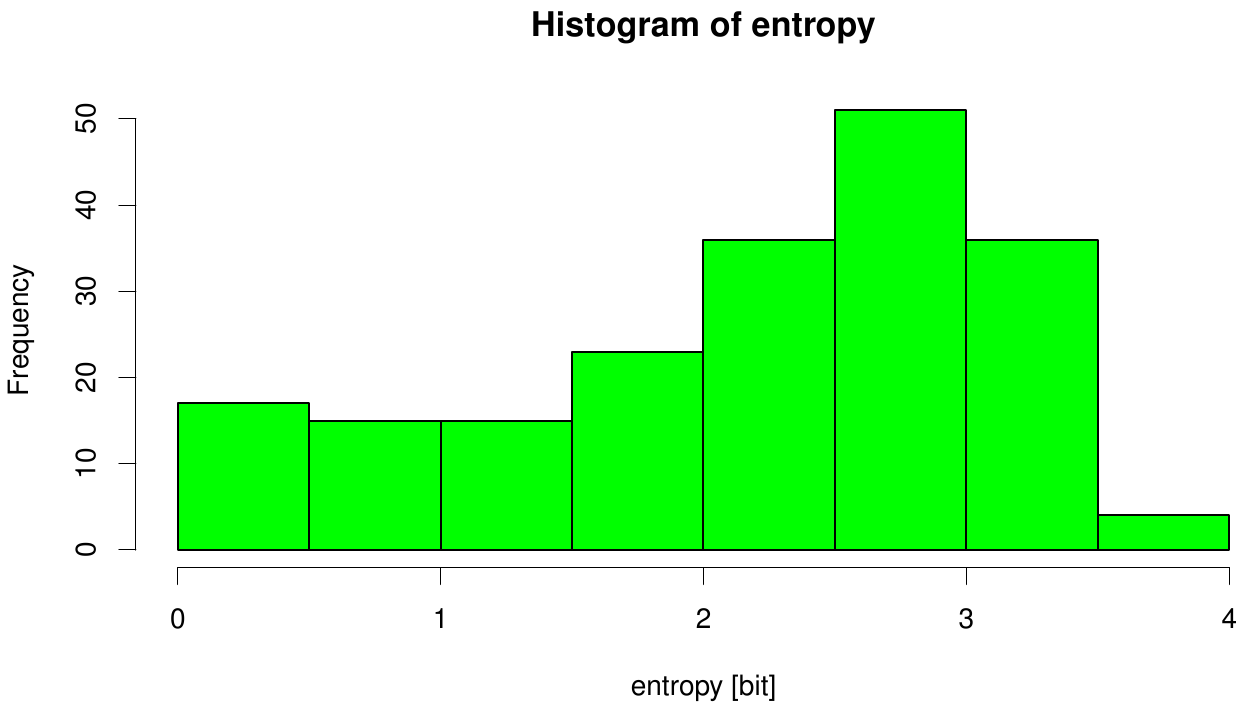
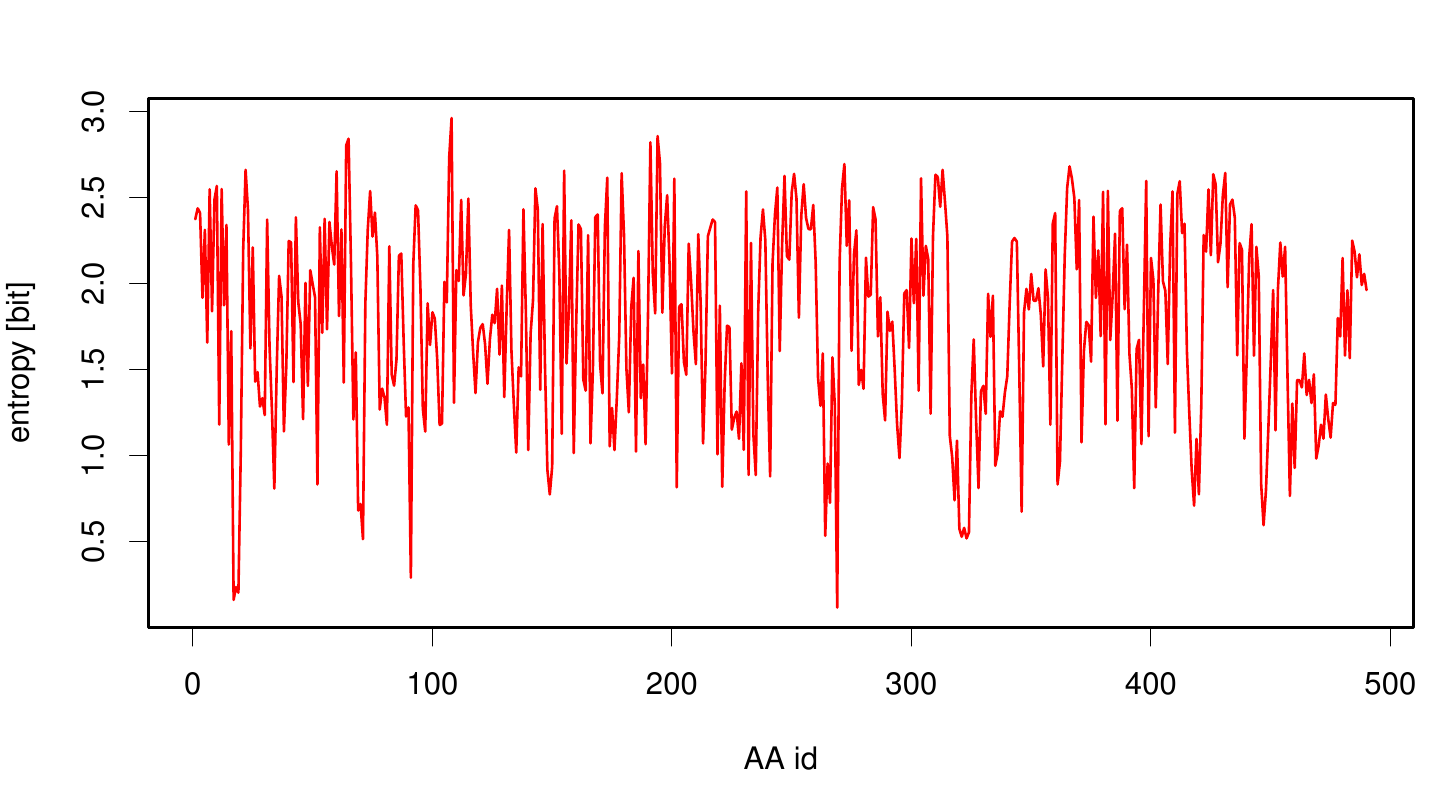
Here we illustrate an histogram of entropy values derived from our Fs. Cutinase alignment. Notably the largest amount of entropy values is within a range from 2 to 3.
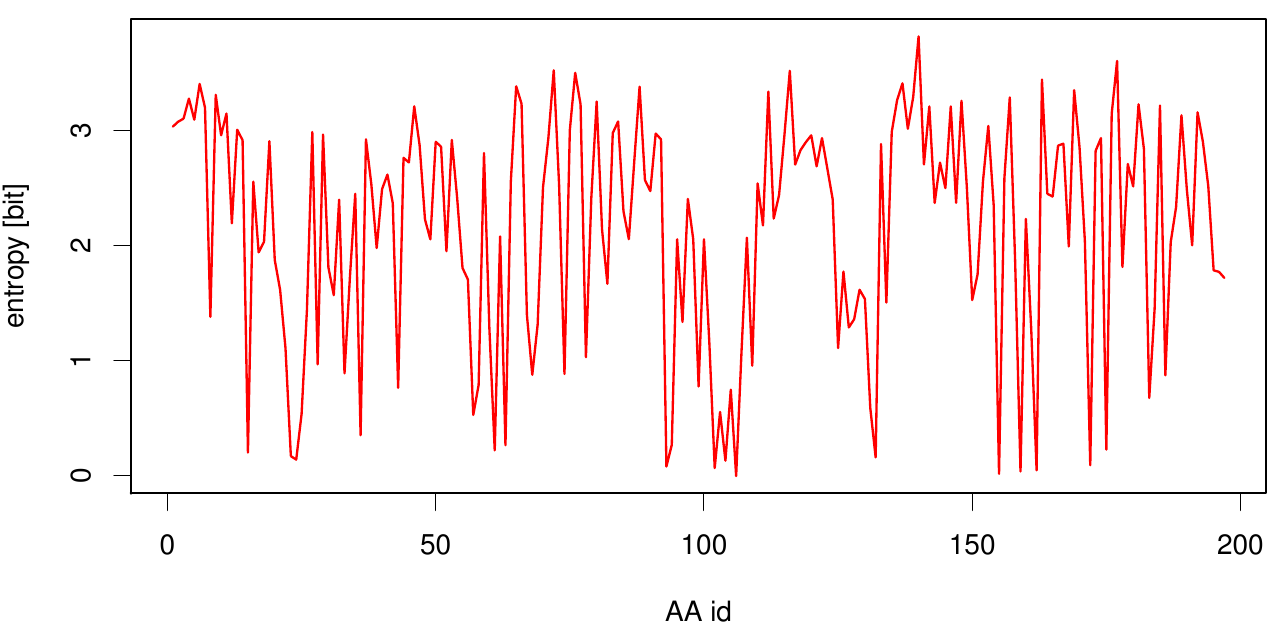
Here we show the entropy as a function of time. Thus we identified the conserved serin-hydrolase motif (ASP, HIS SER) consisting of ASP 175, HIS188 and SER 120, with entropy values of less than 0.2 bit.
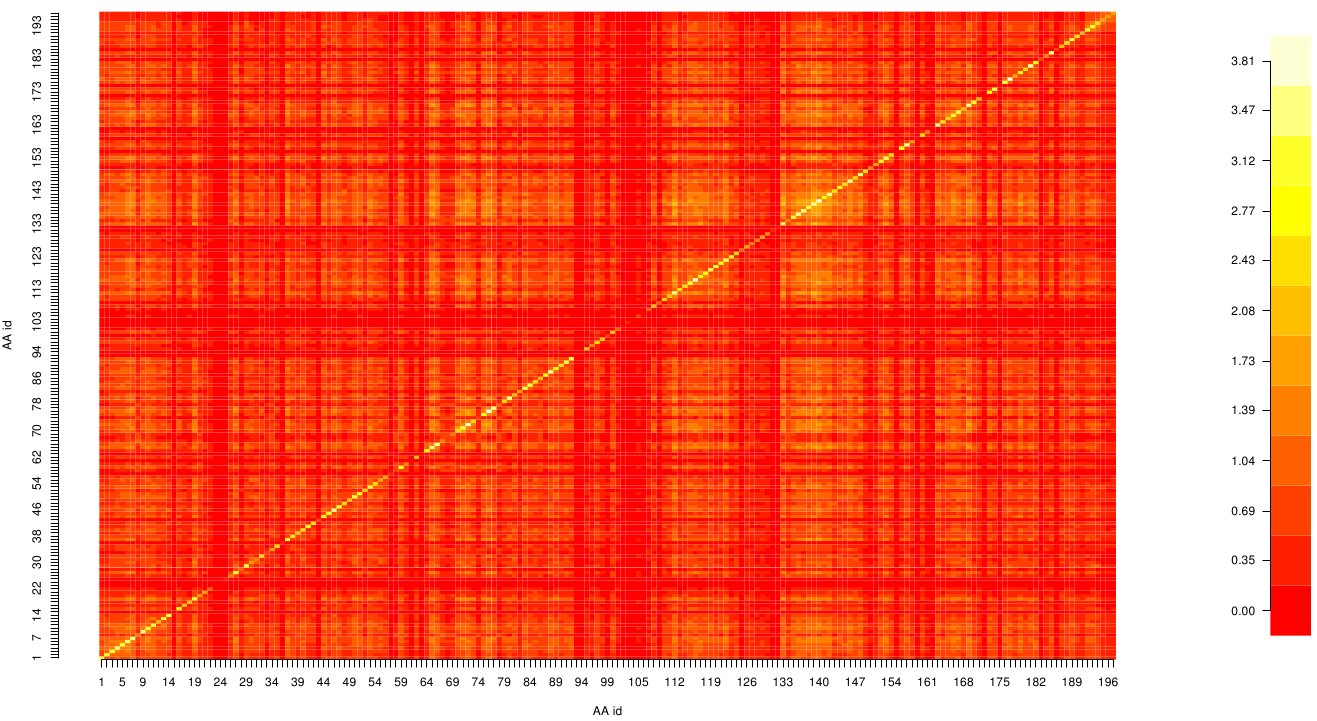
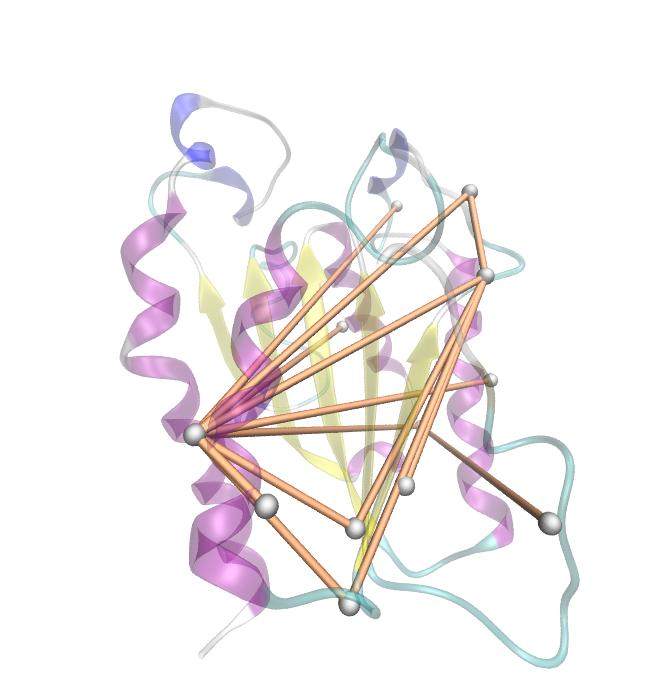
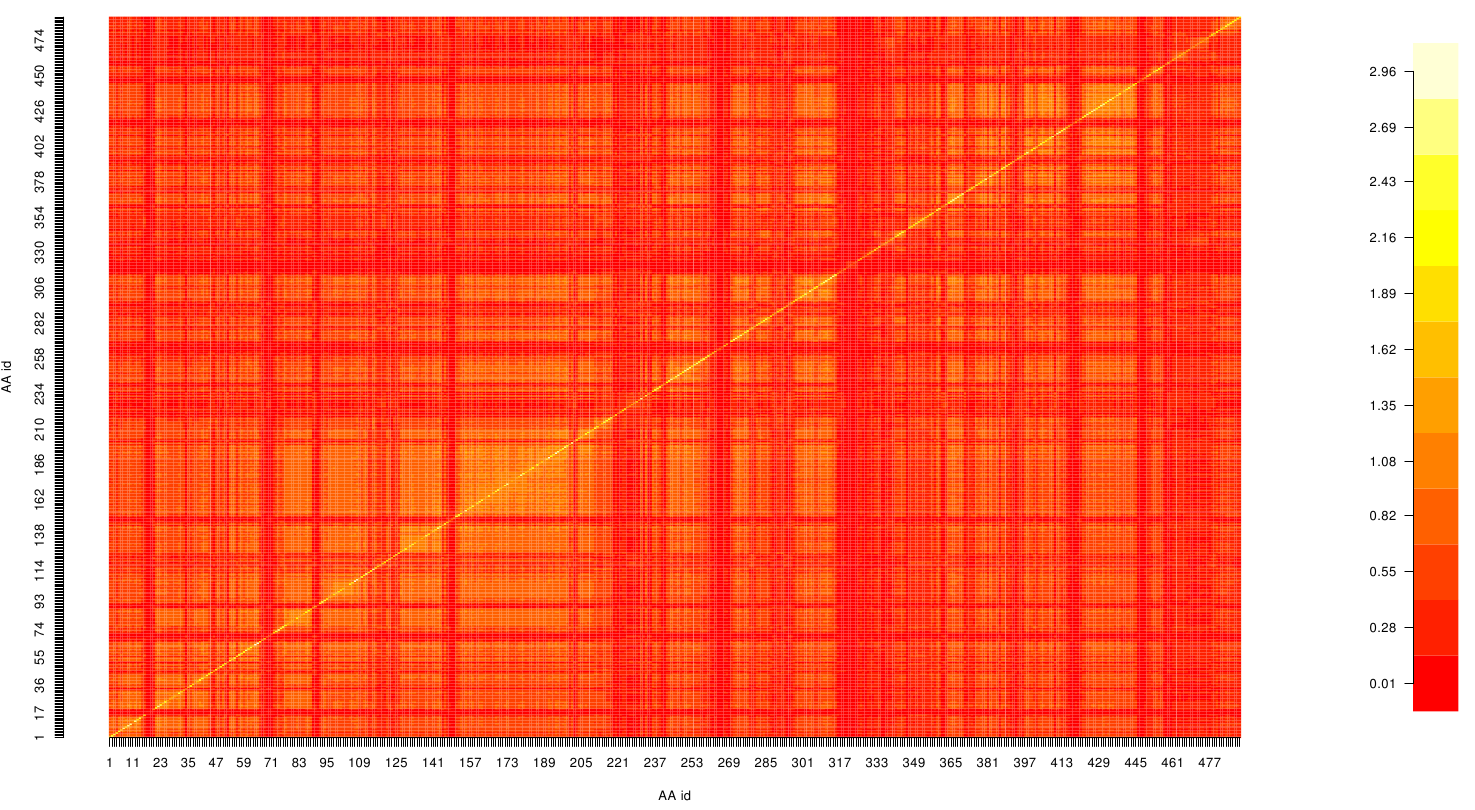
Here we show the MI-matrix as a heat map representation. Hence, we focused on the active site region, where we can observe several regions within MI values of less than 0.3 bit. This seems to indicate non-co-evolving regions or results of a high two-point entropy. In contrast to this, we measured high-scoring MI values around residue THR 74 which seems to co-evolve whith the whole protein.
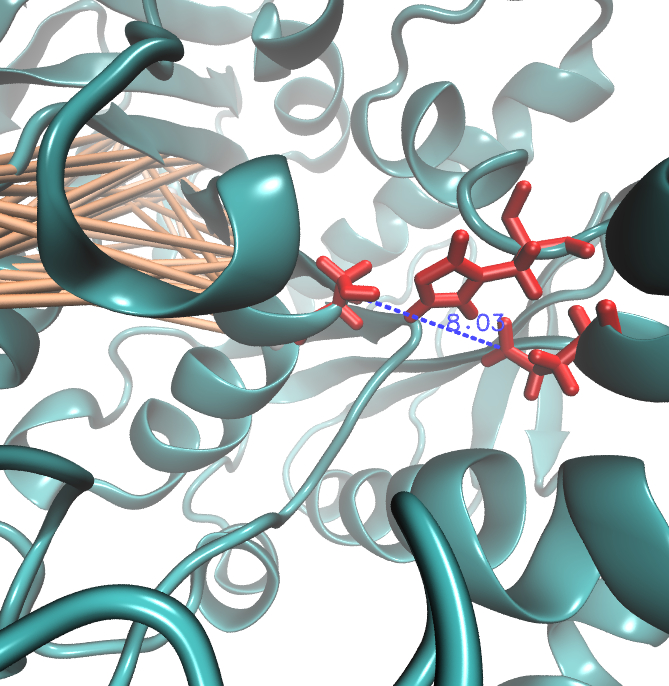
For the illustration of the co-evolving cluster, we highlighted the MI network in the structure above. However the detected residues give hints to the evolutionary correlation of this protein, an experimental proof is necessary.
PnB-Esterase 13
For the pNB-Esterase 13 we obtained 14 943 sequence from NCBI and processed them with clustal omega.
Due to the entropy calculation we identified ALA 17, GLU 18, ASN 19, ALA 91 and PHE 269 as conserved residues.
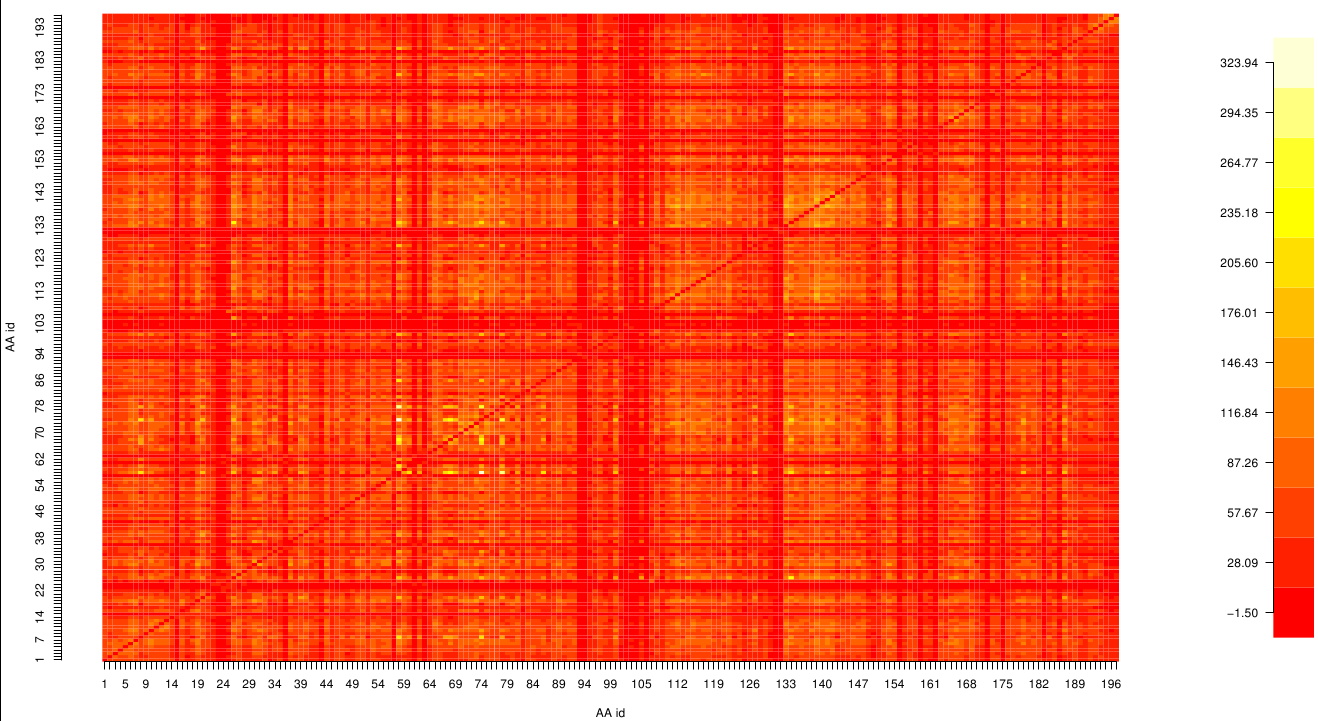
Here we show the MI-matrix (left) and the corresponding z-score matrix (right) as a heat map representation. Thus we identified ASP 159, ARG 135, GLY 140, TRP 166, PHE 174, GLY 176 and GLY 185 as co-evolving residues with the highest values (MI and z-scores).
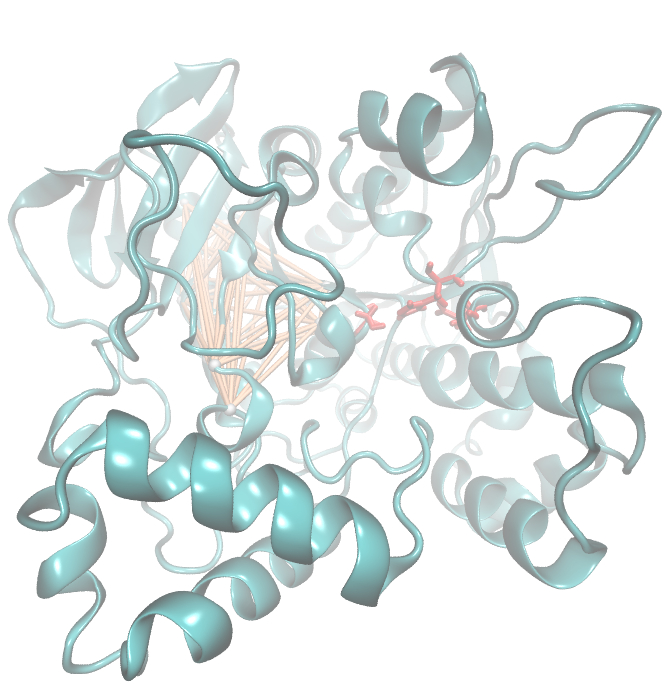
Hence we used the sequence alignment of the pNB esterase 13 to identify the catalytic triad of the serin hydrolase. Similar to other folds it consist of Ser 187, HIS 399, GLU 308. Interestingly, we measured high MI values and z-scores of a cluster directly located between the cavity of the proposed active site. This observation could result from protein stabilizing properties or resulting from the formation process of the cavity were residue ASP 159 and ARG 135 might play an important role.
References
[1] Shanon, C. E. (1948). A Mathematical Theory of Communication. The Bell System Technical Journal, 27, 379-423.
[2] Hamacher, K. (2008). Relating sequence evolution of HIV1-protease to its underlying molecular mechanics. Gene, 422(1-2), 30-36. doi:10.1016/j.gene.2008.06.007
[3] Weil, P., Hoffgaard, F., & Hamacher, K. (2009). Estimating sufficient statistics in co-evolutionary analysis by mutual information. Comput Biol Chem, 33(6), 440-444. doi:10.1016/j.compbiolchem.2009.10.003
[4] Altschul, S. F., Madden, T. L., Schäffer, A. A., Zhang, J., Zhang, Z., Miller, W., & Lipman, D. J. (1997). Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res, 25(17), 3389-3402.
[5] Sievers, F., Wilm, A., Dineen, D., Gibson, T. J., Karplus, K., Li, W., Lopez, R., et al. (2011). Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Molecular Systems Biology, 7(539), 539. Nature Publishing Group. doi:10.1038/msb.2011.75
[6] Hoffgaard, F., Weil, P., & Hamacher, K. (2010). BioPhysConnectoR: Connecting sequence information and biophysical models. BMC Bioinformatics, 11, 199. doi:10.1186/1471-2105-11-199.
 "
"