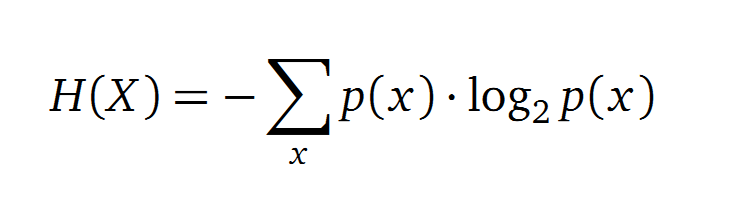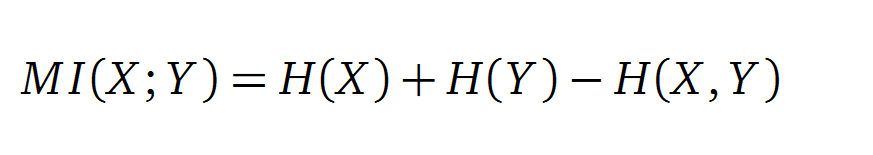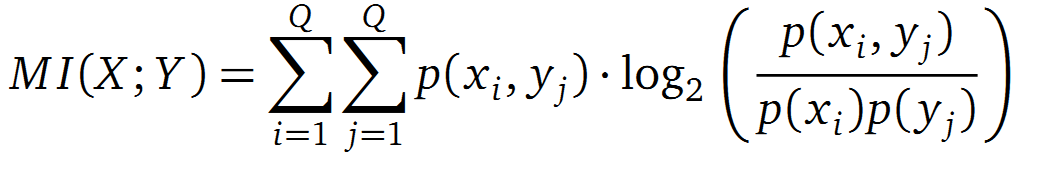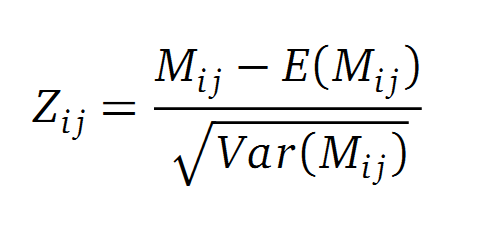Team:TU Darmstadt/Modeling IT
From 2012.igem.org
(→Fs. Cutinase) |
(→Fs. Cutinase) |
||
| Line 88: | Line 88: | ||
Here we show the entropy as a function of time. | Here we show the entropy as a function of time. | ||
[[File: mi.fsc.mat.png |700px|center]] | [[File: mi.fsc.mat.png |700px|center]] | ||
| - | Here we show the Z-score matrix as a heat map representation. | + | Here we show the Z-score matrix as a heat map representation. (Sicher die Zscores? sieht nach MI aus....) |
[[File: Sds.jpeg |700px|center]] | [[File: Sds.jpeg |700px|center]] | ||
Revision as of 17:59, 22 September 2012
| Homology Modeling | | Gaussian Networks | | Molecular Dynamics | | Information Theory | | Docking Simulation |
|---|
Contents |
Information Theoretical Analysis
Information Theory
Entropy
Claude Shannon created a measurement approach of uncertainty of a random variable X. This measurement is called Shannon entropy H [1] which is measured in bit, if a logarithm to the base 2 is used. p(x) denotes the probability mass function of a random variable X.
Mutual Information
In information theory, Mutual information (MI) measures the correlation of two random variables X and Y. H(X) and H(Y) are the Shannon entropies of the random variables X and Y. H(X,Y) is the joint entropy of X and Y. In other words, the MI quantifies the amount of information of variable X by knowing Y and vice versa.
Application of MI to sequence Alignments
It is well known that the MI can be used to measure co-evolution signals in multiple sequence alignments (MSA)[2] [3]. An MSA serves as a basis to investigate the functional or evolutionary homology of amino acid or nucleotide sequences. The MI of an MSA can be computed with the following equation in form of a Kullback-Leibler-Divergence (DKL):
with p(x) and p(y) being the probabilities of the occurence of symbols in column X and Y of the MSA. The joint probability p(x, y) describes the occurrence of one amino acid pair x i and y j and Q is the set of Symbols derived from the corresponding alphabet (DNA or Protein). The result of these calculations is a symmetric matrix M which includes all MI values for any two columns in an MSA. ?? A dependency of two columns acids shows high MI values. ??
Normalisation
A standard score (Z-score) indicates how many standard deviations a value differs from the mean of a normal distribution. MI dependent Z-scores can be calculated with a null model, where the symbols in MSA column are shuffled and every dependency of the column pairs are eliminated, but the entropy in each column is kept constant. The expectation value for the shuffle-null model is described by E(M ij) and its corresponding variance by Var(M ij) [4].
Method
Due to the the information theoretical analysis we are able to optimize our enzymes. To this end we have to create sequence alignments with a satisfying size. We obtained our sequences from the National Center of Biotechnological Information database (NCBI) using the Basic Local Alignment Search Tool (BLAST). We used an e-value cut-off of 105. To create an MSA we used the tool clustalo. The entropy and MI calculations were performed with R using the BioPhysConnectoR package.
Results
Fs. Cutinase
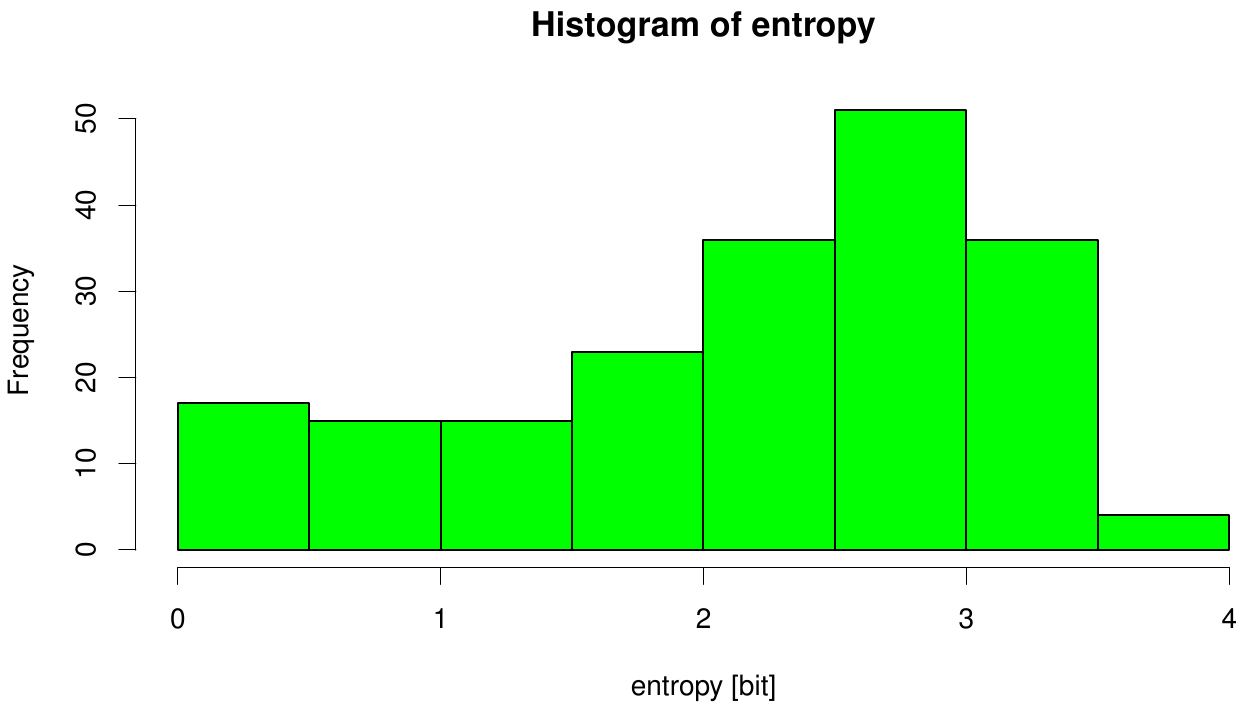
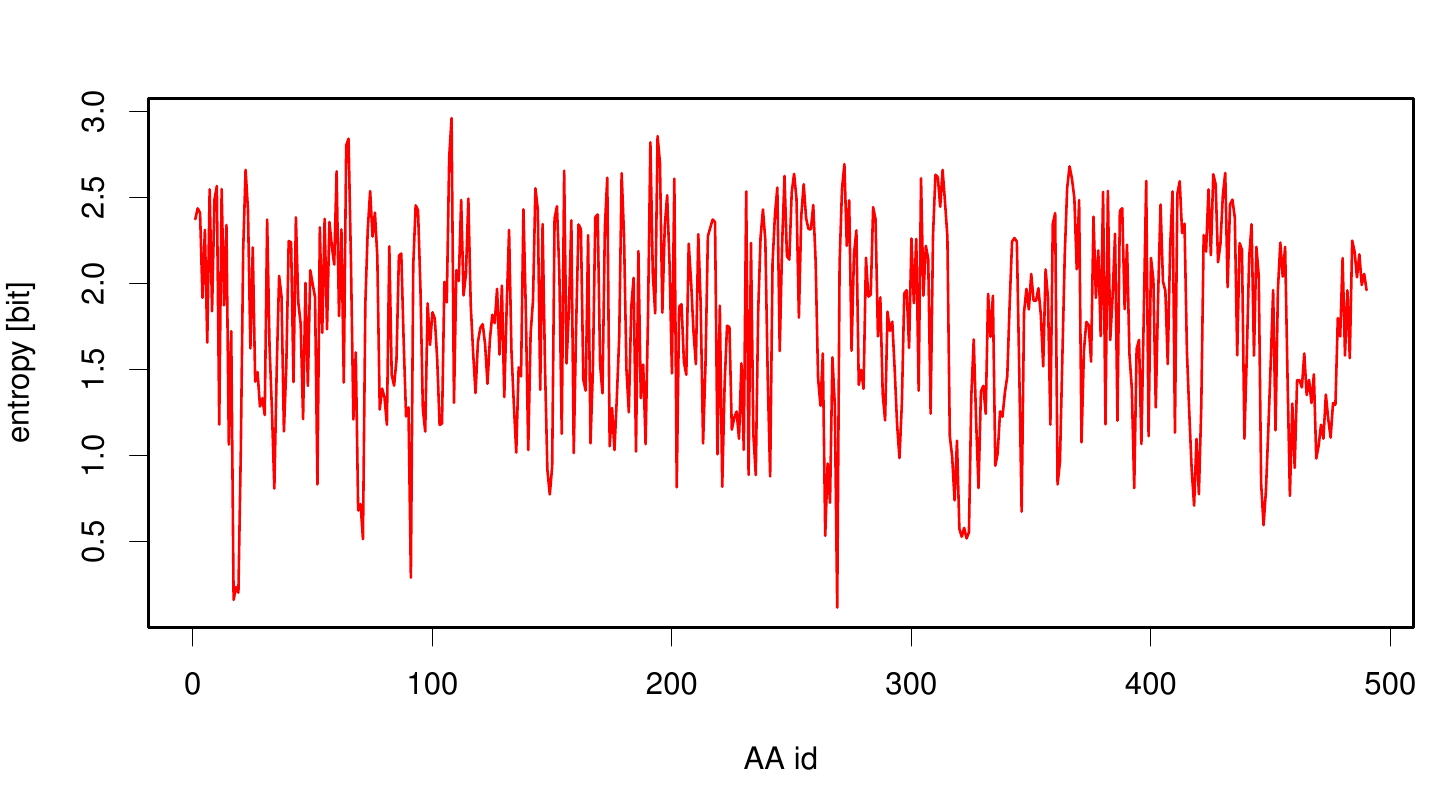
We utilized the entropy as a measure to detect evolutionary stable or conserved positions in sequence alignments. Moreover, these positions are considered to be essential for the stability or function of the protein.
Here we illustrate an histogram of entropy values derived from our Fs. Cutinase alignment. Notably the largest amount of entropy values is within a range from 2 to 3.
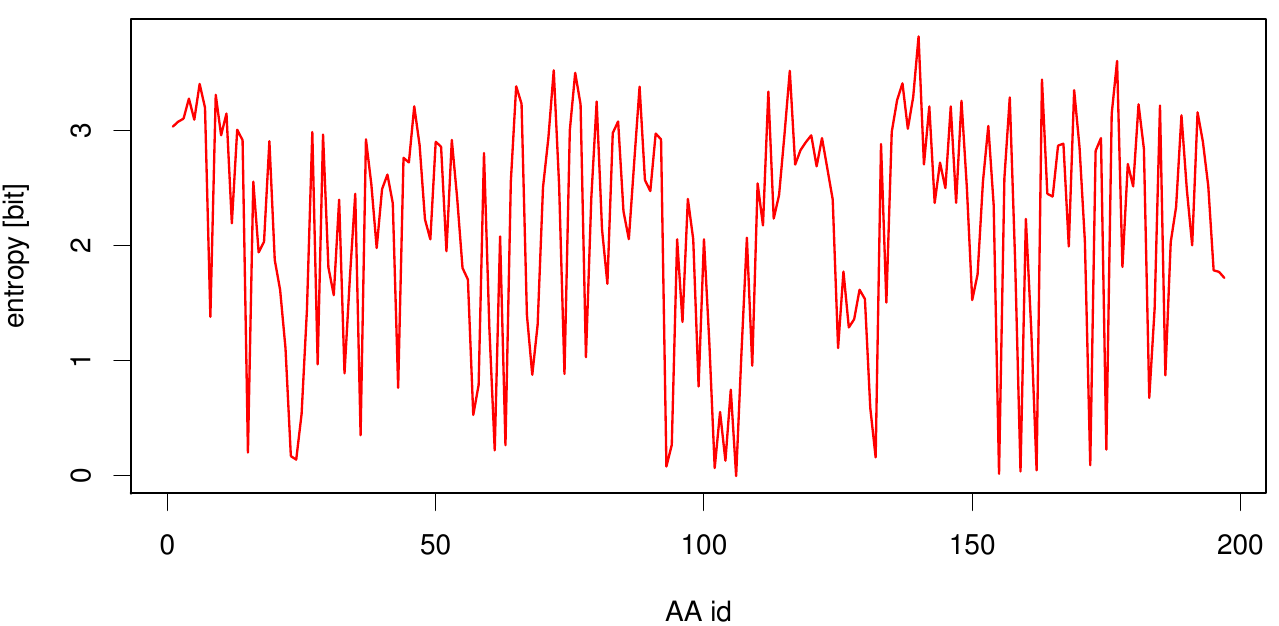
Here we show the entropy as a function of time.
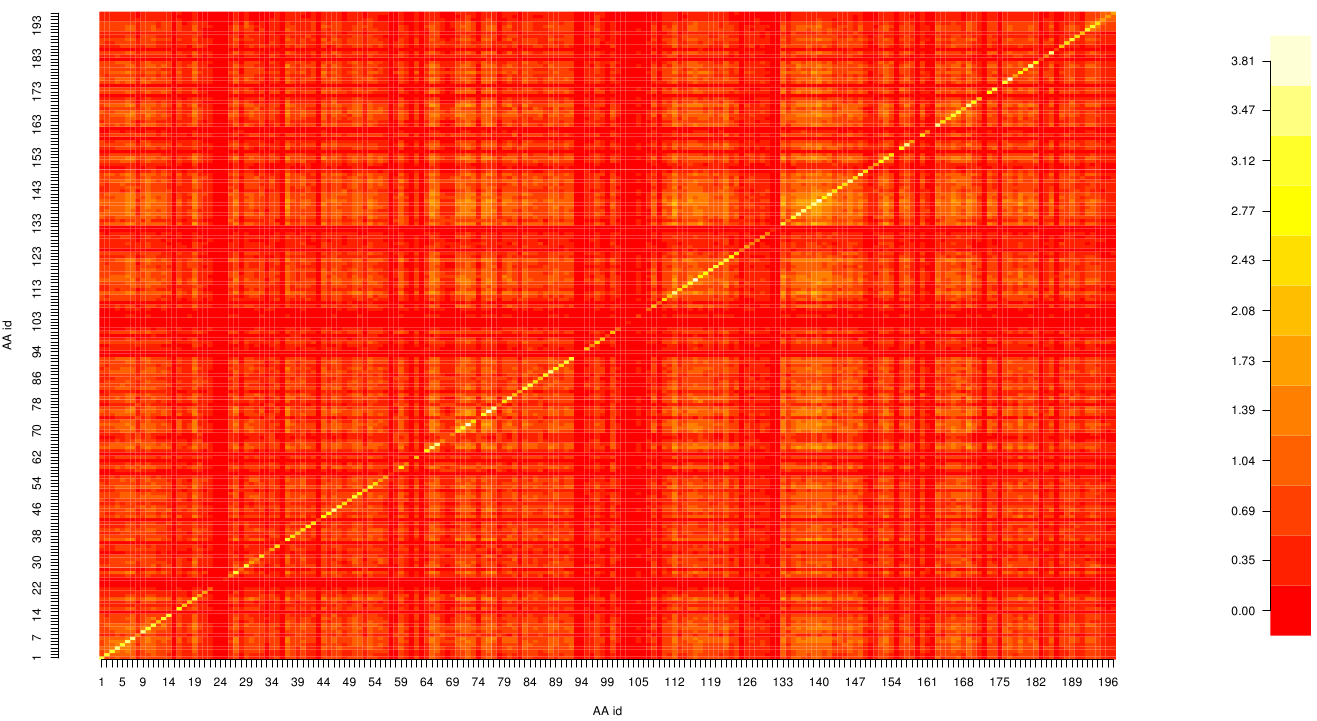
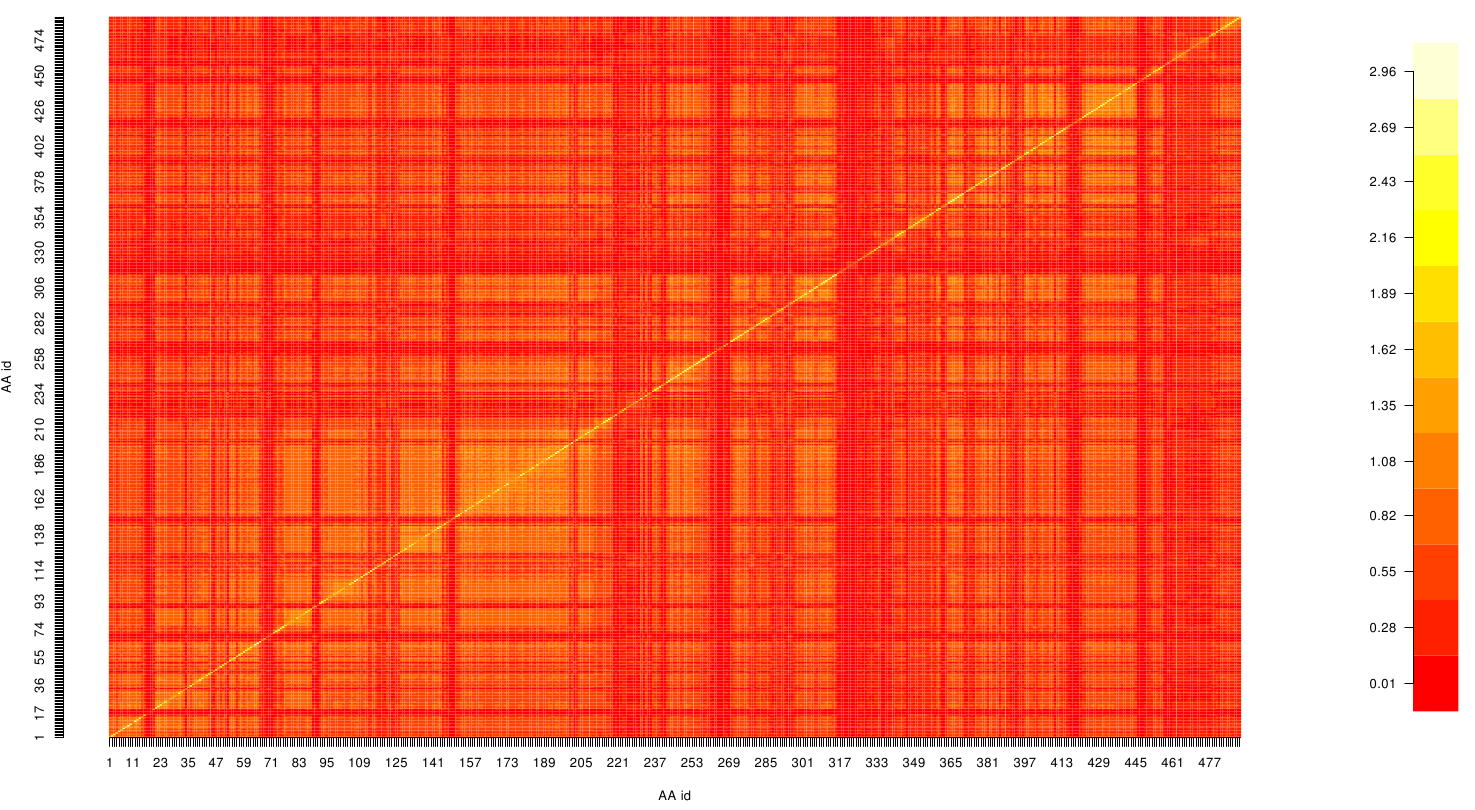
Here we show the Z-score matrix as a heat map representation. (Sicher die Zscores? sieht nach MI aus....)
 "
"