Team:Slovenia/ModelingDerivation
From 2012.igem.org
(Created page with "<html> <head> <meta http-equiv="X-UA-Compatible" content="IE=edge" /> <style type="text/css"> #container {background:#fff; margin:0 auto 0px; padding:5px 0px 0px; width:960px;...") |
|||
| Line 422: | Line 422: | ||
<img src="https://static.igem.org/mediawiki/2012/b/ba/Svn12_derivation1_eq4.png" /> | <img src="https://static.igem.org/mediawiki/2012/b/ba/Svn12_derivation1_eq4.png" /> | ||
</p> | </p> | ||
| + | |||
| + | <p>To account for non-linearity, an exponent n1 was added, and the equation generalized to: | ||
| + | <img src="https://static.igem.org/mediawiki/2012/a/a9/Svn12_derivation1_eq5.png" /> | ||
| + | </p> | ||
| + | |||
<p> | <p> | ||
Revision as of 22:05, 25 September 2012
Deterministic model derivation - genetic switch
The deterministic model for the mutual repressor switch was derived in the following way.
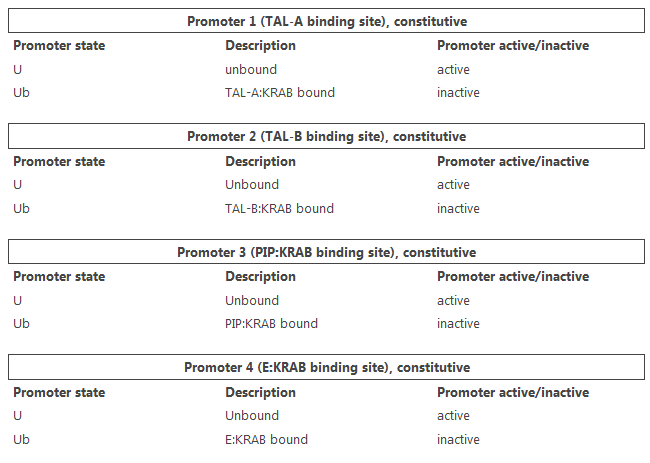
We assumed the following binding site states were possible:
Active promoter state is a state leading to gene expression.
Construct 1 promoter state transitioning is described by a reaction: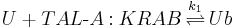
Assuming equilibrium of binding and unbinding, we can write:

The fractional occupancy of construct 1 promoter, f1, can be expressed as a ratio of active states to all states:

The equations for other constructs take the same form.
It follows that the fractional occupancy for construct 1 promoter is:

To account for non-linearity, an exponent n1 was added, and the equation generalized to:

Kr is the amount of TAL-A:KRAB it takes for f1 to be equal to 50%.
Derivation for constructs 2, 3 and 4 was similar except for different transcription factor names.
Fractional occupancies were then used to construct a set of ordinary differential equations representing each protein production. Because each protein can be produced from different constructs, production rates (including leaky rates) were summed together. E.g., because TAL-B:KRAB is produced from both constructs 1 and 3, fractional occupancies f1 and f3 were used and corresponding terms summed to obtain:

Since construct 5 promoter has no binding sites and is active at all times, fractional occupancy of the promoter is equal to 1.
The positive feedback loop switch model was derived in a similar manner.
 "
"