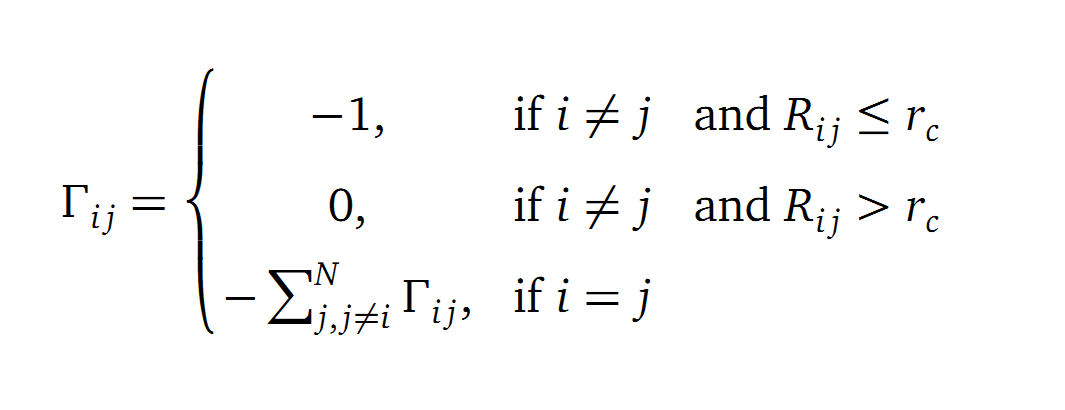Team:TU Darmstadt/Modeling GNM
From 2012.igem.org
(→Results) |
(→Results) |
||
| Line 76: | Line 76: | ||
* AroY | * AroY | ||
[[File: aroy_gnm.png |700px|center]] | [[File: aroy_gnm.png |700px|center]] | ||
| - | * | + | * TpHA3 |
[[File: TpHA1_gnm.png |700px|center]] | [[File: TpHA1_gnm.png |700px|center]] | ||
* TpHA2 | * TpHA2 | ||
[[File: TpHA2_gnm.png |700px|center]] | [[File: TpHA2_gnm.png |700px|center]] | ||
| - | * | + | * TpHB |
[[File: TpHA3_gnm.png |700px|center]] | [[File: TpHA3_gnm.png |700px|center]] | ||
* PnB-Esterase 13 | * PnB-Esterase 13 | ||
Revision as of 13:33, 20 September 2012
| Homology Modeling | | Gaussian Networks | | Molecular Dynamics | | Information Theory | | Docking Simulation |
|---|
Contents |
Gaussian network model
Theory
Nearly all biologically important processes such as enzyme catalysis, ligand binding and allosteric regulation occur on a large time-scale (micro- to millisecond). A Gaussian network model (GNM) is a coarse-grained representation of a protein as a network consisting of balls and springs. In our approach, the protein chain is reduced to the coordinates of the Cα atom of each residue, represented by a ball. The springs simulate the connection between the amino acids. While Molecular Dynamics (MD) simulations are computational expensive, a GNM calculation only needs a few seconds.
Computation
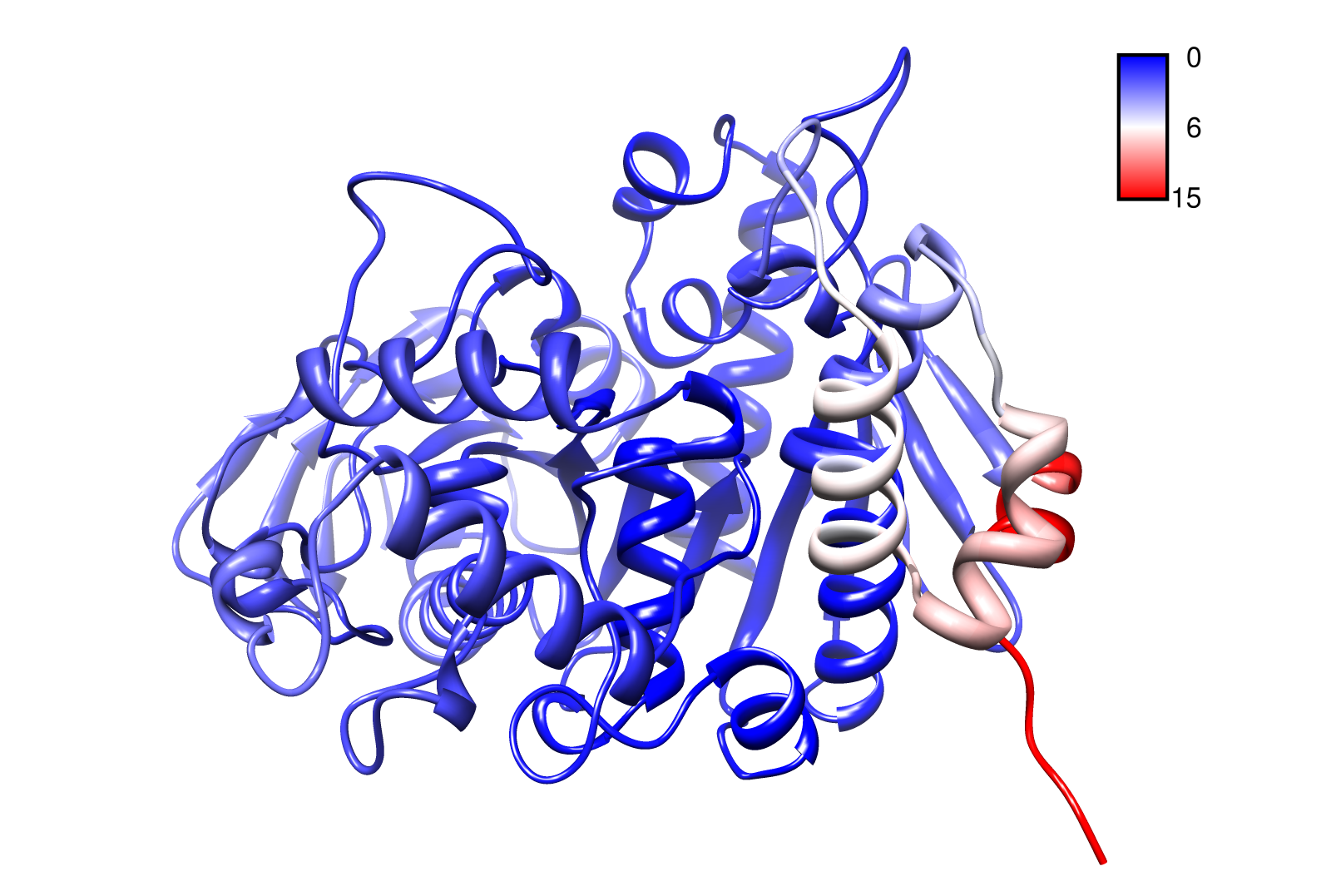
The dynamics of the structure in the GNM is described by the topology of contacts within the Kirchhoff matrix G. Thus in this network of N interacting sites, the elements of G are computed as:
where Rij is the distance between point i and j. We used Gamma as the intra Cα-contact matrix. The inverse of it describes correlations between fluctuations within the proteins native state. The diagonal of the matrix is replaced by the sum of contacts of one Cα-atom within the whole protein. After a singular value decomposition (SVD) we have calculated the normal modes of the protein. Slow modes describe functionally relevant residues within a biomolecule[2]. The opposite, Fast modes, represent an uncorrelated motion without significant changes in the structure.
A recent examination of the X-ray crystallographic B-factors of over 100 proteins showed that the GNM closely reproduces the experimental data [3].
Application to our Proteins
We computed the GNM in R [4] by using the BioPhysConnectoR [5] library.
- PnB-Esterase 13
- AroY
- TpHA1
- TpHA2
- TpHA3
Results
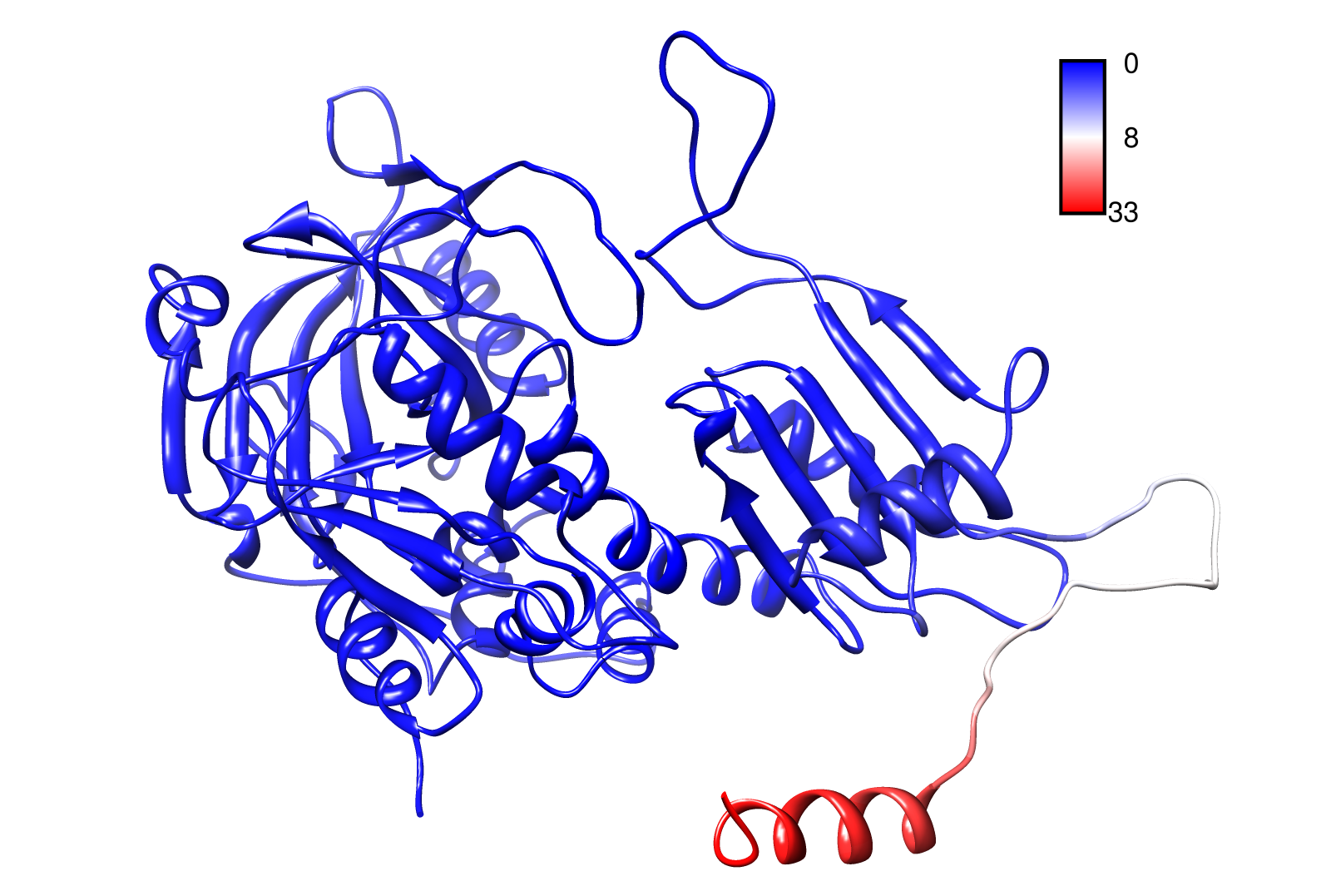
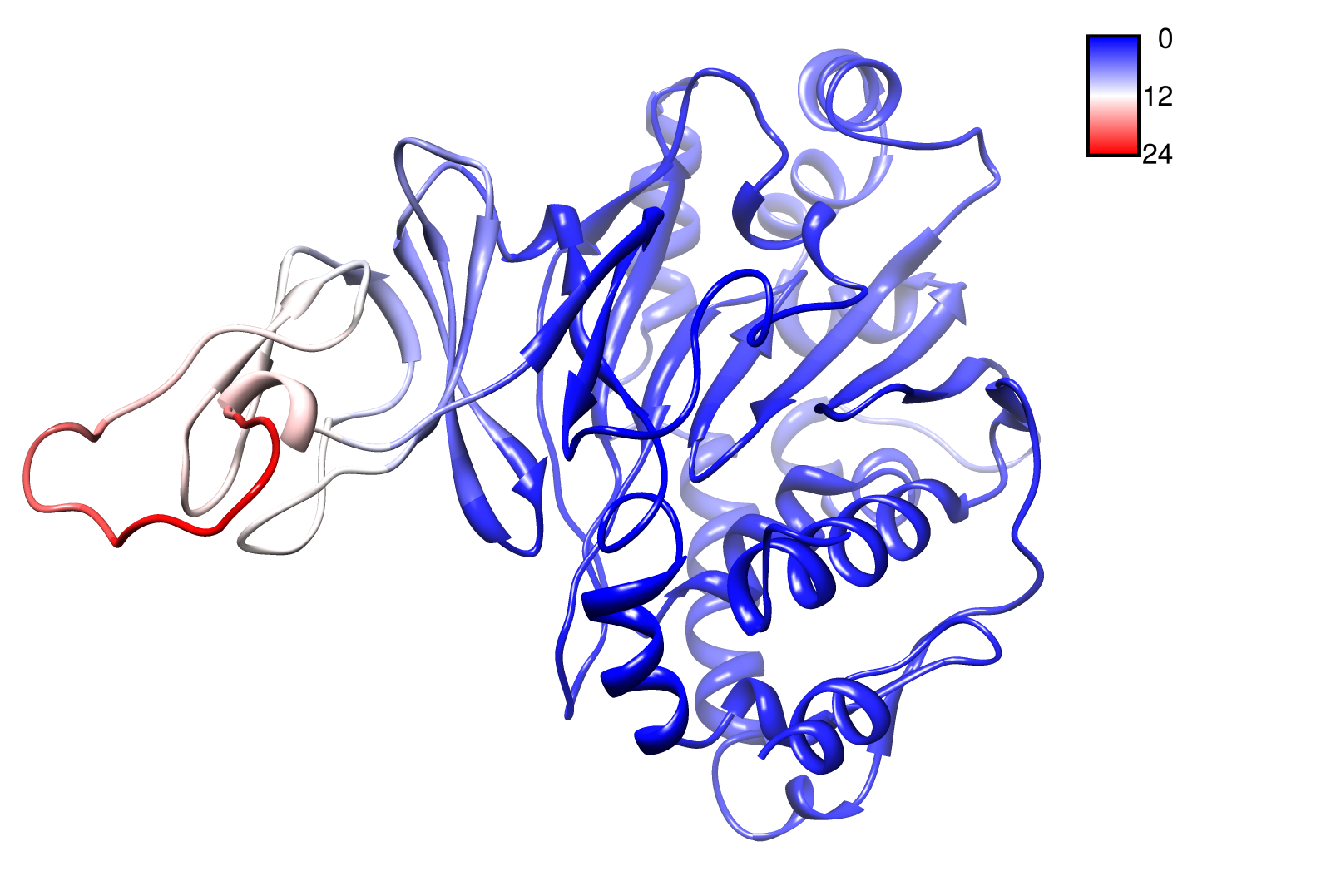
For the visualisation of the slow modes we colour coated the .pdb files. That actually means we replaced the atomic b-factors in our pdb files and substitute them with the slow mode values. Hence we are able to plot a heat-map on our protein structure.
- AroY
- TpHA3
- TpHA2
- TpHB
- PnB-Esterase 13
References
[1] A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar, “Anisotropy of fluctuation dynamics of proteins with an elastic network model.,” Biophys J, vol. 80, no. 1, pp. 505–515, Jan. 2001.
[2] C. Chennubhotla, A. J. Rader, L.-W. Yang, and I. Bahar, “Elastic network models for understanding biomolecular machinery: from enzymes to supramolecular assemblies.,” Physical Biology, vol. 2, no. 4, pp. S173–S180, 2005.
[3] I. Bahar and A. J. Rader, “Coarse-grained normal mode analysis in structural biology.,” Current Opinion in Structural Biology, vol. 15, no. 5, pp. 586–592, 2005.
[4] R. D. C. Team, “R: A Language and Environment for Statistical Computing.” Vienna, Austria, 2008.
[5] F. Hoffgaard, P. Weil, and K. Hamacher, “BioPhysConnectoR: Connecting sequence information and biophysical models.,” BMC Bioinformatics, vol. 11, p. 199, 2010.
 "
"