"
Team:Wageningen UR/Modeling
From 2012.igem.org
Contents |
Modelling
Formation of modified Virus-Like Particles is key to the success of our project. Therefore we first predict the structure of the subunits after which we use a model describing the formation of the whole VLPs.
In silico folding prediction
Introduction
We designed the construction of the subunits based on tertiary structure models. These models are generated by the web-based tool [http://www.sbg.bio.ic.ac.uk/phyre2/html/page.cgi?id=index Phyre2]. This server bases its prediction on both known structures and interactions between the amino acids. We used the tool to investigate whether the insertions and modifications cause any conformational changes to the subunits, which will most likely inhibit VLP formation.
Phyre2
We used Phyre2 to predict the tertiary 3D structure of both the wild type and the modified subunits. Phyre2 first compares the sequence of the input with a large database of over 10 million sequences. This creates an evolutionary comparison of the input data with known structures, which is placed in a Hidden Markov Model. After this first step, the same comparison is done with the whole database, but in an inverse way. Starting with the structure, the sequence in extracted after which a comparison is made with the same database, creating a new database of evolutionary fingerprints.
The Markov model of the input sequence is compared with this newly created database, creating a highly efficient comparison which only needs 15% homology to predict a new structure. A detailed explanation of this principle can be found [http://www.sbg.bio.ic.ac.uk/phyre2/html/page.cgi?id=help here].
Results
Hepatitis B outside modification
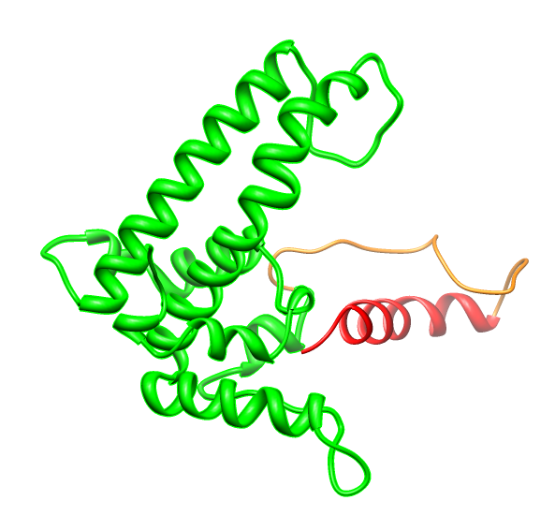
After making the prediction with Phyre2, the .pdb files were analyzed with the programs PDB viewer and Chimera 1.6.1 in order to create a visual alignment of the wild type and modified subunits. In case the alignment was, except for the insert, nearly complete, the construct was selected for further wetlab work. For the Hepatitis B core antigen it was already known that the outside loop would allow modifications. The rigidity of the coil however, could cause this structure to fall apart. Therefore, we assembled multiple amino acid sequences, all containing the same coil flanked by different linkers in order to maintain the structure and linearizing the coil. Figure 1 depicts the most simplistic of these investigations in which only the K-coil is added.
Hepatitis B inside modification
Looking at 3D models of the Hepatitis B VLP it can be seen that the C-terminal is presented on the inside. We also know that deletions to this part of the VLP can be done without influencing the assembly [1]. Since we want to package something inside the capsid it would be beneficial to delete as much of the C-terminal as possible - thus creating more space. Figure 2 shows the part we were able to delete from the wild-type core protein.
Comparing different possibilities to fuse the K-coil on the Hepatitis B core protein (with and without deletion of a part of the C-terminal, with or without a flexible linker, with or without a His tag) it was decided that the version with a C-terminal deletion and a flexible linker instead looks most promising (see figure 3 and 4).
Figure 2: Wildtype Hepatitis B - the part that can be deleted is marked black .
Figure 3: Hepatitis B with a flexible linker and a K-coil fused to the C-terminal .
Figure 4: Comparison Hepatitis B with inside modification [green - with red K-coil] - Hepatitis B wild type (with C-terminal deletion)[blue]. This shows that the folding of the main part is hardly influenced by the modification.
CCMV
Making a modification to the outside of CCMV however turned out to be more difficult in design. Literature does not give a clear indication of which part to modify in order to get the modification exposed to the outside of the VLP. We compared the structure of CCMV to that of HepB, in which we identified a loop on the outside of the VLP. Replacing part of this loop by adding a coil flanked by flexible linkers yielded the structure as compared in Figure 2. Although this idea seems promising, we did not continue because of indications in unpublished work from the Virology Department of Wageningen University. Besides, the coils seems to be in the area that interacts with neighbouring VLPs during assembly.
A second option for adding a modification to the outside of CCMV is modifying the N-terminus after adding a linker. This linker should give the coil the option to present itself at the outside of the VLP. Personal communication with Dr. richard Kormelink from the virology department did suggest that such a construct might leed to a coil on the outside of the VLP, as seen in Figure 3. Therefore we indicated this modification as the most promising in CCMV.
Figure 5: The wild-type CCMV (blue) is next to perfectly aligned with the modifyed CCMV (orange). The only two differences are the coil itself and the N-terminal part, which is not involved in VLP formation but in interaction with the RNA in the whole virus.
Figure 6: The K-coil that is attached to a linker (pink) clearly seems to tend to bend to a different location as the N-terminal part in the wild-type protein (blue).
Mathemathic VLPs assembly model
Introduction
In our project there are multiple aspects that we can model. Starting at the modelling of the formation of VLPs under different conditions, continuing at a dispersion model for when VLPs are injected into a human body and ending at marcro-models for degredation of VLPs in the environment. We chose to model VLP formation and aggregate formation.
VLP Formation
A VLP, which is a virus capsid without any genetic material, consists of a certain number of subunits or monomers. These subunits are viral proteins, which for our project are made to be expressed by E.coli and then made to re-assemble in vitro.
For modelling our VLPs we needed to find a model which could fit the assembly of our entire virus like particles, namely, CCMV, HBV and Polerovirus.In the case of CCMV, there are 180 subunits which go on to form capsomeres in the form of pentamers or hexamers and self-assemble according to the triangulation number, T=7 to form a capsid approximately 28nm in diameter. The CCMV capsid consists of 12 pentameric capsomeres and 20 hexagonal ones [2]. But for the sake of modelling, we take an average of it forming 36 pentameric capsomeres.
Presently, assembly of virus particles is not fully understood and different idealized models and theories are present which try to explain the assembly process. One such theory is the classical nucleation theory. In this the first step is the self-association reaction which begins with a nucleation event (the formation of a dimer). This dimer then serves as the basis for elongation through sequential addition of free subunits, one at a time, to nuclei to form partially assembled intermediates which results in a closed icosahedral VLP as shown in figure 7. Nucleus formation is regarded as the rate-limiting step [3].
We chose this model because it competitively accounts for the partitioning of the protein subunits between correct and the aggregation pathways. Using this, we can estimate losses through aggregate formation and also estimate the yield of the VLPs once the parameters have been determined.
The critical concentration of capsomeres is the concentration below which no VLP formation will take place. Therefore, to be able to form VLP's, the total concentration of capsomeres should be higher than the critical concentration. To establish this, we assume the concentration of capsomeres available for VLP formation (C) to be equal to the total concentration (Ctotal) minus the critical concentration (Ccritical)[3]:
(1) C = Ctotal – Ccritical
It is considered that a dimer is the first species (nucleus) formed in the reaction, and is subsequently consumed to form higher-order intermediates by the addition of free subunits (capsomeres). Two capsomeres will go on to form a dimer (rate limiting step), whose concentration is defined by C2. The rate of change of concentration of dimers with time, depends on kv,critical (M-1 s-1) which is the nucleation rate constant and kv (M-1 s-1) the elongation rate constant, given by the equation [3]:
(2) dC2/dt = (1/2) * kv,critical * C^2 – kv * C * C2
The aggregation of the viral protein is modelled by a second-order reaction describing the agglomeration of two capsomeres, where A is the aggregate concentration and kA (M-1 s-1) the aggregation rate constant[3].
(3) dA/dt = (1/2) * kA * C^2
The capsomere concentration will continuously drop, depending on the rate of dimer formation, elongation and aggregate formation. This equation is given by [3]:
(4) dC/dt = kV,critical * C^2 - kV * C * ∑_(i=2)^(s-1)[Ci] - kA * C^2
On the path to the formation of the VLP, due to elongation intermediates are formed, with the first one (3 capsomeres long) forming after the elongation of a dimer. The equation for the formation of intermediates, with i being the number of subunits in a given intermediate, is given by [3]:
(5) dCi/dt = kV *C * (Ci-1 - Ci); i= 3; 4; . . . ; s-1
The last step of the process is the formation of the VLP. The VLP concentration is the end result of the elongation to the biggest possible intermediate (s-1), s being the number of subunits in a correctly formed VLP[3]:
(6) dV/dt = kV * C * Cs-1
where V is the VLP concentration, s is the number of subunits in a correctly formed VLP (36 in the case of CCMV), and i is the number of subunits in a given intermediate. The initial conditions at t=0 were set as C=C0 and C2 = C3 =...... = C35= V=A=0.
The initial conditions at t=0 are C=C0 and C2 = C3 =...... = C35= V=A=0.
For our model, we ran simulations using MATLAB 2012. Values for the parameters, Ccritical = 0.02 mg/ml, kV,critical =2 ,kV = 1000 and kA = 10 were assumed. It should be noted that, since the rate constants would be in M-1 s-1 and the concentration in mg/ml, an intermediate Ci would weigh i times the weight of a capsomere. So, in the end, the VLP would weigh s times the weight of a capsomere. This was introduced into our model script and the resulting simulation (Figure 8) was obtained.
Figure 8: Simulated graph showing concentration profiles of the different components with time
Our model predicts that for the assumed set of parameters, almost 75% of the capsomeres form VLPs and the rest go on to form aggregates after 8 hours.
Since the model depends on the total number of subunits in a VLP and certain parameters, it can be applied to the self-assembly of any virus-like particle composed of one kind of viral protein. The parameters can then be determined by incorporating experimental data measuring the concentration profiles of the proteins involved under differing conditions and analyzing the components put through the required purification steps. All this information can be combined with the model in MATLAB to give true values for the parameters. Due to a combination of time constraints and unavailability of instruments like asymmetrical flow-field flow fractionator, bioanalyzer etc to purify and measure concentrations of capsomere, VLPs and aggregates effectively we could not achieve this.
Self-assembly of VLPs occurs at certain conditions (pH, salt concentration, temperature). This self-assembly then is dependent on the rate constants (kV,critical,kV and kA) involved in the dynamics. In theory, the elongation rate constant kV should be much larger than kV,critical and kA. This would drive the system towards formation of VLPs. Also, ideally the kA should be smaller than the kV,critical which would mean, dimer formation is more dominant than aggregation, but this is rarely the case. So, ultimately, if one has the required instruments at their beck and call, the parameters could easily be determined and VLP production could be maximized and losses through aggregation, minimized.
References
1. Beterams, G., Böttcher B., & Nassal M. (15. Sept 2000). Packaging of up to 240 subunits of a 17 kDa nuclease into the interior of recombinant hepatitis B virus capsids. FEBS Lett., S. 169-76.
2.Johnson, J. E. and J. A. Speir (1997). "Quasi-equivalent viruses: a paradigm for protein assemblies." J Mol Biol 269(5): 665-675.
3.Ding, Y., Y. P. Chuan, et al. (2010). "Modeling the competition between aggregation and self-assembly during virus-like particle processing." Biotechnol Bioeng 107(3): 550-560.
