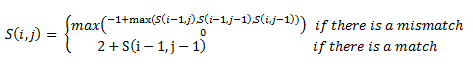Team:BYUProvo/Modeling
From 2012.igem.org

|

|

|
| Home | Team | Team Profile | Project | Parts | Modeling |
|
Safety | Outreach | Collaboration | Attributions |
Contents |
Introduction
Colon cancer polyps produce high amounts of reactive oxygen species (ROS) and lactate. The high metabolic activity also causes an increase in temperature. Sensors for any one of these inputs alone would be confounded by normal physiological variation in temperature, lactate concentration, and ROS concentration. We propose a genetic circuit designed to detect higher than normal levels of all three, producing two separate outputs. There are two parts to the circuit: The first is a dual input system, using temperature and ROS as inputs to produce an output (LacZ). The second is a single input system, using lactate to produce GFP.
Insert picture of model here
In order to model our system, we have undertaken three main tasks:
1) Create a model using Mass-Action Enzyme Kinematics
2) Analyze this model using computational methods
3) Create an algorithm to predict the structure of our RNA thermosensors
We will start by describing the reactions within our circuit and then by creating a system of differential equations from the reaction sequence.
Our Circuit
Insert picture of circuit here.
The diagram above depicts the inner workings of our circuit created within E. Coli. The following chemical equations depict the pathway:
Insert chemical equations here.
The Model
Mass-Action Equations
Using mass-action kinetics, we write these chemical equations as a system of differential equations.
Insert ODEs here
System of ODEs
As it is, the system is too complicated for us to analyze, so we hereby make a few assumptions to simplify.
- Quasi Steady-State Assumption
- Forward Reaction Assumption
Temperature Dependence
Parameter Estimation
Experimental Data from Lab Work
Analysis
Bifurcation Analysis
Steady State Analysis
Modeling our Thermosensor
Herein we provide detailed information about our library of thermosensors and describe our attempt to model the secondary structure of the RNA hairpins.
Smith-Waterman Algorithm
The Smith-Waterman Algorithm is a simple process used to perform sequence alignment. To demonstrate how the algorithm works, we will use these two sequences:
- ACUAGGUA
- AGCUAGGA
First one sequence is placed in the first row of a grid, skipping the first two entries in the row. The second is likewise placed in the first column, skipping the first two entries in the column. Zeros are then placed in row 2 and column 2.
SM#1
Then, a scoring matrix, S is created according to the following rules:
For example S(4,8) in the blue was obtained by adding 2 to the number in the entry in the upper left-hand corner. S(7,7) was obtained by adding -1 to the max of the 3 numbers above, on the upper left-hand corner, and to the left of it.
SM#2
Once the scoring matrix has been completed, starting in the bottom right corner, a path is chosen, picking the largest numbers (only numbers to the left, above or up and to the left can be chosen), until the path arrives back at a zero. When a number above or to the left is the same as the number on the diagonal, the number above or to the left is to be chosen first.
SM#3
The resulting path spells out the proper alignment of the two sequences. Squares alone in their row and column represent an alignment and when two or more squares share the same column or row, the one closest to the bottom right corner is the one that represents the alignment. The other squares represent deletions or insertions. Therefore, for our example, the final alignment would be:
SM#4
Thus the alignment of the two sequences would be:
- A--CUAGGUA
- AGCUAGG--A
 "
"