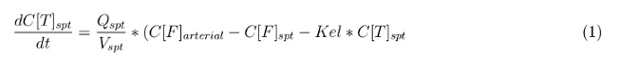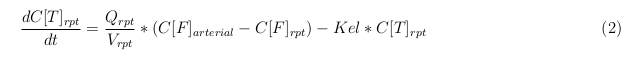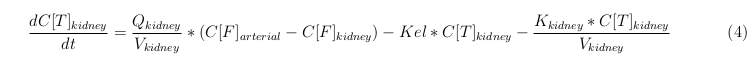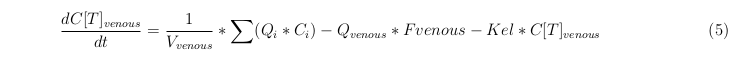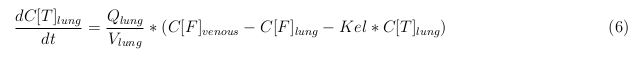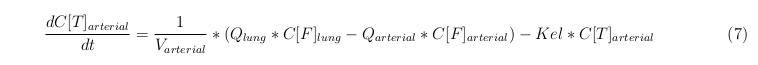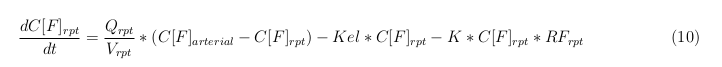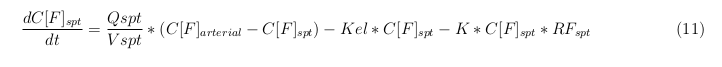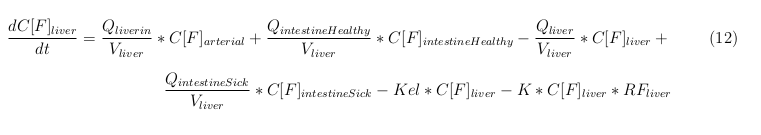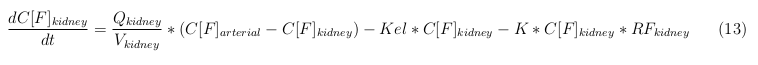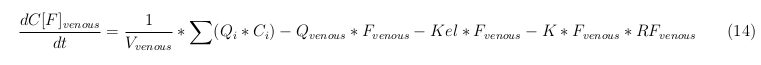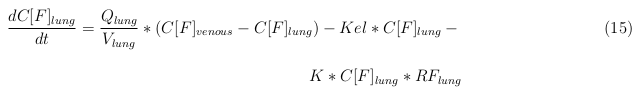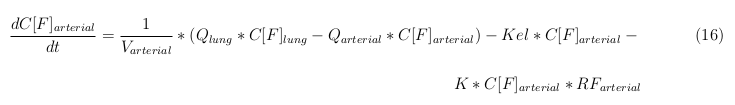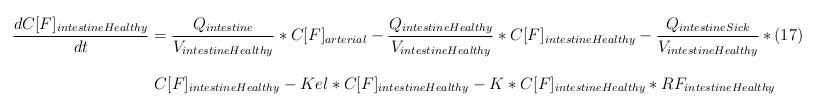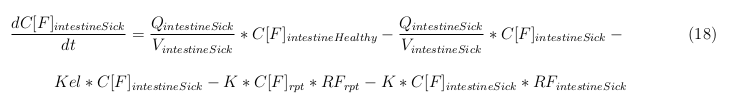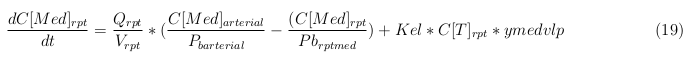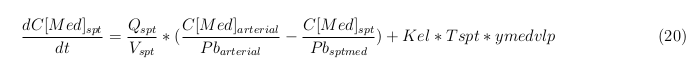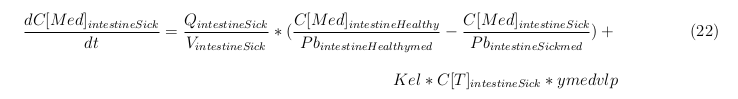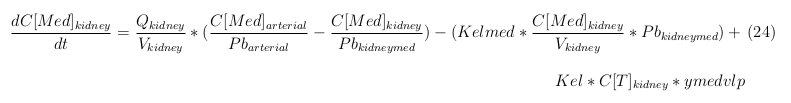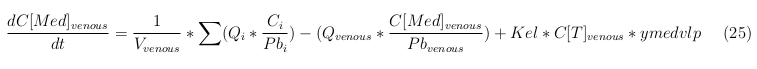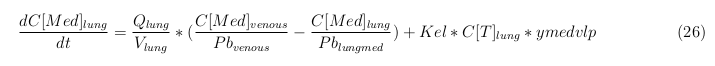Team:Wageningen UR/HumanBody
From 2012.igem.org
MarkvanVeen (Talk | contribs) (→Explanation of the model) |
MarkvanVeen (Talk | contribs) (→Results) |
||
| Line 176: | Line 176: | ||
== Results == | == Results == | ||
| - | |||
| - | |||
| - | |||
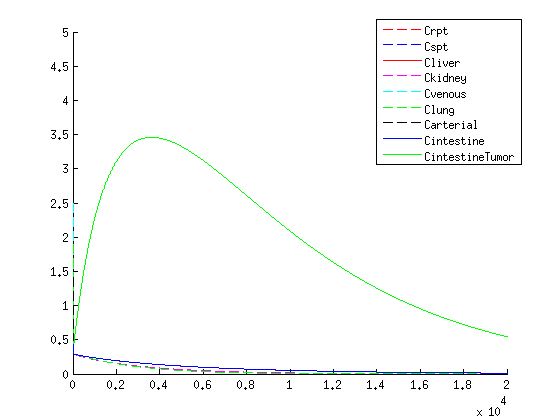
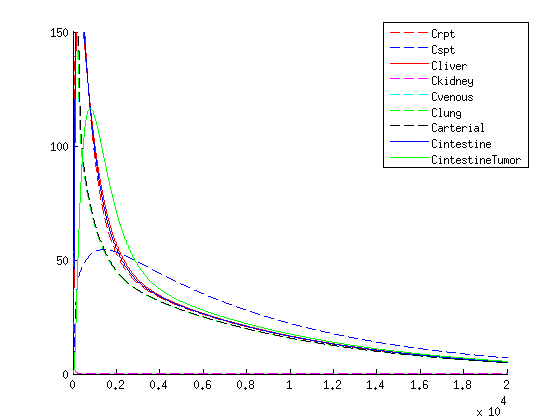
| - | + | [[File:VLPconcWITHMED.png|thumb|"Concentration over time of VLP within the human body according to the model"]] | |
| - | + | ||
| - | + | ||
| - | + | ||
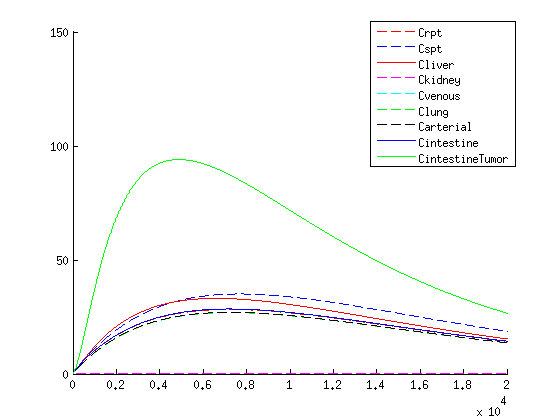
| - | + | [[File:VLPWITHMEDconc.png|thumb|"Concentration over time of medicine within the human body according to the model"]] | |
| - | [[File:MEDconc.png]] | + | |
| + | |||
| + | [[File:MEDconc.png|thumb|"Concentration over time of the medicine when not packaged within a VLP"]] | ||
== Discussion/Conclusion == | == Discussion/Conclusion == | ||
Revision as of 13:58, 26 October 2012
Contents |
Human Body Model
To be able to determain what the vlps and the medicine do in the human body we've constructed a human body model that is inspired by the model of the Slovenia 2012 team. With this model we are able to compare the traditional use of medicine with the use of our VLPs. If succesful it will open up a whole new era for the use of medicine.
Explanation of the model
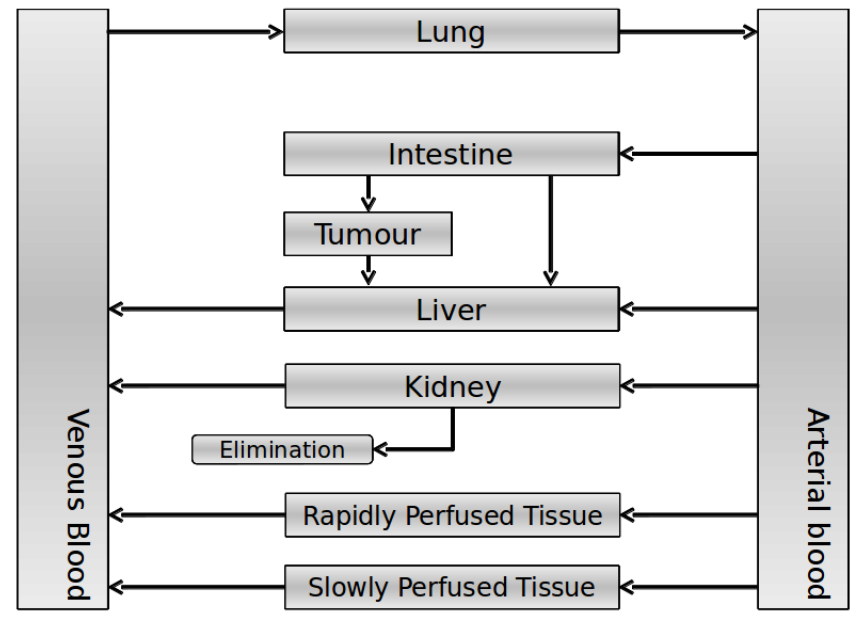
Our model is constructed in such a way that each compartment of the model represent an organ or multiple organs with the same physical properties. We decided to have separate compartments for the kidneys, liver, lungs and the intestine. All other organs are grouped in the rapid or slowly perfused tissue. In the case study we made a new compartment between the intestine and the liver to represents the intestine tumor (figure 1).
In our model we’ve used three different mass balance equations for an organ. The first mass balance describes the concentration of all the VLPs in the organ, this is to see the overall change in the VLP concentration. The second mass balance equation describes the concentration of the unbound VLPs. This is because the unbound particles can move freely into the body while the bound particles stays into the organ. The final mass balance equation is for the concentration of the medicine in the organ. With these three mass balance equation we’ve developed our model.
General mass balance equations for all the VLPs
The equations below describe the change in concentration of all the VLPs in the different organs. The mass balances for the different organs consists out of multiple parts. Each organ as at least an flow that describes the concentration of VLPs that come into the organs and a flow that describes the VLP concentration that goes out of the organ. Also each organ has a rate of decay incorporated into the mass balance to describe the falling apart of the VLPs in the different organs. The mass balance of the kidney has also an equation for the removal of the VLPs via the urinal track.
Slowly perfused tissue
Rapid perfused tissue
Liver
Kidney
Venous
Lung
Arterial
Intestine Healthy
Intestine Sick (Tumor)
General mass balance equations for the unbound VLPs
Besides needing an equation to describe the change in concentration of all the VLPs, we also need an equation to describe the change in concentration of the unbound VLPs for each organ. The mass balances for the different organs consists out of multiple parts. The mass balances are similar to the mass balance for all the VLPs, with a slight difference, it’s has a rate of VLP attachment. This rate describes the attachment of the VLPs onto the surface of the cell.
Rapid perfused tissue
Slowly perfused tissue
Liver
Kidney
Venous
Lung
Arterial
Intestine Healthy
Intestine Sick (Tumor)
General mass balance equations for the medicine
The last set of mass balances are for the change of concentration of the medicine in the different organs. These equations consists out of multiple parts, similar to the previous set of mass balances. Each organ as at least an flow that describes the concentration of medicine that come into the organs and a flow that describes the medicine concentration that goes out of the organ. Also each organ has a rate of decay incorporated into the mass balance to describe the decay of medicine in the different organs. The mass balance of the kidney has also an equation for the removal of the medicine via the urinal track.
Rapid perfused tissue
Slowly perfused tissue
Intestine Healthy
Intestine Sick (Tumor)
Liver
Kidney
Venous
Lung
Arterial
Case study: colorectal cancer
As our case study to use the human body model, we used colorectal cancer. Cancer as a disease is very destructive and is responsible for the deaths of millions. In 2007, 13% of all the deaths were cancer related [1]. We chose colorectal cancer because in Europe the 5 year survival the disease is less than 60% [2]. If our treatment shows a better treatment we can help the people to fight off the cancer.
Treatment of Colorectal cancer
The conventional way to treat colorectal cancer includes surgery and chemotherapy if the cancer is detected in an early stage, when it detected in a later stage treatment is often directed more at extending life and keeping people comfortable [2]. The agents used for chemotherapy are fluorouracil, capecitabine, UFT, leucovorin, irinotecan, or oxaliplatin. Side effects [3] of the agents are:
- Acute central nervous system damage
- Bone marrow suppression
- Mucositis, inflammation of the mucus membranes of the GI track
- Dermatitis, inflammation of the skin
- Diarrhoea
- Nausea
- and many more
We believe, if we can focus the agent around the tumor we’ll able to reduce the side effect and create a better chemotherapy treatment for cancer patients.
Parameters
For the distribution of VLPs throughout the human body, used parameters were obtained from the documentation Slovenia 2012 or from literature sources [4]. The estimated parameters for the organs in table XXX are explained as followed: Blood-flow, the amount of blood in liters flushing throughout the organs, Volumes, the size of the organ, Receptor, the concentration of receptors in µM and the partition coefficient of the medicine that is packaged within the VLP.
| Organ | Blood-flow [L/min] | Volume [L] | Receptor 1 [uM] | Partition coefficient medicine |
| Slowly perfused tissue | 2.12 | 53.2 | 0.237 | 100 |
| Rapidly perfused tissue | 1 | 3.61 | 0.237 | 100 |
| Kidney | 1.06 | 0.31 | 0.237 | 100 |
| Liver | 1.4 | 1.82 | 0.237 | 100 |
| Lung | 5.58 | 0.56 | 0.237 | 100 |
| Intestine Healthy | 0.94 | 4.41 | 0.237 | 100 |
| Tumor | 0.1 | 0.49 | 10.716 | 100 |
| Arterial | 5.58 | 1.7 | 0.237 | 100 |
| Venous | 5.58 | 3.9 | 237 | 100 |
Parameters that were estimated for non organ variables are found in table 2 and are explained as followed. Affinity constant for receptor, is the binding affinity of the VLPs to the receptor on the cell surface. VLP elimination rate is the half-life of the VLPs. VLP Renal removal rate is the removal rate of the VLPs within the kidneys [5]. Medicine elimination rate is the removal/degradation of the medicine within the human body [6]. The last parameter is the packaging constant which encapsulate the amount of medicine in µmol within a single VLP.
| Affinity constant for receptor | 0.001 |
| VLP elimination rate | 0.000143 |
| VLP Renal removal rate | 0.000403 |
| Medicine elimination rate | 0.05 |
| Packaging constant | 300 |
Results
Discussion/Conclusion
Mark/Jasper
Remarks
With this model it becomes possible to simulate the VLP and medicine distribution in the human body. However this model, like every model, has it's limitations. Though there are several limitations in the model, it can be used for different scenarios involving the use of VLPs. In this paragraph we'll discus the limitations and it's possibilities of this model and how we can improve this model.
Important parameters
One of the major limitations of every model is the lack of information to determine the parameters. This is the same in this model, shown below is a list of the parameters we've estimated by the little information we've had. If better information becomes available we'll be able to predict a more precise simulation on how the medicine distribute around the body.
- Ratio of receptor concentration between tumor and healthy tissue
- Stability of the VLP
- Packaging quantity of the VLP
- Binding affinity of the VLP to the receptor
- Medicine absorption of tumor / healthy cells
- Distribution of receptors on cell surface
Future work
To improve this model several things can be done. First of all, research should be done on several parameters of the model. Specially parameters involving the number of receptors and the breaking down of VLPs. Second looking into other models to further improve the mass balance equations to get a more accurate and faster result. Besides looking for things to build upon, we also want to look at the limitations the model has and how to remove those limitations, creating a more solid model.
References
- Jemal A, Bray, F, Center, MM, Ferlay, J, Ward, E, Forman, D; "Global cancer statistics", 2011, CA: a cancer journal for clinicians 61 (2): 69–90
- Cunningham D, Atkin W, Lenz HJ, Lynch HT, Minsky B, Nordlinger B, Starling N; "Colorectal cancer.", 2010, Lancet 375 (9719): 1030–47
- Dr. Mark D. Noble, Chemotherapy-induced Damage to the CNS as a Precursor Cell Disease, University of Rochester
- Benjamin L. Shneider; Sherman, Philip M, Pediatric Gastrointestinal Disease, 2008,Connecticut: PMPH-USA. pp. 751.
- Kaiser CR, et al., Biodistribution studies of protein cage nanoparticles demonstrate broad tissue distribution and rapid clearance in vivo, 2007, Int J Nanomedicine, 2(4):715-33.
- Longley DB, Harkin DP, Johnston PG, 5-fluorouracil: mechanisms of action and clinical strategies", 2007, Nat. Rev. Cancer 3 (5): 330–8
 "
"