Team:Peking/Modeling/Ring/Simulation

From 2012.igem.org

(Difference between revisions)

Revision as of 05:07, 26 October 2012

Home
Team
Project
Data Page
Modeling
Human Practice
Safety

- Data Page
- Judging Criteria

ODE Model

According to the previous circuit and ODE model, we listed all the differential equations and simulated this system in MATLAB with equations listed as below:

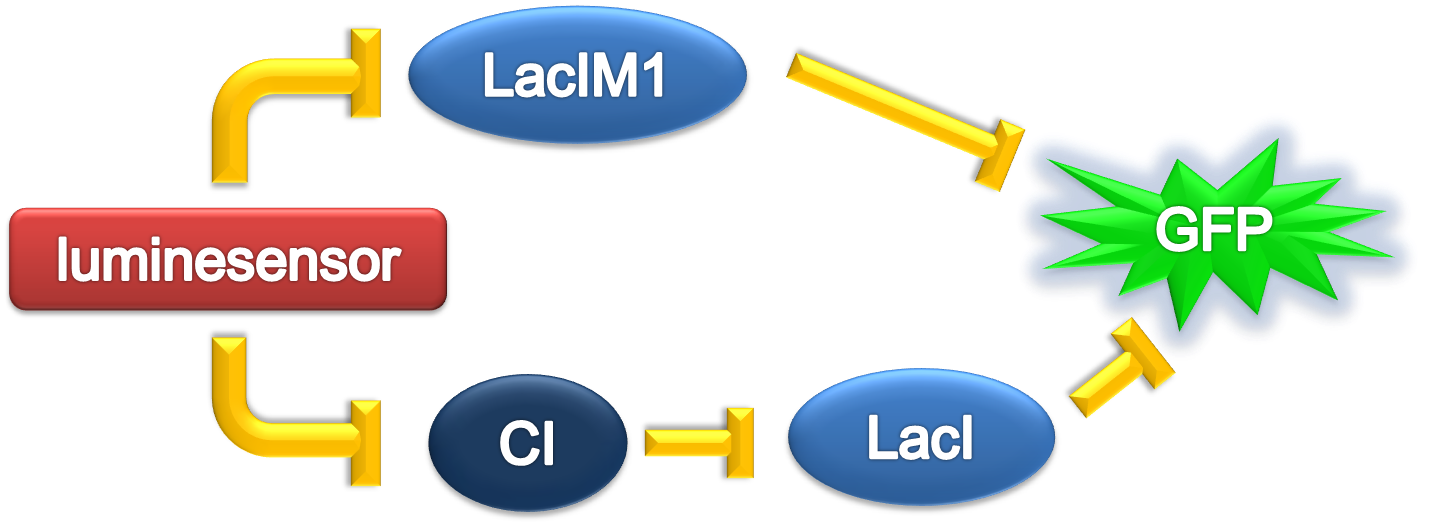
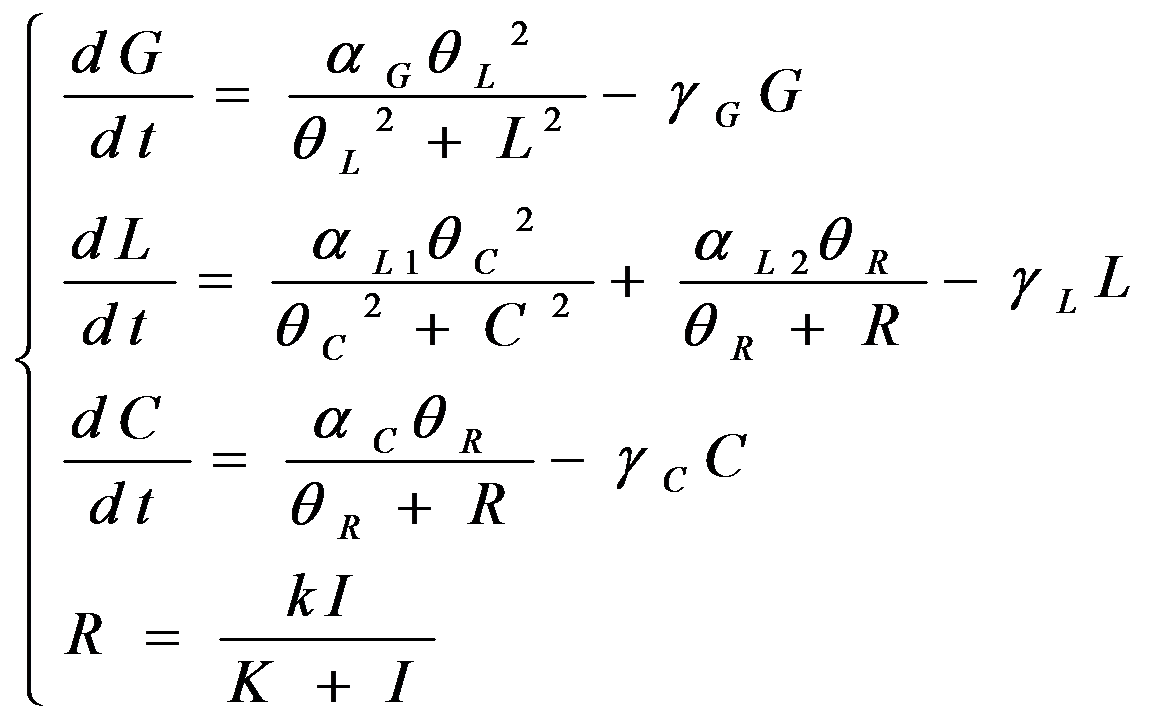
We applied the inverse square law to describe the light intensity distribution on the plate according to different radius, with a central intensity I₀ in a region of r=1mm. Here, parameters are:

Parameter	Value	Unit	Description	Source
a_G	2	10^-6M/min	GFP production rate constant	[1]
a_C	2	10^-6M/min	CI production rate constant	[1]
a_L1	1	10^-6M/min	LacI production rate constant	[1]
a_L2	1	10^-6M/min	LacIM1 production rate constant	[1]
b_C	8.x10^-3	10^-6M	Binding strength of CI on LacI operator	[1]
b_L	8.x10^-1	10^-6M	Binding strength of LacI or LacIM1 on GFP operator	[1]
b_R	1.x10^-2	10^-6M	Binding strength of Luminesensor on corresponding operator
r_G	6.92x10^-2	min^-1	GFP dissociation rate constant	[1]
r_C	6.92x10^-2	min^-1	CI dissociation rate constant	[1]
r_L	2.31x10^-2	min^-1	LacI and LacIM1 dissociation rate constant	[1]
I₀	1000	AU	Maximum light intensity in the middle of the plate
k	500	10^-6M	Luminesensor activation rate under light
K	10000	AU	Light sensitivity of Luminesensor activation

The simulation results in static state are shown below:

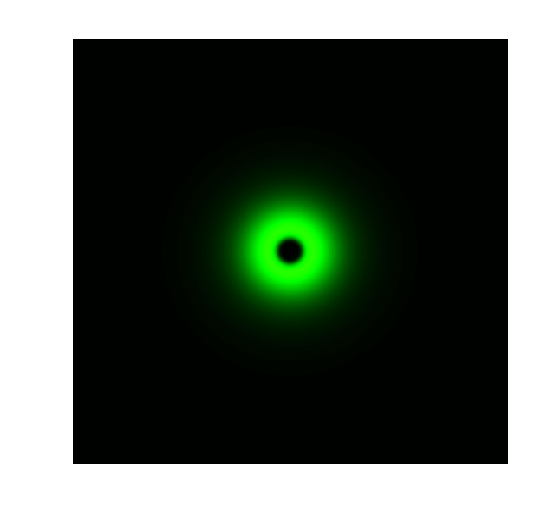
Figure 1. ODE Simulation in a plate of the ring-like pattern formation.

Figure 2. ODE Simulation for the radial expression amplitude of the ring-like pattern formation.

From the Figure 1 & 2 above, we discover that, with wildtype parameters, ring-like pattern is formed based on sender-receiver communication through bio-luminescence.

Parameter Analysis

After modeling the ring-like pattern formation with wildtype parameters, we attempted to optimize it in a rational way. We have tuned the parameters both up and down, one by one, and finally discovered several parameters which predominantly influence the expression intensity, ring radius, and band width of pattern formation.

Parameter	Function	Description	Remark
a_G/r_G	If increasing, the expression intensity will be amplified, but the ring radius and the band width will not change.	Related to the production and dissociation of GFP	The production rate of GFP is easily tuned.
a_C/(b_C*r_C)	If increasing, the expression intensity will increase, but the ring radius will decease and the band width will not change.	Related to the production and dissociation of CI	The production rate of CI is easily tuned
(kI₀)/(b_RK)	If increasing, the ring radius and the band width will increase, leaving the expression amplitude unchanged.	Related to the light intensity emitted by sender cells and the activation rate, light sensitivity, and binding efficiency of Luminesensor.	Light intensity could be tuned, although the effect may noe be obvious experimentally.
LacI and LacIM1 related parameters	Tend to influence all three criteria.	Related to the production and dissociation rate and binding efficiency of LacI and LaciM1.	Tuning is not useful to make a better pattern.

As we can see, a_G/r_G, a_C/(b_C*r_C), and (k*I₀)/(b_R*K) are the most important and accessible parameters for pattern formation. To make it clear, we tuned several of the parameters each in one of the three groups to see the effect on pattern formation, while holding other parameters unchanged.

Firstly, we tuned a_G, the production rate of GFP:

Figure 3. Ring Pattern Simulation for a_G=1x10^-6M/min.

Figure 4. Ring Pattern Simulation for a_G=2x10^-6M/min.

Figure 5. Ring Pattern Simulation for a_G=4x10^-6M/min.

Then, we tuned a_C, the production rate of CI:

Figure 6. Ring Pattern Simulation for a_C=0.2x10^-6M/min.

Figure 7. Ring Pattern Simulation for a_C=2x10^-6M/min.

Figure 8. Ring Pattern Simulation for a_C=20x10^-6M/min.

Ultimately, we tuned I₀/K, the ratio of central light intensity to the sensitivity of Luminesensor:

Figure 9. Ring Pattern Simulation for I₀/K=1x10^-2M/min.

Figure 10. Ring Pattern Simulation for I₀/K=1x10^-1M/min.

Figure 11. Ring Pattern Simulation for I₀/K=1x10⁰M/min.

Reference

1. Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. Nature, vol.434: 1130: 1134

@@ Line 1: / Line 1: @@
 <html></p></html>{{Template:Peking2012_Color_Prologue}}{{Template:Peking2012_Color_Modeling}}<html>
 <script type="text/javascript">
-sublists_Now = 2;
+sublists_Now = 3;
 var subsubitem=subfirst.getElementsByTagName('ul')[sublists_Now].getElementsByTagName('a')[1];
 subsubitem.style.color='#60b0f0';