Team:Peking/Modeling/Phototaxis/Hexagon
From 2012.igem.org
m |
m |
||
| Line 13: | Line 13: | ||
</p> | </p> | ||
<div class="floatC"> | <div class="floatC"> | ||
| - | <img src=" | + | <img src="/wiki/images/0/0d/Peking2012_Hexagon.png" alt="" style="width:500px;"/> |
| - | <p class="description" style="width: | + | <p class="description" style="width:400px;">Figure 1. Hexagonal Closest Packing on a plane</p> |
</div> | </div> | ||
</div> | </div> | ||
| Line 68: | Line 68: | ||
</p> | </p> | ||
<div class="floatC"> | <div class="floatC"> | ||
| - | <img src=" | + | <img src="/wiki/images/1/1a/Peking2012_Hexagon_Integration.png" alt="" style="width:500px;"/> |
| - | <p class="description" style="width:500px;">Figure 2. Integral Sum. The red boundary shows the adjacent cells we sum to replace the integration with the given distance | + | <p class="description" style="width:500px;">Figure 2. Integral Sum. The red boundary shows the adjacent cells we sum to replace the integration with the given distance 5.</p> |
</div> | </div> | ||
<p> | <p> | ||
Revision as of 16:26, 23 October 2012
Appendix: Hexagonal Mesh
The Simulation Program in Hexagonal Mesh was originally designed for Turing Pattern Formation in this project. This subject was abandoned later due to the complexity of Turing System in our plan. However, the program remained, and was additionally developed for dynamic system simulation on a 2D plane.

Figure 1. Hexagonal Closest Packing on a plane
Basic Elements
At first, we considered about a dish filled with a layer of close-packed cells. The cells could communicate with each other with both in light and chemical ways. To simplify the simulation, we prefered periodic structure as the calculating chunks. Then the closest packing structure went to the hexagonal structure.
So we constructed this Hexagonal Mesh Simulating Program. To make it simulate our pattern system, we established modules for differentiation and integration.
Module 1: Differentiation
As for the chemical signal, the diffusion equation is the most common one to use.

where
- ρ(x,t) : component concentration
- t : time
- μ : the diffusion rate
By the defination of the partial differentiation, we have
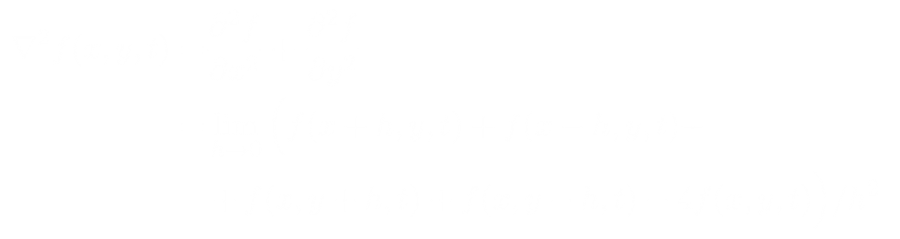
In hexagonal mesh, the expression should become
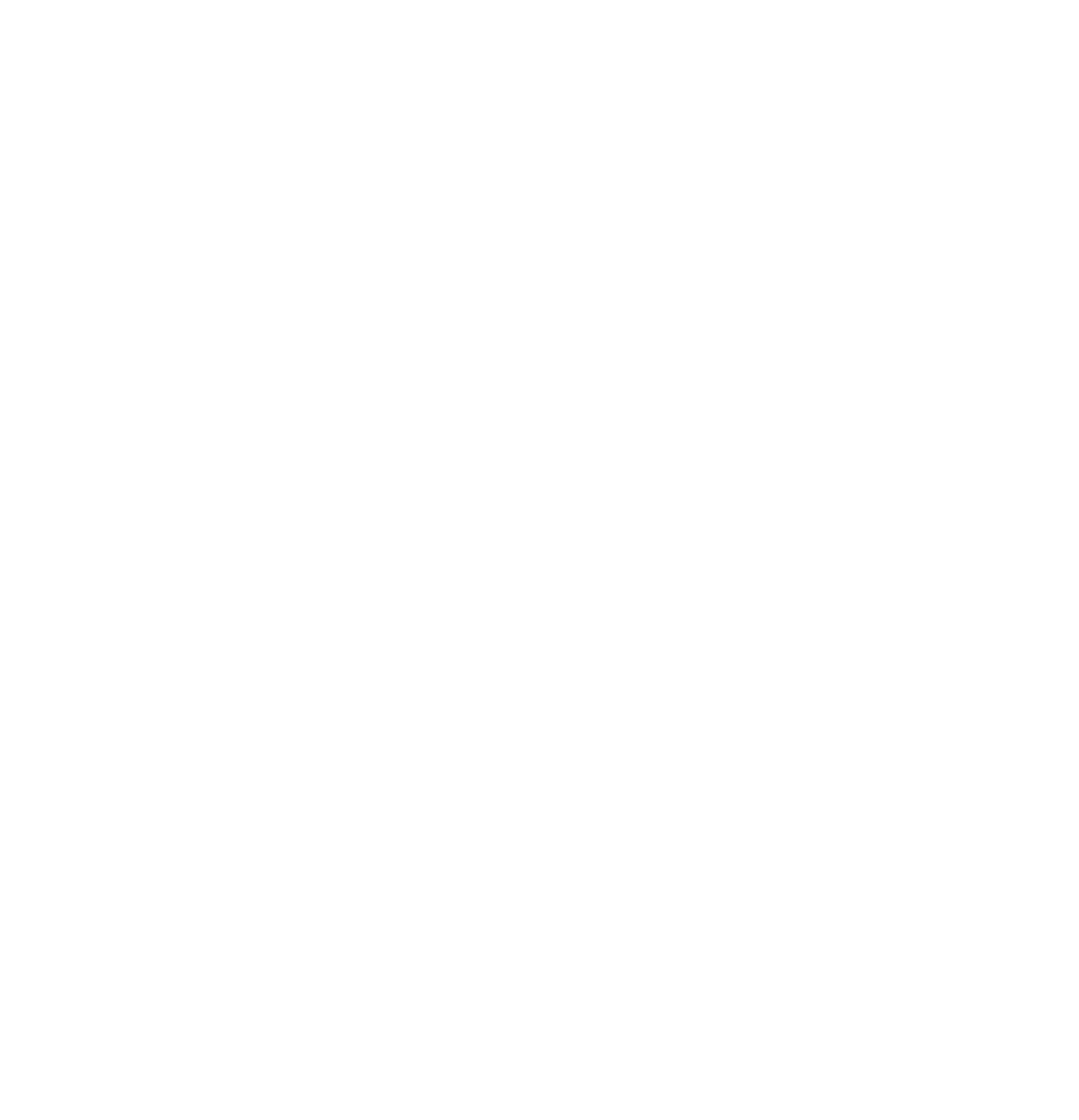
So we have
Thus we proved the validity of numeric calculation method for diffusion in hexagonal mesh.
Module 2: Integration
The essence of integration is integral sum. If the interand contributes little when the position variable approaching infinite point, the integration can be approximately replaced by finite sum of influence by the sources around.
In the abandoned system, the expression of light signal is denoted by an integration item. For approximation, we sum the adjacent cells within a given distance to replace the integration.
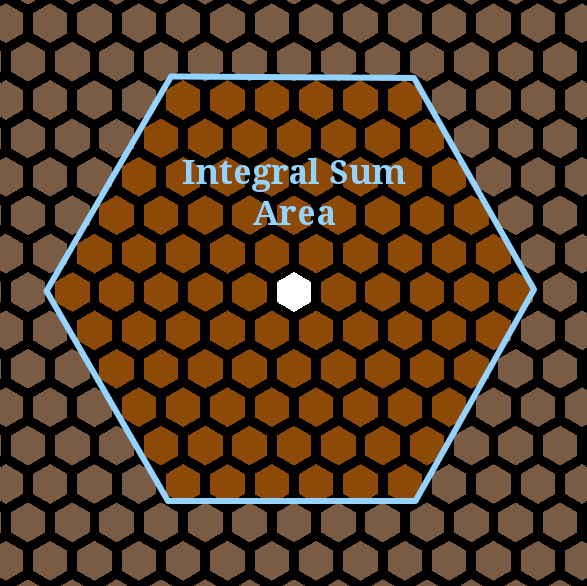
Figure 2. Integral Sum. The red boundary shows the adjacent cells we sum to replace the integration with the given distance 5.
In this way, we calculate the integration in hexagonal mesh.
Conclusion
With the notions above, we constructed the simulating program in hexagonal mesh, which is used in the simulation of phototaxis system. This program can be used for simulations for other 2D dynamic systems under small modifications. We wish this program to contribute in future works.
 "
"