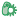Team:Peking/Modeling/Ring/Simulation
From 2012.igem.org
m |
|||
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
<html></p></html>{{Template:Peking2012_Color_Prologue}}{{Template:Peking2012_Color_Modeling}}<html> | <html></p></html>{{Template:Peking2012_Color_Prologue}}{{Template:Peking2012_Color_Modeling}}<html> | ||
<script type="text/javascript"> | <script type="text/javascript"> | ||
| - | sublists_Now = | + | sublists_Now = 3; |
var subsubitem=subfirst.getElementsByTagName('ul')[sublists_Now].getElementsByTagName('a')[1]; | var subsubitem=subfirst.getElementsByTagName('ul')[sublists_Now].getElementsByTagName('a')[1]; | ||
subsubitem.style.color='#60b0f0'; | subsubitem.style.color='#60b0f0'; | ||
| Line 10: | Line 10: | ||
<h3 id="title1">ODE Model</h3> | <h3 id="title1">ODE Model</h3> | ||
<p> | <p> | ||
| - | According to the previous circuit and ODE model, we listed all the differential equations <!--(<a href="/Team:Peking/Modeling/Appendix/ODE">detail here</a>)--> and simulated this system | + | According to the previous circuit and ODE model, we listed all the differential equations <!--(<a href="/Team:Peking/Modeling/Appendix/ODE">detail here</a>)--> and simulated this system in MATLAB with equations listed as below: |
</p> | </p> | ||
<div class="floatC"> | <div class="floatC"> | ||
| Line 17: | Line 17: | ||
<br /><br /> | <br /><br /> | ||
<div class="floatC"> | <div class="floatC"> | ||
| - | <img src="/wiki/images/ | + | <img src="/wiki/images/e/ee/Peking2012_Formula015.png" alt="Formulae" style="width:400px;"/> |
</div> | </div> | ||
<p> | <p> | ||
| - | + | We applied the inverse square law to describe the light intensity distribution on the plate according to different radius, with a central intensity <i>I<sub>0</sub></i> in a region of <i>r=1mm</i>. Here, parameters are: | |
</p> | </p> | ||
<div class="floatC"> | <div class="floatC"> | ||
| Line 27: | Line 27: | ||
<td>Parameter</td><td>Value</td><td>Unit</td><td>Description</td><td>Source</td> | <td>Parameter</td><td>Value</td><td>Unit</td><td>Description</td><td>Source</td> | ||
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>α<sub>G</sub></td><td>2</td><td>10<sup>-6</sup>M/min</td><td>GFP production rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>α<sub>C</sub></td><td>2</td><td>10<sup>-6</sup>M/min</td><td>CI production rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>α<sub>L1</sub></td><td>1</td><td>10<sup>-6</sup>M/min</td><td>LacI production rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>α<sub>L2</sub></td><td>1</td><td>10<sup>-6</sup>M/min</td><td>LacIM1 production rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>θ<sub>C</sub></td><td>8.x10<sup>-3</sup></td><td>10<sup>-6</sup>M</td><td>Binding strength of CI on LacI operator</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>θ<sub>L</sub></td><td>8.x10<sup>-1</sup></td><td>10<sup>-6</sup>M</td><td>Binding strength of LacI or LacIM1 on GFP operator</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>θ<sub>R</sub></td><td>1.x10<sup>-2</sup></td><td>10<sup>-6</sup>M</td><td>Binding strength of <i>Luminesensor</i> on corresponding operator</td><td></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>γ<sub>G</sub></td><td>6.92x10<sup>-2</sup></td><td>min<sup>-1</sup></td><td>GFP dissociation rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>γ<sub>C</sub></td><td>6.92x10<sup>-2</sup></td><td>min<sup>-1</sup></td><td>CI dissociation rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>γ<sub>L</sub></td><td>2.31x10<sup>-2</sup></td><td>min<sup>-1</sup></td><td>LacI and LacIM1 dissociation rate constant</td><td><a href="#ref1" title="Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. <i>Nature</i>, vol.434: 1130: 1134">[1]</a></td> |
| - | + | ||
| - | + | ||
</tr><tr> | </tr><tr> | ||
<td>I<sub>0</sub></td><td>1000</td><td>AU</td><td>Maximum light intensity in the middle of the plate </td><td></td> | <td>I<sub>0</sub></td><td>1000</td><td>AU</td><td>Maximum light intensity in the middle of the plate </td><td></td> | ||
| Line 53: | Line 51: | ||
<td>k</td><td>500</td><td>10<sup>-6</sup>M</td><td><i>Luminesensor</i> activation rate under light</td><td></td> | <td>k</td><td>500</td><td>10<sup>-6</sup>M</td><td><i>Luminesensor</i> activation rate under light</td><td></td> | ||
</tr><tr> | </tr><tr> | ||
| - | <td>K</td><td>10000</td><td>AU</td><td> | + | <td>K</td><td>10000</td><td>AU</td><td>Light sensitivity of <i>Luminesensor</i> activation </td><td></td> |
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<p> | <p> | ||
| - | The simulation | + | The simulation results in static state are shown below: |
</p> | </p> | ||
<div class="floatC"> | <div class="floatC"> | ||
| Line 71: | Line 69: | ||
</div> | </div> | ||
<p> | <p> | ||
| - | From the Figure 1 above, we | + | From the Figure 1 & 2 above, we discover that, with wildtype parameters, ring-like pattern is formed based on sender-receiver communication through bio-luminescence. |
</p> | </p> | ||
</div> | </div> | ||
| Line 78: | Line 76: | ||
<h3 id="title2">Parameter Analysis</h3> | <h3 id="title2">Parameter Analysis</h3> | ||
<p> | <p> | ||
| - | After modeling the | + | After modeling the ring-like pattern formation with wildtype parameters, we attempted to optimize it in a rational way. We have tuned the parameters both up and down, one by one, and finally discovered several parameters which predominantly influence the expression intensity, ring radius, and band width of pattern formation. |
</p> | </p> | ||
<table style="width:600px;"><tr> | <table style="width:600px;"><tr> | ||
| - | |||
<td>Parameter</td> | <td>Parameter</td> | ||
| + | <td>Function</td> | ||
<td>Description</td> | <td>Description</td> | ||
<td>Remark</td> | <td>Remark</td> | ||
</tr><tr> | </tr><tr> | ||
| - | <td | + | <td>α<sub>G</sub>/γ<sub>G</sub></td><td>If increasing, the expression intensity will be amplified, but the ring radius and the band width will not change. </td><td>Related to the production and dissociation of GFP</td><td>The production rate of GFP is easily tuned.</td> |
| - | + | ||
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>α<sub>C</sub>/(θ<sub>C</sub>*γ<sub>C</sub>)</td><td>If increasing, the expression intensity will increase, but the ring radius will decease and the band width will not change. </td><td>Related to the production and dissociation of CI</td><td>The production rate of CI is easily tuned</td> |
</tr><tr> | </tr><tr> | ||
| - | <td | + | <td>(k*I<sub>0</sub>)/(θ<sub>R</sub>*K)</td><td>If increasing, the ring radius and the band width will increase, leaving the expression amplitude unchanged. </td><td>Related to the light intensity emitted by sender cells and the activation rate, light sensitivity, and binding efficiency of <i>Luminesensor</i>. </td><td>Light intensity could be tuned, although the effect may noe be obvious experimentally.</td> |
| - | + | ||
</tr><tr> | </tr><tr> | ||
| - | <td> | + | <td>LacI and LacIM1 related parameters</td><td>Tend to influence all three criteria.</td><td>Related to the production and dissociation rate and binding efficiency of LacI and LaciM1. </td><td>Tuning is not useful to make a better pattern.</td> |
</tr></table> | </tr></table> | ||
| - | + | <p> | |
| + | As we can see, α<sub>G</sub>/γ<sub>G</sub>, α<sub>C</sub>/(θ<sub>C</sub>*γ<sub>C</sub>), and (k*I<sub>0</sub>)/(θ<sub>R</sub>*K) are the most important and accessible parameters for pattern formation. To make it clear, we tuned several of the parameters each in one of the three groups to see the effect on pattern formation, while holding other parameters unchanged. | ||
| + | <br /><br /> | ||
| + | Firstly, we tuned α<sub>G</sub>, the production rate of GFP: | ||
| + | </p> | ||
| + | <div class="floatC"> | ||
| + | <img src="/wiki/images/4/4e/G(1).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 3. Ring Pattern Simulation for <i>α<sub>G</sub>=1x10<sup>-6</sup>M/min</i>. | ||
| + | </p> | ||
| + | <img src="/wiki/images/3/31/G(2).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 4. Ring Pattern Simulation for <i>α<sub>G</sub>=2x10<sup>-6</sup>M/min</i>. | ||
| + | </p> | ||
| + | <img src="/wiki/images/5/59/G(4).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 5. Ring Pattern Simulation for <i>α<sub>G</sub>=4x10<sup>-6</sup>M/min</i>. | ||
| + | </p> | ||
| + | </div> | ||
| + | <p> | ||
| + | Then, we tuned α<sub>C</sub>, the production rate of CI: | ||
| + | </p> | ||
| + | <div class="floatC"> | ||
| + | <img src="/wiki/images/5/55/C(0.2).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 6. Ring Pattern Simulation for <i>α<sub>C</sub>=0.2x10<sup>-6</sup>M/min</i>. | ||
| + | </p> | ||
| + | <img src="/wiki/images/8/83/C(2).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 7. Ring Pattern Simulation for <i>α<sub>C</sub>=2x10<sup>-6</sup>M/min</i>. | ||
| + | </p> | ||
| + | <img src="/wiki/images/b/bd/C(20).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 8. Ring Pattern Simulation for <i>α<sub>C</sub>=20x10<sup>-6</sup>M/min</i>. | ||
| + | </p> | ||
| + | </div> | ||
| + | <p> | ||
| + | Ultimately, we tuned I<sub>0</sub>/K, the ratio of central light intensity to the sensitivity of <i>Luminesensor</i>: | ||
| + | </p> | ||
| + | <div class="floatC"> | ||
| + | <img src="/wiki/images/c/c1/I0(0.01).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 9. Ring Pattern Simulation for <i>I<sub>0</sub>/K=1x10<sup>-2</sup>M/min</i>. | ||
| + | </p> | ||
| + | <img src="/wiki/images/5/5a/I0(0.1).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 10. Ring Pattern Simulation for <i>I<sub>0</sub>/K=1x10<sup>-1</sup>M/min</i>. | ||
| + | </p> | ||
| + | <img src="/wiki/images/b/ba/I0(1).png" alt="Simulation Result" style="width:500px;"/> | ||
| + | <p class="description" style="text-align:center;"> | ||
| + | Figure 11. Ring Pattern Simulation for <i>I<sub>0</sub>/K=1x10<sup>0</sup>M/min</i>. | ||
| + | </p> | ||
| + | </div> | ||
</div> | </div> | ||
| - | |||
| - | |||
<div class="PKU_context floatR"> | <div class="PKU_context floatR"> | ||
<h3 id="title4">Reference</h3> | <h3 id="title4">Reference</h3> | ||
Latest revision as of 12:23, 26 October 2012
ODE Model
According to the previous circuit and ODE model, we listed all the differential equations and simulated this system in MATLAB with equations listed as below:
We applied the inverse square law to describe the light intensity distribution on the plate according to different radius, with a central intensity I0 in a region of r=1mm. Here, parameters are:
| Parameter | Value | Unit | Description | Source |
| αG | 2 | 10-6M/min | GFP production rate constant | [1] |
| αC | 2 | 10-6M/min | CI production rate constant | [1] |
| αL1 | 1 | 10-6M/min | LacI production rate constant | [1] |
| αL2 | 1 | 10-6M/min | LacIM1 production rate constant | [1] |
| θC | 8.x10-3 | 10-6M | Binding strength of CI on LacI operator | [1] |
| θL | 8.x10-1 | 10-6M | Binding strength of LacI or LacIM1 on GFP operator | [1] |
| θR | 1.x10-2 | 10-6M | Binding strength of Luminesensor on corresponding operator | |
| γG | 6.92x10-2 | min-1 | GFP dissociation rate constant | [1] |
| γC | 6.92x10-2 | min-1 | CI dissociation rate constant | [1] |
| γL | 2.31x10-2 | min-1 | LacI and LacIM1 dissociation rate constant | [1] |
| I0 | 1000 | AU | Maximum light intensity in the middle of the plate | |
| k | 500 | 10-6M | Luminesensor activation rate under light | |
| K | 10000 | AU | Light sensitivity of Luminesensor activation |
The simulation results in static state are shown below:
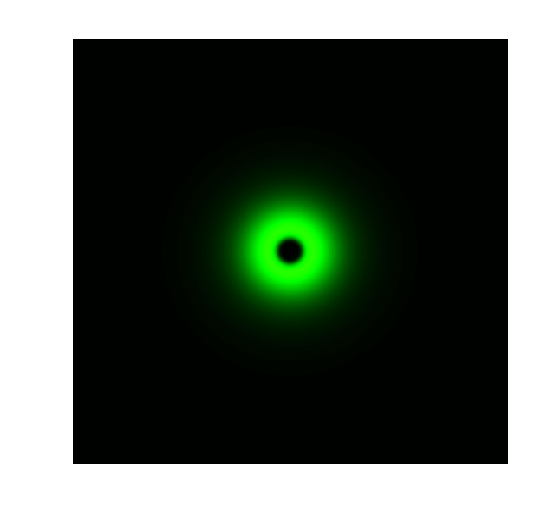
Figure 1. ODE Simulation in a plate of the ring-like pattern formation.
Figure 2. ODE Simulation for the radial expression amplitude of the ring-like pattern formation.
From the Figure 1 & 2 above, we discover that, with wildtype parameters, ring-like pattern is formed based on sender-receiver communication through bio-luminescence.
Parameter Analysis
After modeling the ring-like pattern formation with wildtype parameters, we attempted to optimize it in a rational way. We have tuned the parameters both up and down, one by one, and finally discovered several parameters which predominantly influence the expression intensity, ring radius, and band width of pattern formation.
| Parameter | Function | Description | Remark |
| αG/γG | If increasing, the expression intensity will be amplified, but the ring radius and the band width will not change. | Related to the production and dissociation of GFP | The production rate of GFP is easily tuned. |
| αC/(θC*γC) | If increasing, the expression intensity will increase, but the ring radius will decease and the band width will not change. | Related to the production and dissociation of CI | The production rate of CI is easily tuned |
| (k*I0)/(θR*K) | If increasing, the ring radius and the band width will increase, leaving the expression amplitude unchanged. | Related to the light intensity emitted by sender cells and the activation rate, light sensitivity, and binding efficiency of Luminesensor. | Light intensity could be tuned, although the effect may noe be obvious experimentally. |
| LacI and LacIM1 related parameters | Tend to influence all three criteria. | Related to the production and dissociation rate and binding efficiency of LacI and LaciM1. | Tuning is not useful to make a better pattern. |
As we can see, αG/γG, αC/(θC*γC), and (k*I0)/(θR*K) are the most important and accessible parameters for pattern formation. To make it clear, we tuned several of the parameters each in one of the three groups to see the effect on pattern formation, while holding other parameters unchanged.
Firstly, we tuned αG, the production rate of GFP:
.png)
Figure 3. Ring Pattern Simulation for αG=1x10-6M/min.
.png)
Figure 4. Ring Pattern Simulation for αG=2x10-6M/min.
.png)
Figure 5. Ring Pattern Simulation for αG=4x10-6M/min.
Then, we tuned αC, the production rate of CI:
.png)
Figure 6. Ring Pattern Simulation for αC=0.2x10-6M/min.
.png)
Figure 7. Ring Pattern Simulation for αC=2x10-6M/min.
.png)
Figure 8. Ring Pattern Simulation for αC=20x10-6M/min.
Ultimately, we tuned I0/K, the ratio of central light intensity to the sensitivity of Luminesensor:
.png)
Figure 9. Ring Pattern Simulation for I0/K=1x10-2M/min.
.png)
Figure 10. Ring Pattern Simulation for I0/K=1x10-1M/min.
.png)
Figure 11. Ring Pattern Simulation for I0/K=1x100M/min.
Reference
- 1. Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. Nature, vol.434: 1130: 1134
 "
"