Team:Peking/Modeling/Ring/Simulation
From 2012.igem.org
| Line 51: | Line 51: | ||
<td>k</td><td>500</td><td>10<sup>-6</sup>M</td><td><i>Luminesensor</i> activation rate under light</td><td></td> | <td>k</td><td>500</td><td>10<sup>-6</sup>M</td><td><i>Luminesensor</i> activation rate under light</td><td></td> | ||
</tr><tr> | </tr><tr> | ||
| - | <td>K</td><td>10000</td><td>AU</td><td> | + | <td>K</td><td>10000</td><td>AU</td><td>Light sensitivity of <i>Luminesensor</i> activation </td><td></td> |
</tr> | </tr> | ||
</table> | </table> | ||
Revision as of 21:01, 24 October 2012
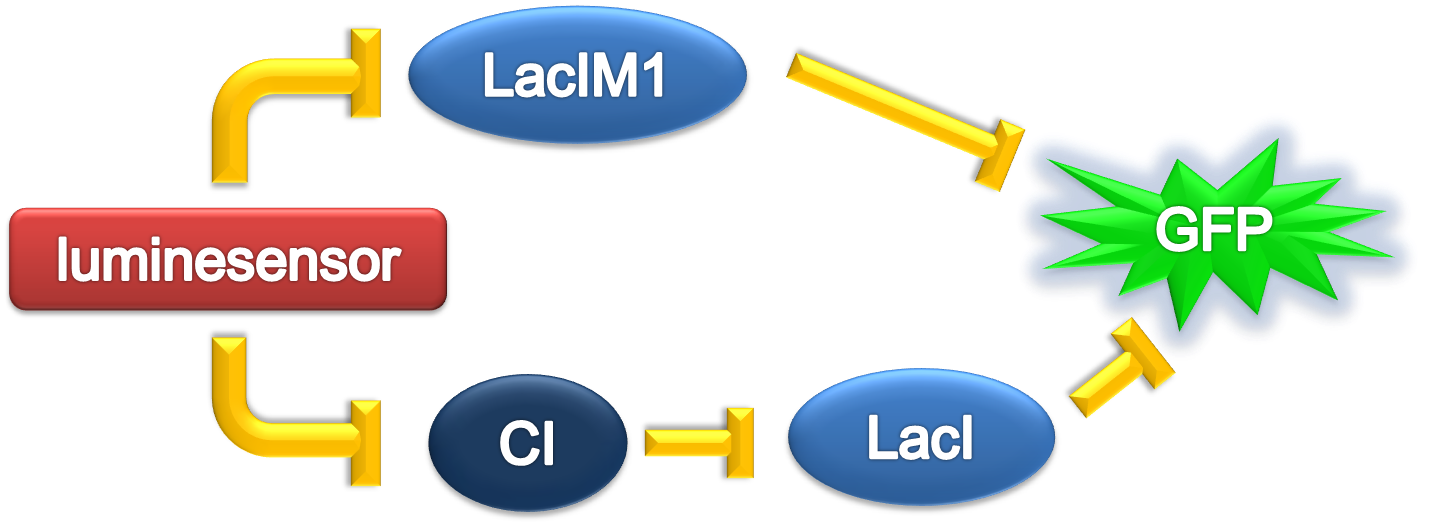
ODE Model
According to the previous circuit and ODE model, we listed all the differential equations and simulated this system in MATLAB with equations listed as below:
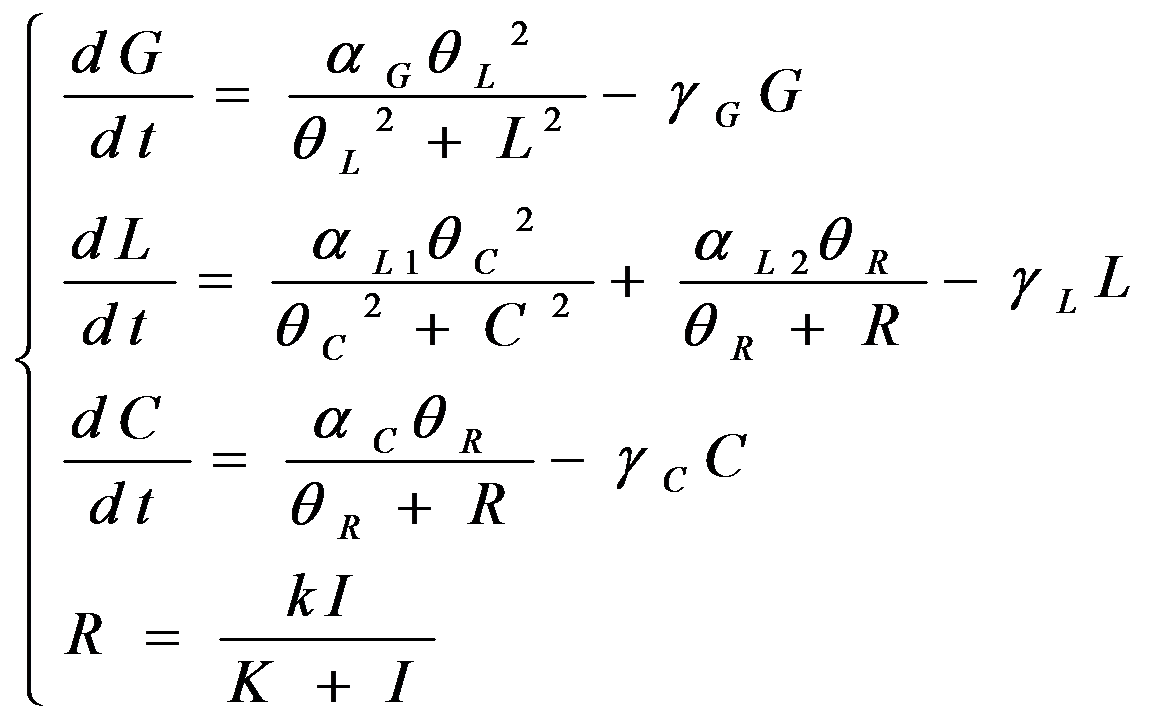
We applied the inverse square law to describe the light intensity distribution on the plate according to different radius, with a central intensity I0 in a region of r=1mm. Here, parameters are:
| Parameter | Value | Unit | Description | Source |
| aG | 2 | 10-6M/min | GFP production rate constant | [1] |
| aC | 2 | 10-6M/min | CI production rate constant | [1] |
| aL1 | 1 | 10-6M/min | LacI production rate constant | [1] |
| aL2 | 1 | 10-6M/min | LacIM1 production rate constant | [1] |
| bC | 8.x10-3 | 10-6M | Binding strength of CI on LacI operator | [1] |
| bL | 8.x10-1 | 10-6M | Binding strength of LacI or LacIM1 on GFP operator | [1] |
| bR | 1.x10-2 | 10-6M | Binding strength of Luminesensor on corresponding operator | |
| rG | 6.92x10-2 | min-1 | GFP dissociation rate constant | [1] |
| rC | 6.92x10-2 | min-1 | CI dissociation rate constant | [1] |
| rL | 2.31x10-2 | min-1 | LacI and LacIM1 dissociation rate constant | [1] |
| I0 | 1000 | AU | Maximum light intensity in the middle of the plate | |
| k | 500 | 10-6M | Luminesensor activation rate under light | |
| K | 10000 | AU | Light sensitivity of Luminesensor activation |
The simulation results in static state are shown below:
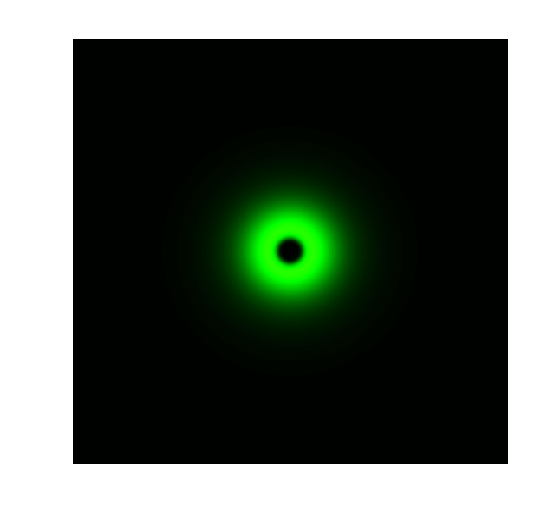
Figure 1. ODE Simulation in a plate of the ring-like pattern formation.
Figure 2. ODE Simulation for the radial expression amplitude of the ring-like pattern formation.
From the Figure 1 & 2 above, we discover that, with wildtype parameters, ring-like pattern is formed based on sender-receiver communication through bio-luminescence.
Parameter Analysis
After modeling the ring-like pattern formation with wildtype parameters, we attempted to optimize it in a rational way. We have tuned the parameters both up and down, one by one, and finally discovered five parameters which predominantly influence the expression intensity, ring radius, and band width of pattern formation.
| Function | Parameter | Description | Remark |
| Reduce responsing time | k1 | Vivid lighting decay rate constant | Mainly on process from Light to Dark |
| k3 | rate constant of monomer LexA releasing from specific binding site | ||
| Enhance contrast | K2 | Vivid association equilibrium constant | More dimerization provides more binding opportunity |
| K5 | dimered LexA binding equilibrium constant | More binding affinity |
Reference
- 1. Subhayu Basu et al.(2005), A synthetic multicellular system for programmed pattern formation. Nature, vol.434: 1130: 1134
 "
"