Team:TU Munich/Modeling/Priors

From 2012.igem.org

Contents

Prior Data

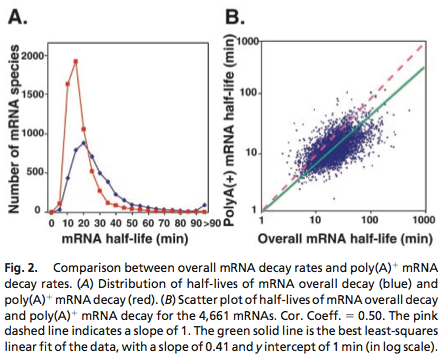
Yeast mRNA Degradation Rate

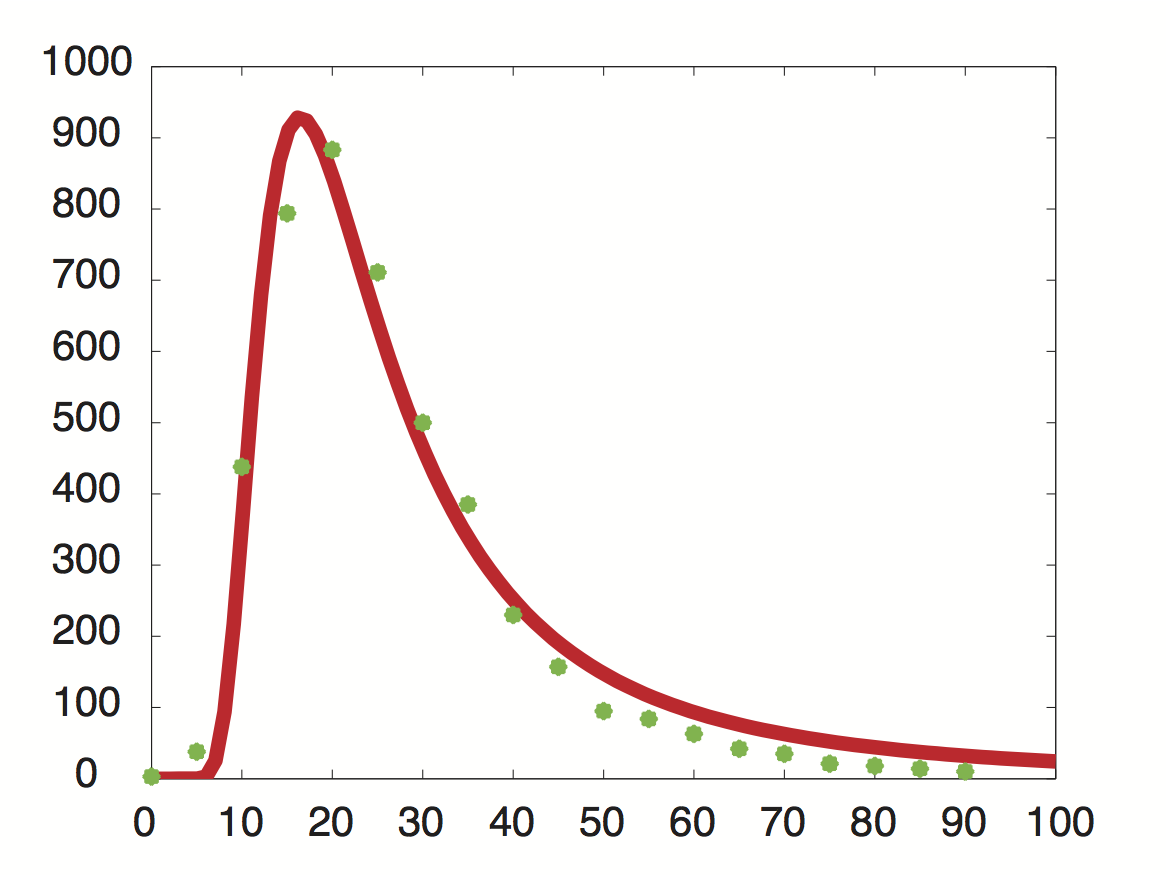
Fig. 1 Genome-wide mRNA decay rate. Picture taken from Wang et. al. 2002
Fig. 2 Approximated probability density for the genome-wide mRNA decay rate.

Data was obtained from the Paper http://www.ncbi.nlm.nih.gov/pubmed/11972065 Wang et al., 2002 and processed by http://arohatgi.info/webplotdigitizer/app/ Rohatgi, 2012 to obtain raw data. Using a least-squared error approximation the distribution of the half life time in was approximated as noncentral t-distribution with parameters μ = 1.769 and ν = 20.59. 

dataGraph = [
0.0018691649126431735,0.0016851538590669062
0.05978099456360327,0.01885629059542104
0.11548146330755026,0.21910551258377348
0.17122389948476902,0.396902157771723
0.2253457470848775,0.4417136917136917
0.2815821076690642,0.3552607791738227
0.3359848142456839,0.249812760682326
0.39216629434020744,0.19272091011221448
0.4465173486912618,0.11490683229813668
0.5026600896166115,0.07854043723608946
0.5569239808370243,0.04735863431515607
0.6111394480959699,0.04208365077930302
0.667233765059852,0.031624075102336016
0.7233280820237343,0.021164499425369035
0.777540321018582,0.017616637181854626
0.8373665112795547,0.010604847561369285
0.8897063570976615,0.008787334874291503
0.9420462029157682,0.006969822187213598
0.9999935434718044,0.005142624707842157
];
%scale the data
X = round(dataGraph(:,1)*90);
y = round(dataGraph(:,2)*2000);

k(1) = 1.769292045467269;
k(2) = 20.589996419308118;
k(3) = 24852.48237036381;

k=fminunc(@(z) sum((y-z(3)*nctpdf(X,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*nctpdf(X,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*nctpdf(X,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*nctpdf(X,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*nctpdf(X,z(1),z(2))).^2),k);

The matlab nctpdf.m script needs to compute the limit of an infinite series to calculate the probabilities for the noncentral t-distribution. As this the function will be called several million times during the generation of samples, the computation was quite time consuming and the funtion was approximated using chebyshev interpolation http://www2.maths.ox.ac.uk/chebfun/ Trefethen, 2012.

Yeast Protein Degradation Rate

For the Degradation Rate the N-end rule http://www.ncbi.nlm.nih.gov/pubmed/9112437 Varshavsky, 1997 served as approximation for the half life time. It states that the half life time in S. cerevisiae can be approximated based on the amino acid after the initial start codon.

Residue ! Half-life
Arg 2 min
Lys, Phe, Leu, Trp, His, Asp, Asn 3 min
Tyr, Gln 10 min
Ile, Glu 30 min
Pro > 5 h
Cys, Ala, Ser, Thr, Gly, Val, Met > 30 h

As these values do not give enough information to infer a proper distribution, only the two lower bounds 5 h and 30 h will serve as approximate lower bounds for the optimization routines.

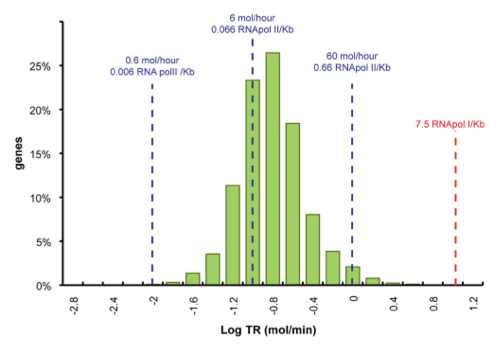
Yeast Transcription Rate

Fig. 3 Genome-wide transcription rate. Picture taken from Pelechano et al. 2010
Fig. 4 Approximated probability density for the genome-wide transcription rate.

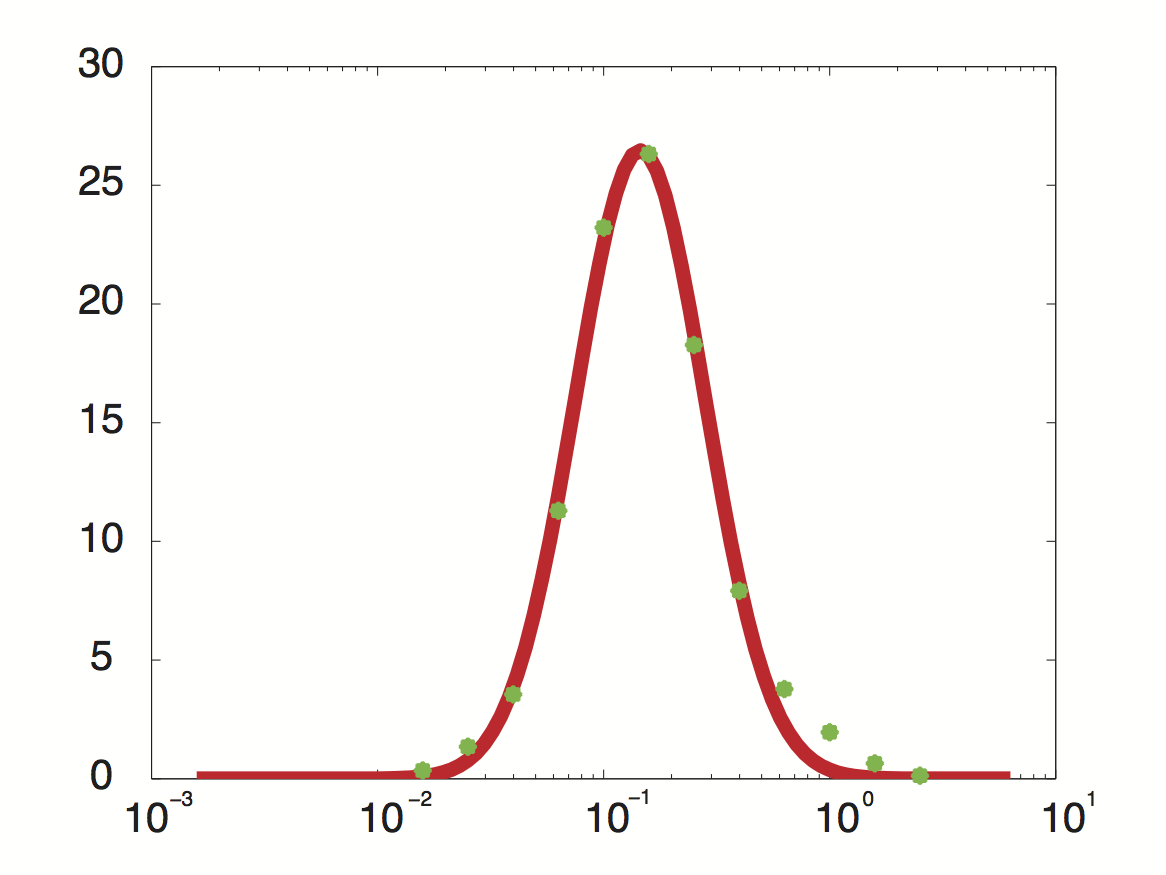
Data was obtained from the Paper http://www.ncbi.nlm.nih.gov/pubmed/21103382 Pelechano et al., 2010 and processed by http://arohatgi.info/webplotdigitizer/app/ Rohatgi, 2012 to obtain raw data. Using a least-squared error approximation the distribution of the transcription rate was approximated as log-normal distribution with parameters μ = -1.492 and σ = 0.661;. 

dataGraph = [
-1.8,0.3442950751957339
-1.6,1.3525375039897853
-1.4,3.5492668181220783
-1.2,11.28874786429094
-1.0,23.213749272450762
-0.8,26.31522126884587
-0.6,18.273455248681024
-0.4,7.913623476840467
-0.2,3.7755111620134825
0,1.9559339854677913
0.2,0.6458759692833385
0.4,0.12767315671880167
];

x = 10.^dataGraph(:,1);
y = dataGraph(:,2);

k(1) = -0.8;
k(2) = 0.2;
k(3) = 25;

k=fminunc(@(z) sum((y-z(3)*lognpdf(x,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*lognpdf(x,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*lognpdf(x,z(1),z(2))).^2),k);
k=fminunc(@(z) sum((y-z(3)*lognpdf(x,z(1),z(2))).^2),k);

Reference

Retrieved from "http://2012.igem.org/Team:TU_Munich/Modeling/Priors"