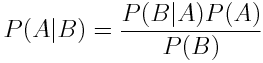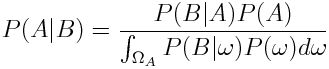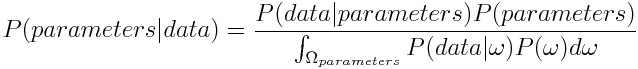Team:TU Munich/Modeling/Methods
From 2012.igem.org
(→Derivation) |
(→Monte Carlo Methods) |
||
| Line 68: | Line 68: | ||
== Monte Carlo Methods == | == Monte Carlo Methods == | ||
---- | ---- | ||
| + | |||
| + | Usually it is not possible to give any closed expression for the posterior distribution. When working with high dimensional posteriors where the location of the support of the distribution is not clear Interpolat Hence alternative methods are necessary ([http://www.inference.phy.cam.ac.uk/mackay/itila/book.html David MacKay 2003]) | ||
=== Metropolis Hastings === | === Metropolis Hastings === | ||
Revision as of 18:50, 10 September 2012



Contents |
Modeling Methods
Why Mathematical Models
To be able to predict the behavior of a given biological system, one has to create a mathematical model of the system. The model is usually generated according to the Law of Mass Action[reference] and then simplified by assuming certain reactions to be fast. This model then could e.g. facilitate optimizations of bio-synthetic pathways by regulating the relative expression levels of the involved enzymes.
Why are we not necessarily interested in the best fit
To create a model that produces quantitative predictions, one needs to tune the parameters to fit experimental data. This procedure is called inference and is usually accomplished by computing the least squares[reference] approximation of the model to the experimental data with respect to the parameters.
There are several difficulties with this approach: In the case of a non-convex least squares error function several local minima may exist and optimizations algorithms will struggle to find all of them. This means one might not be able to find the best fit or even a biologically reasonable fit.
Another issue with this approach that it gives no information on the shape of the error function in the neighborhood of the obtained fit. Although it is possible to obtain information about the curvature by computing the hessian of the error function, but this can be very computationally intensive if no analytical expression is given and only provides local information.
This poses problems if the error function is very flat. Then in the neighborhood of the set of best fit parameters, a broad range of parameters exist, that produce very similar results. This however drastically reduces the significance of the best fit parameters
What is the benefit of assuming a stochastic distribution of parameters
Usually biological systems exhibit some sort of stochasticity. If the behavior of a sufficiently large amount of cells is observed, it is justifiable to take only the mean value into consideration and thereby assume a deterministic behavior. On the one hand this means we can describe the system with ordinary and partial differential equations instead of stochastic differential equations, which reduces the computational cost of simulating the system. On the other hand this means that we lose the information we could infer from the variance of our measurements as well as higher order moments.
Assuming that parameter are distributed according to some density allows us, to deduce information from variance of measurements, while still describing the system in a deterministic fashion.
Bayesian Inference
Derivation
Bayes' Rule allow the expression of the probability of A given B in terms of the probabity of A, B and B given A.
We can remove the dependence on the probability of B by applying the law of total probability:
Now as we want to get an expression for the probability of the parameters given our measured data, we plug in parameters for A and data for B we get
As the denominator is a constant and only needed to normalize the distribution, we will omit it factor in the future.
Futhermore we will call
P(parameters|data): posterior
P(data|parameters): likelihood
P(parameters): prior
The likelihood tells us how probable it is the systems will produce the data from the experiments given the selected parameters according to our model.
The prior gives the probability of our parameters, independent of our model or our data. As the name already suggests, the prior gives the option to incorporate prior knowledge about the distribution of the parameters.
Relation to least squares
If we do not know anything about the parameters, e.g. they all have the same probability we can omit the prior. This means that the posterior is equal to the likelihood.
Now if the likelihood is a gaussian distribution, maximizing the logarithm of the likelihood, as function of the parameters, is the same as finding the least squares approximation.
Monte Carlo Methods
Usually it is not possible to give any closed expression for the posterior distribution. When working with high dimensional posteriors where the location of the support of the distribution is not clear Interpolat Hence alternative methods are necessary (David MacKay 2003)
Metropolis Hastings
Sensitivity Analysis
Vision
 "
"