Team:Calgary/Notebook/FluxAnalysis
From 2012.igem.org
| Line 6: | Line 6: | ||
</html> | </html> | ||
| - | <h2>Week | + | <h2>Week 1-3 </h2> |
<p>Refer to Hydrocarbon Modelling Part [https://2012.igem.org/wiki/index.php?title=Team:Calgary/Notebook/Hydrocarbon]</p> | <p>Refer to Hydrocarbon Modelling Part [https://2012.igem.org/wiki/index.php?title=Team:Calgary/Notebook/Hydrocarbon]</p> | ||
| + | |||
<h2>Week 4 (May 22-25)</h2> | <h2>Week 4 (May 22-25)</h2> | ||
| Line 15: | Line 16: | ||
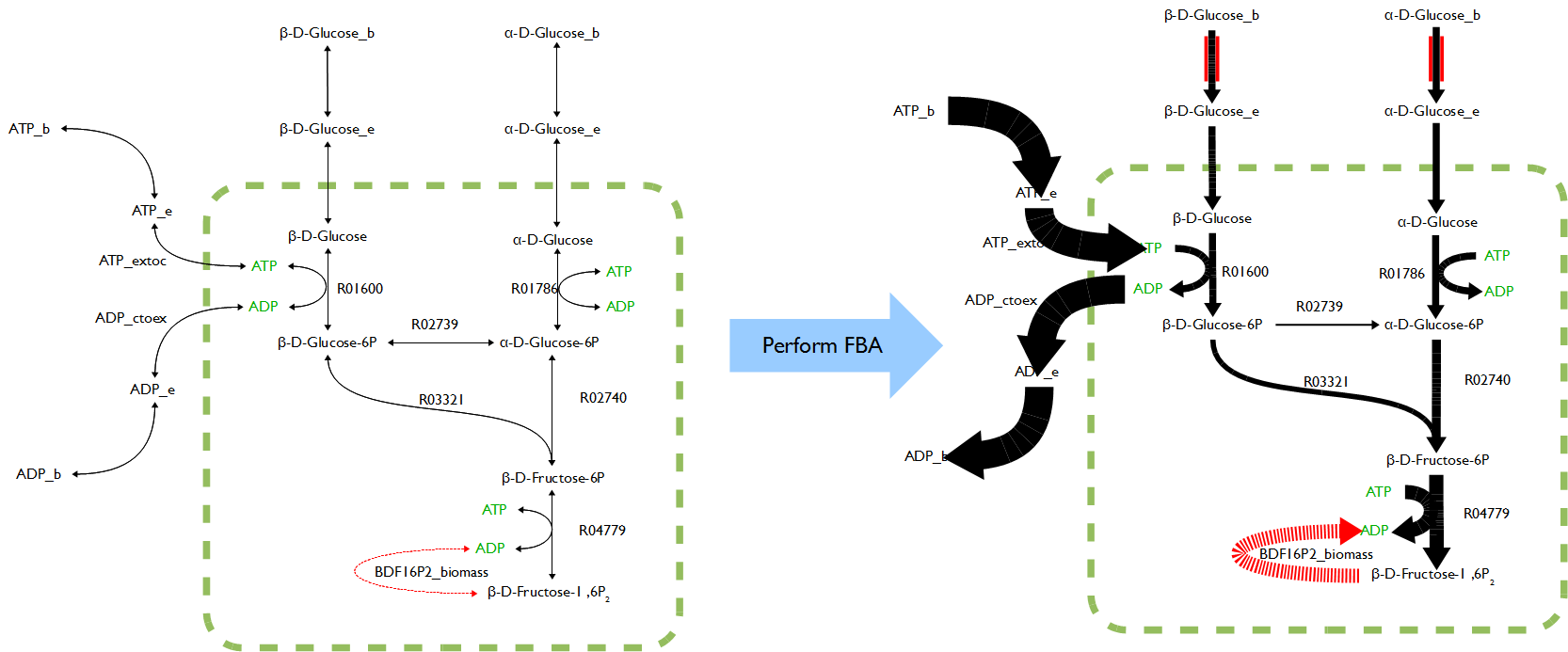
[[File:UCalgary 2012 FBAEx.png|thumb|600px|center|The results of FBA on a prepared metabolic network of the top six reactions of glycolysis. The predicted flux through each reaction is proportional to the width of the line. Objective function in red, constraints on alpha-D-Glucose and beta-D-Glucose import represented as red bars. Original: Wikipedia]] | [[File:UCalgary 2012 FBAEx.png|thumb|600px|center|The results of FBA on a prepared metabolic network of the top six reactions of glycolysis. The predicted flux through each reaction is proportional to the width of the line. Objective function in red, constraints on alpha-D-Glucose and beta-D-Glucose import represented as red bars. Original: Wikipedia]] | ||
<h5>The Steady State Assumption</h5> | <h5>The Steady State Assumption</h5> | ||
| - | <p>In chemistry, a steady state is a situation in which all state variables are constant in spite of ongoing processes that strive to change them. | + | <p>A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero. In chemistry, a steady state is a situation in which all state variables are constant in spite of ongoing processes that strive to change them. </p> |
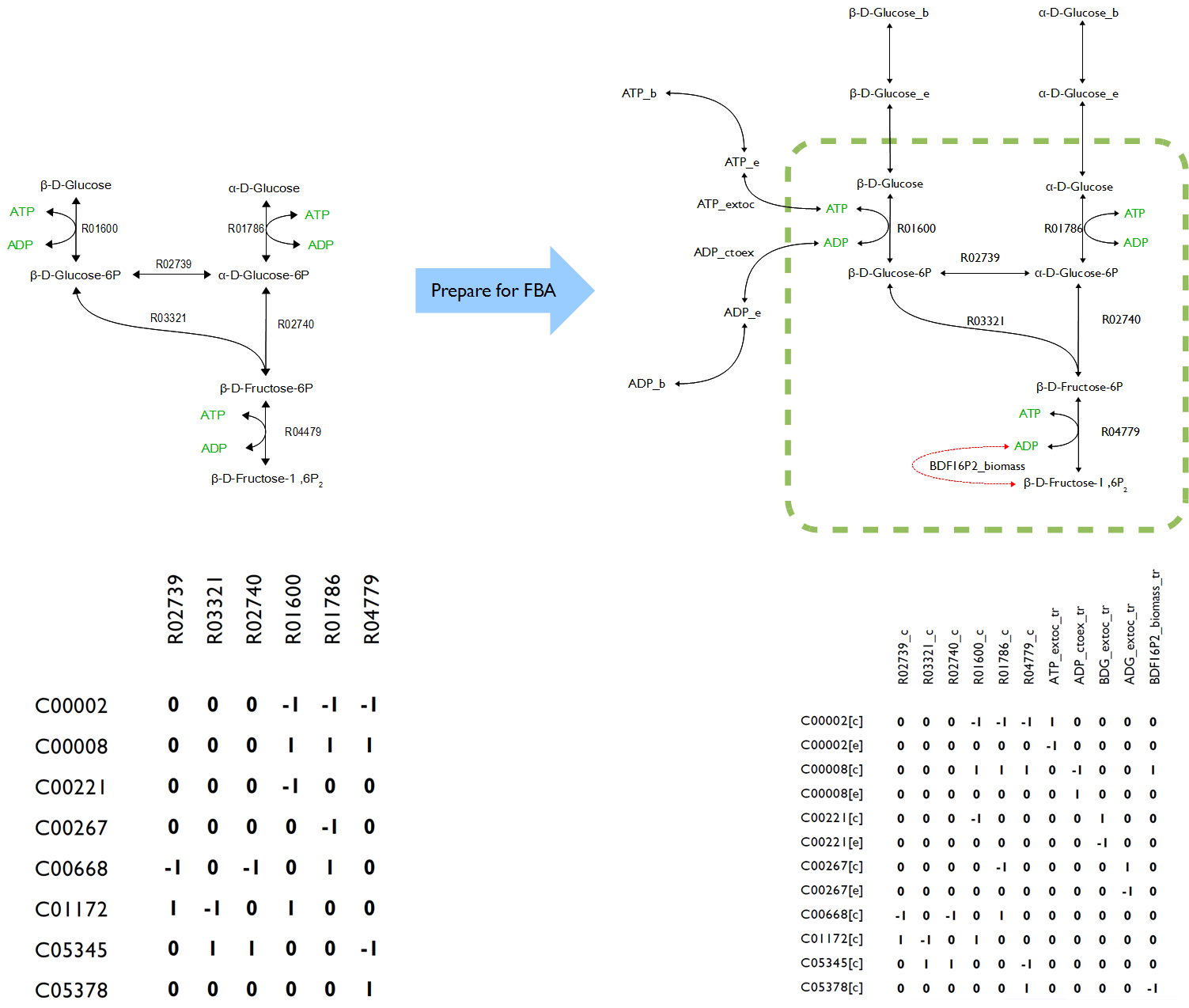
| + | <h5>Stoichiometric & Flux Matrix </h5> | ||
| + | <p>Stoichiometry is a branch of chemistry that deals with the relative quantities of reactants and products in chemical reactions. In a balanced chemical reaction, the relations among quantities of reactants and products typically form a ratio of whole numbers. | ||
| + | <br>Flux matrix, in terms of flux rate, is a rate of turnover of molecules through a reaction pathway. | ||
| + | </p> | ||
| + | [[File:UCalgary 2012 FBAexWithSMatrix.png|thumb|600px|center|An example stoichiometric matrix for a network representing the top of glycolysis and that same network after being prepared for FBA.Original:Wikipedia]] | ||
<h4> Extended Flux Analysis</h4> | <h4> Extended Flux Analysis</h4> | ||
| + | <h5>Flux variability analysis</h5> | ||
| + | <p>The optimal solution to the flux-balance problem is rarely unique with many possible, and equally optimal, solutions existing. Flux variability analysis (FVA), built-in to virtually all current analysis software, returns the boundaries for the fluxes through each reaction that can, paired with the right combination of other fluxes, produce the optimal solution. Reactions which can support a low variability of fluxes through them are likely to be of a higher importance to an organism and FVA is a promising technique for the identification of reactions that are highly important. </p> | ||
| + | <h5>Dynamic FBA</h5> | ||
| + | <p>Dynamic FBA attempts to add the ability for models to change over time, thus in some ways avoiding the strict homoeostatic condition of pure FBA. Typically the technique involves running an FBA simulation, changing the model based on the outputs of that simulation, and rerunning the simulation. By repeating this process an element of feedback is achieved over time.</p> | ||
<h4>Metabolic Network Reconstruction</h4> | <h4>Metabolic Network Reconstruction</h4> | ||
| - | <h3>Tools</h3> | + | <p>Metabolic network reconstructions are biochemically, genetically, and genomically (BiGG) structured knowledge bases that seek to formally represent the known metabolic activities of an organism. Network reconstructions also exist for other types of biological networks, including transcription/translation and signaling networks. Genome-scale metabolic networks have been reconstructed for nearly 40 organisms so far, including E. coli. These reconstructions are useful because they can be converted into constraint-based models, allowing useful predictive calculations like flux balance analysis to be performed. Constraint-based models of E. coli have existed for nearly twenty years. The first genome-scale model of E. coli metabolism was released in 2000, and this model continues to be expanded and updated today.[http://ecoliwiki.net/colipedia/index.php/Metabolic_Network_Reconstructions]</p> |
| + | Metabolic network reconstruction and simulation allows for an in depth insight into comprehending the molecular mechanisms of a particular organism, especially correlating the genome with molecular physiology (Francke, Siezen, and Teusink 2005). A reconstruction breaks down metabolic pathways into their respective reactions and enzymes, and analyzes them within the perspective of the entire network. </p> | ||
| + | <h3>Modelling</h3> | ||
| + | <h4>Constraint-based Model</h4> | ||
| + | <p>Constraint-based models are a way of mathematically encoding a metabolic network reconstruction. Networks can be encoded as stoichiometric matrices (S), in which each row represents a unique metabolite and each column represents a biochemical reaction. The entries in each column of this matrix are the stoichiometric coefficients of the metabolites in the reaction. Metabolites that are consumed have a negative coefficient and metabolites that are produced have a positive coefficient. Since most reactions involve only a few metabolites, S is a sparse matrix. The size of S is m*n for a network with m metabolites and n reactions. The vector x with length m can then be defined as the concentrations of all the metabolites and the vector v with length n contains the fluxes through each reaction.</p> | ||
| + | <h5>Constraint-Based Models of E. coli[http://ecoliwiki.net/colipedia/index.php/Metabolic_Network_Reconstructions]</h5> | ||
| + | <h6>iAF1260</h6> | ||
| + | <p>The latest update of the E. coli genome-scale metabolic model is iAF1260, published in 2007. The total number of genes increased to 1260, along with increases to 2077 reactions and 1039 unique metabolites. The scope of the network was expanded, explicitly accounting for periplasmic reactions and metabolites. The model was reconciled with the lastest version of the EcoCyc database, and thermodynamic analysis was performed to predict the reversibility of reactions. As the latest version of the E. coli metabolic model, iAF1260 continues to be updated as new discoveries are made, and a new version will be released in 2010. iAF1260 and its predecessors have been used in studies of metabolic engineering, biological discovery, phenotypic behavior, network analysis, and bacterial evolution.</p> | ||
| + | <h6>E. coli core model</h6> | ||
| + | <p>The core E. coli model is a small-scale model of the central metabolism of E. coli. It is a modified subset of the iAF1260 model, and contains 134 genes, 95 reactions, and 72 metabolites. This model is used for educational purposes, since the results of most constraint-based calculations are easier to interpret on this smaller scale. It is also useful for testing new constraint-based analysis methods.</p> | ||
| + | <h3>Tools</h3> | ||
| + | <h4>openCobra Toolbox[http://opencobra.sourceforge.net/openCOBRA/Welcome.html]</h4> | ||
| + | <p>The COnstraints Based Reconstruction and Analysis (COBRA) approach to systems biology accepts the fact that we do not possess sufficiently detailed parameter data to precisely model, in the biophysical sense, an organism at the genome scale1.The COBRA approach focuses on employing physicochemical constraints to define the set of feasible states for a biological network in a given condition based on current knowledge. These constraints include compartmentalization, mass conservation, molecular crowding, and thermodynamic directionality.More recently, transcriptome data have been used to reduce the size of the set of computed feasible states. Although COBRA methods may not provide a unique solution, they provide a reduced set of solutions that may be used to guide biological hypothesis development. Given its initial success, COBRA has attracted attention from many investigators and has developed rapidly in recent years based on contributions from a growing number of laboratories – COBRA methods have been used in hundreds of studies.</p> | ||
| + | <h4>CellDesigner 4.0[http://www.celldesigner.org/]</h4> | ||
| + | <p>CellDesigner is a structured diagram editor for drawing gene-regulatory and biochemical networks. Networks are drawn based on the process diagram, with graphical notation system proposed by Kitano, and are stored using the Systems Biology Markup Language (SBML), a standard for representing models of biochemical and gene-regulatory networks. Networks are able to link with simulation and other analysis packages through Systems Biology Workbench (SBW).</p> | ||
| + | <h4>Others</h4> | ||
<h2>Week 5 (May 28 - June 1)</h2> | <h2>Week 5 (May 28 - June 1)</h2> | ||
Revision as of 16:15, 4 June 2012
Contents |
Week 1-3
Refer to Hydrocarbon Modelling Part [1]
Week 4 (May 22-25)
Concepts
Flux Balance Analysis (FBA)
Flux balance analysis (FBA) is a mathematical method for analyzing metabolism. It is a direct application of linear programming to biological systems that uses the stoichiometric coefficients for each reaction in the system as the set of constraints for the optimization.
The Steady State Assumption
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero. In chemistry, a steady state is a situation in which all state variables are constant in spite of ongoing processes that strive to change them.
Stoichiometric & Flux Matrix
Stoichiometry is a branch of chemistry that deals with the relative quantities of reactants and products in chemical reactions. In a balanced chemical reaction, the relations among quantities of reactants and products typically form a ratio of whole numbers.
Flux matrix, in terms of flux rate, is a rate of turnover of molecules through a reaction pathway.
Extended Flux Analysis
Flux variability analysis
The optimal solution to the flux-balance problem is rarely unique with many possible, and equally optimal, solutions existing. Flux variability analysis (FVA), built-in to virtually all current analysis software, returns the boundaries for the fluxes through each reaction that can, paired with the right combination of other fluxes, produce the optimal solution. Reactions which can support a low variability of fluxes through them are likely to be of a higher importance to an organism and FVA is a promising technique for the identification of reactions that are highly important.
Dynamic FBA
Dynamic FBA attempts to add the ability for models to change over time, thus in some ways avoiding the strict homoeostatic condition of pure FBA. Typically the technique involves running an FBA simulation, changing the model based on the outputs of that simulation, and rerunning the simulation. By repeating this process an element of feedback is achieved over time.
Metabolic Network Reconstruction
Metabolic network reconstructions are biochemically, genetically, and genomically (BiGG) structured knowledge bases that seek to formally represent the known metabolic activities of an organism. Network reconstructions also exist for other types of biological networks, including transcription/translation and signaling networks. Genome-scale metabolic networks have been reconstructed for nearly 40 organisms so far, including E. coli. These reconstructions are useful because they can be converted into constraint-based models, allowing useful predictive calculations like flux balance analysis to be performed. Constraint-based models of E. coli have existed for nearly twenty years. The first genome-scale model of E. coli metabolism was released in 2000, and this model continues to be expanded and updated today.[2]
Metabolic network reconstruction and simulation allows for an in depth insight into comprehending the molecular mechanisms of a particular organism, especially correlating the genome with molecular physiology (Francke, Siezen, and Teusink 2005). A reconstruction breaks down metabolic pathways into their respective reactions and enzymes, and analyzes them within the perspective of the entire network. </p>
Modelling
Constraint-based Model
Constraint-based models are a way of mathematically encoding a metabolic network reconstruction. Networks can be encoded as stoichiometric matrices (S), in which each row represents a unique metabolite and each column represents a biochemical reaction. The entries in each column of this matrix are the stoichiometric coefficients of the metabolites in the reaction. Metabolites that are consumed have a negative coefficient and metabolites that are produced have a positive coefficient. Since most reactions involve only a few metabolites, S is a sparse matrix. The size of S is m*n for a network with m metabolites and n reactions. The vector x with length m can then be defined as the concentrations of all the metabolites and the vector v with length n contains the fluxes through each reaction.
Constraint-Based Models of E. coli[3]
iAF1260
The latest update of the E. coli genome-scale metabolic model is iAF1260, published in 2007. The total number of genes increased to 1260, along with increases to 2077 reactions and 1039 unique metabolites. The scope of the network was expanded, explicitly accounting for periplasmic reactions and metabolites. The model was reconciled with the lastest version of the EcoCyc database, and thermodynamic analysis was performed to predict the reversibility of reactions. As the latest version of the E. coli metabolic model, iAF1260 continues to be updated as new discoveries are made, and a new version will be released in 2010. iAF1260 and its predecessors have been used in studies of metabolic engineering, biological discovery, phenotypic behavior, network analysis, and bacterial evolution.
E. coli core model
The core E. coli model is a small-scale model of the central metabolism of E. coli. It is a modified subset of the iAF1260 model, and contains 134 genes, 95 reactions, and 72 metabolites. This model is used for educational purposes, since the results of most constraint-based calculations are easier to interpret on this smaller scale. It is also useful for testing new constraint-based analysis methods.
Tools
openCobra Toolbox[4]
The COnstraints Based Reconstruction and Analysis (COBRA) approach to systems biology accepts the fact that we do not possess sufficiently detailed parameter data to precisely model, in the biophysical sense, an organism at the genome scale1.The COBRA approach focuses on employing physicochemical constraints to define the set of feasible states for a biological network in a given condition based on current knowledge. These constraints include compartmentalization, mass conservation, molecular crowding, and thermodynamic directionality.More recently, transcriptome data have been used to reduce the size of the set of computed feasible states. Although COBRA methods may not provide a unique solution, they provide a reduced set of solutions that may be used to guide biological hypothesis development. Given its initial success, COBRA has attracted attention from many investigators and has developed rapidly in recent years based on contributions from a growing number of laboratories – COBRA methods have been used in hundreds of studies.
CellDesigner 4.0[5]
CellDesigner is a structured diagram editor for drawing gene-regulatory and biochemical networks. Networks are drawn based on the process diagram, with graphical notation system proposed by Kitano, and are stored using the Systems Biology Markup Language (SBML), a standard for representing models of biochemical and gene-regulatory networks. Networks are able to link with simulation and other analysis packages through Systems Biology Workbench (SBW).
 "
"