Team:Calgary/Project/FRED/Modelling
From 2012.igem.org


Hello! iGEM Calgary's wiki functions best with Javascript enabled, especially for mobile devices. We recommend that you enable Javascript on your device for the best wiki-viewing experience. Thanks!
A Kinetic Model in MATLAB
The creation of our electrochemical sensor presented us with an interesting question: How fast will it be? Instead of trying many timecourses in the lab we turned to modelling to give us an answer. We have created a kinetic model for one of our systems, the uidA system, to give us an estimate of the time needed to observe a result.
How did we build it?
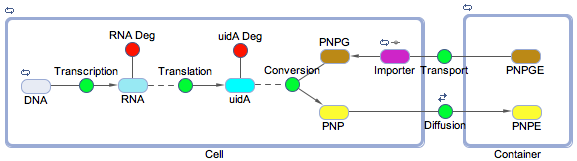
Using the SimBiology toolbox for MATLAB we created a framework of the electrochemical reporter system. We started at the genetic level, modelling transcription, translation, and the enzyme catalysis. We also included the transport of the substrate into the cell and the diffusion of the product out of the cell. The degradation reactions for the RNA transcript and the enzyme were also included. The reaction scheme is shown below in figure 1.
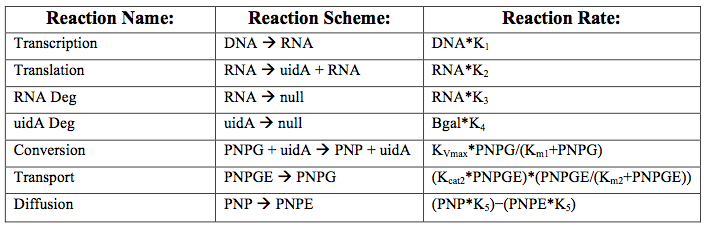
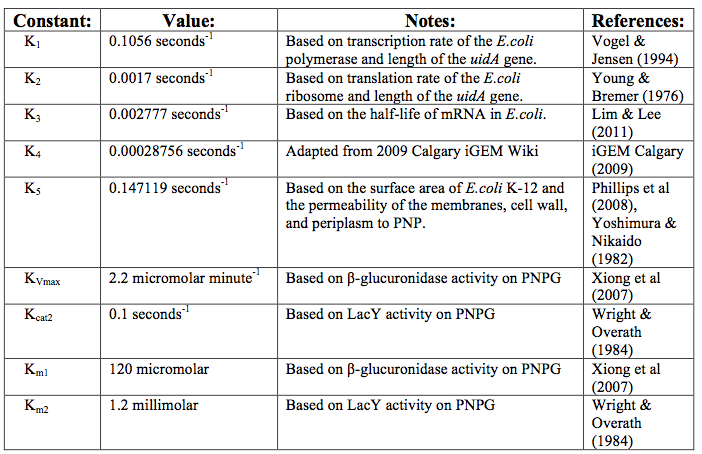
After creating the basic framework for the model we needed to create mathematical equations for each reaction with appropriate rate constants. These equations and the corresponding values are shown below in tables 1 and 2.
What did it show?
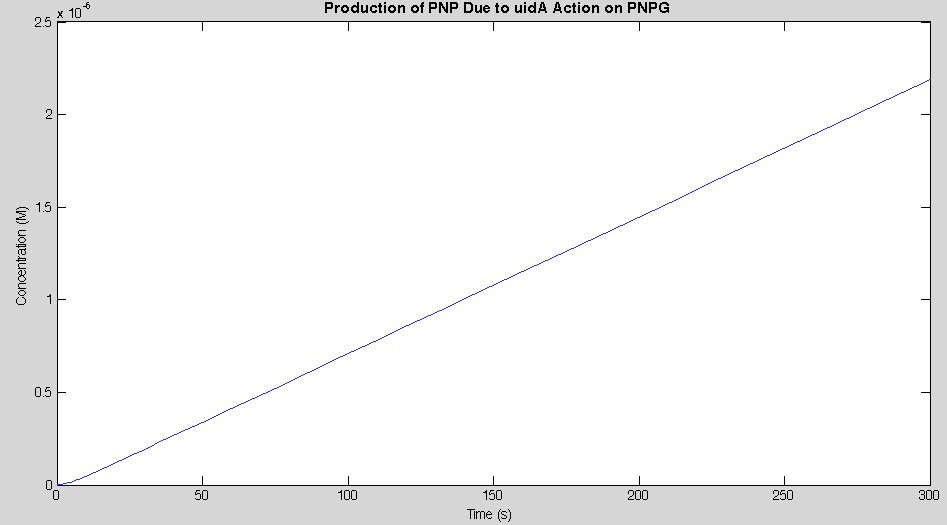
Before running the model we needed to decide what an appropriate endpoint would be. As we were trying to determine how quickly we could get a result we chose 2µM as our endpoint. This was chosen because initial electrochemical testing of PNP showed strong responses at concentrations as low as this. With our endpoint chosen the model was run and the data is shown below in figure 2.
Vogel U, Jensen KF. The RNA chain elongation rate in Escherichia coli depends on the growth rate. J Bacteriol. 1994 May;176(10):2807-13.
Young R, Bremer H. Polypeptide-chain-elongation rate in Escherichia coli B/r as a function of growth rate. Biochem J. 1976 Nov 15;160(2):185-94.
Lim HN, Lee Y, Hussein R. Fundamental relationship between operon organization and gene expression. Proc Natl Acad Sci U S A. 2011 Jun 28;108(26):10626-31.
2009 iGEM Calgary, 2009.igem.org/Team:Calgary/Notebook
Phillips R, Kondev J, Theriot J. Physical Biology of the Cell. 1st ed. Garland Science. 2008.
Yoshimura F, Nikaido H. Permeability of Pseudomonas aeruginosa outer membrane to hydrophilic solutes. J Bacteriol. 1982 Nov;152(2):636-42.
Xiong AS, Peng RH, Cheng ZM, Li Y, Liu JG, Zhuang J, Gao F, Xu F, Qiao YS, Zhang Z, Chen JM, Yao QH. Concurrent mutations in six amino acids in beta-glucuronidase improve its thermostability. Protein Eng Des Sel. 2007 Jul;20(7):319-25. Epub 2007 Jun 8.
Wright JK, Overath P. Purification of the lactose:H+ carrier of Escherichia coli and characterization of galactoside binding and transport. Eur J Biochem.1984 Feb 1;138(3):497-508.
 "
"