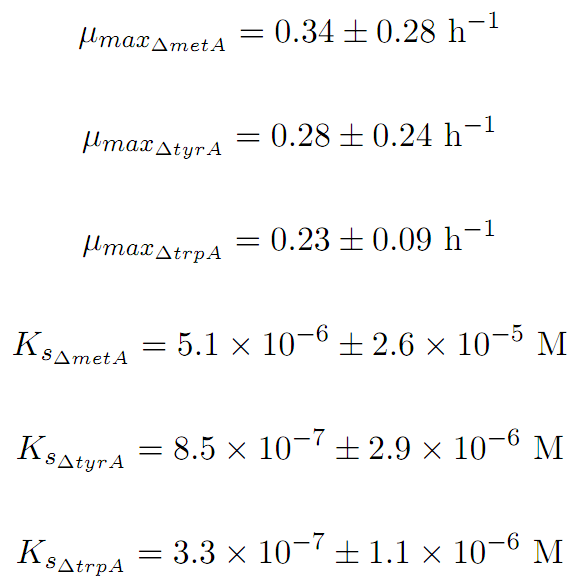Team:British Columbia/Consortia
From 2012.igem.org

Modelling Microbial Consortia: The Auxotroph Approach
To gain a predictive understanding of consortium dynamics in the wet lab, we chose to model a system of simple auxotrophic interdependence. This system also enables us to establish a rapid foundation for which to conduct preliminary model refinements.
The three interdependent E. coli auxotrophs studied in our project are ΔtrpA, ΔmetA, and ΔtyrA. These three strains are deficient in the production of the amino acids tryptophan, methionine, and tyrosine, respectively. Thus, in order for each strain to survive, they must exist in the context of a consortium. Our model is designed to predict the growth and survival of such a system, and is based on the measured amino acid excretion rates under basal genomic expression. The model is written such that it can be easily updated when specific tuning of the amino acid production rates is desired (for example, by introducing induction systems for amino acid production in trans), rendering it ideal for modelling tuned and un-tuned consortium dynamics.
The key assumption for this model is that the tryptophan, tethionine, and tyrosine are the only growth limiting substrates for the ΔtrpA, ΔmetA, and ΔtyrA E. coli knock outs respectively.
One important equation which has been incorporated into our model is the Monod equation. This equation is most commonly used to model for microbial growth and has been shown to fit a large variety of empirical data[1]. In addition, it shares the key assumption described above. This equation relates the specific growth rate (µg, the increase in cell mass per unit time) as function of the maximum growth rate (µm), and the concentration of a limiting substrate (S). The equation is written as follows:
Where KS is the limiting substrate concentration when the specific growth rate is at half maximum (KS = S when µg = µm/2). KS is also known as the saturation constant or half-velocity constant[1].
Equations:
Constants:
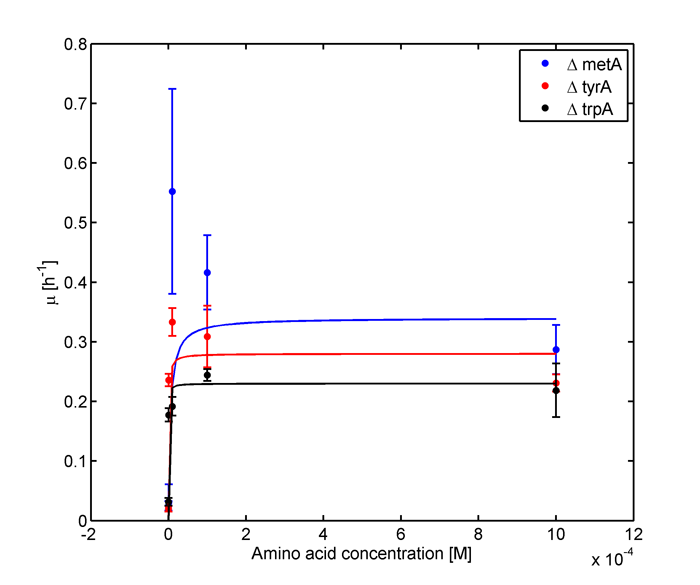
Some of the key constants for the Monod Kinetics are obtained through analyzing various growth rates under different known amino acid concentrations. The values are listed as follows:
and its wet lab data used is mainly based on the following graphs:
Figure 1: Monoculture Growth Rates at various Limiting Amino Acid Concentrations
Figure 2: Log Scale of Monoculture Growth Rates at various Limiting Amino Acid Concentrations
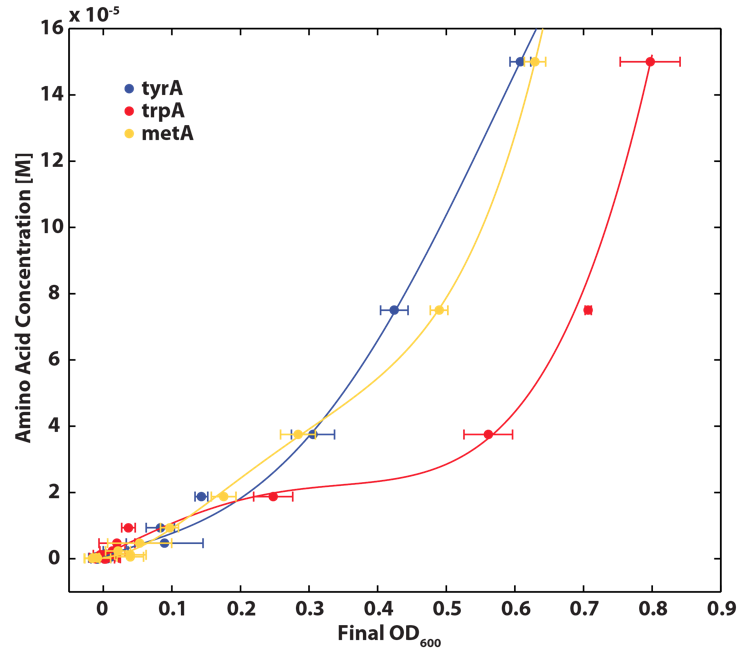
Also, we assumed that the amino acid consumption is solely depended on the cell growth and not the cell self maintenance. thus they are also obtained directly using our own wet lab data for these specific E. coli. We grew TrpA-, MetA-, and TryA- E. coli knock outs in 50 ml flasks with known initial Tryptophan, Methionine, and Tyrosine concentrations (5E-5 M) respectively, and harvested 5ml of cell free supernatants at various ODs. All these supernatants served as new 96-well plate media for each knock out cultures with newly added M9-Glucose shots (2% glucose in the well), which made sure the Amino Acid will be the limiting substrate for all knock outs. (Through previous experiments, we found that the each of the knockout monocultures will reach to a certain final OD, with respect to the media amino acid concentrations, thus we generated a calibration curve to relate the limiting amino acid concentration to their final OD readings.) These calibration curves are shown below:
Figure 3: trpA- Final OD and Trp Concentration Calibration Curve
Figure 4: metA- Final OD and Met Concentration Calibration Curve
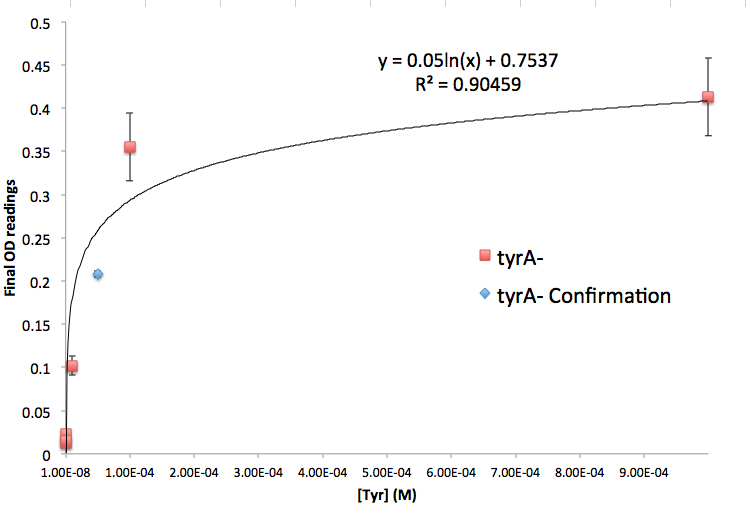
Figure 5: tyrA- Final OD and Tyr Concentration Calibration Curve
Note: We also tested the accuracy of one of the calibration curves. The blue dot in Figure 5 is another data value we obtained later at a known Tyrosine concentration (5E-5 M), and it is reasonably close to the predicted curve though not exactly the same. We are aware that this curve has limitation, mainly due to the big error bars at the higher OD data points, though this test point has proven that this calibration curve can serve us well at this stage of the research. Also, A Programmable Escherichia coli Consortium via Tunable Symbiosis also proved that this technique could be used for this purpose. (How should I say this, or should i say this at all??????????)
After growing the inoculated 96-well plate in humidified temperature control (37 deg) plate reader for 15 hours, their growth curves had been captured and most of the monocultures had reached their stationary phase, and the plate was then transferred to 37 deg room to obtain the remaining final OD readings.
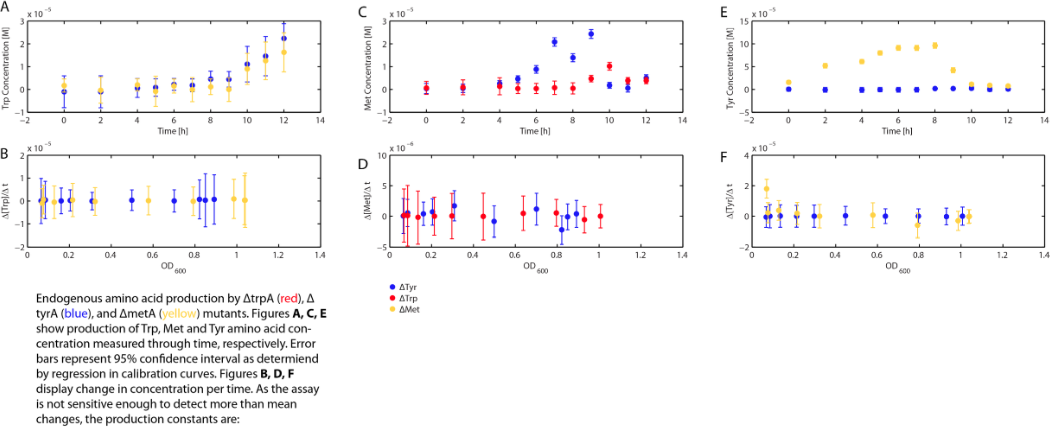
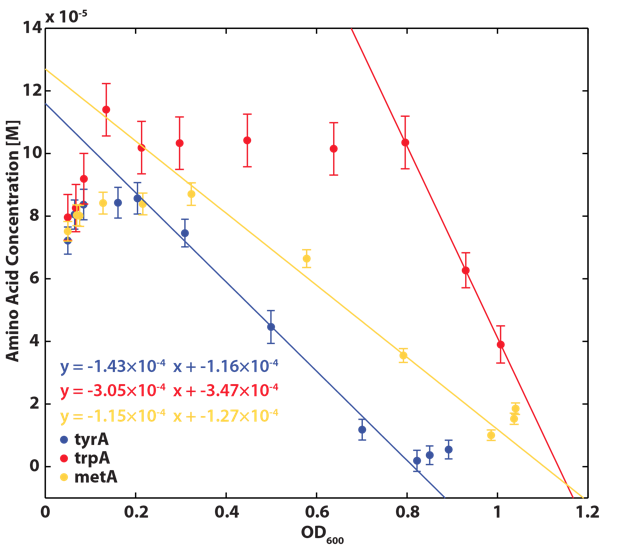
Based on the calibration curves above, the amino acid concentrations in the wells were calculated, and when corrected with a dilution factor of 5/4 (when we added in the M9-Glucose shot, it was 1/5 of the total well media volume), we arrived at the corresponding supernatant amino acid concentration at various monoculture OD readings. With the assumption that the only change in the amino acid concentration in the media is due to cell growths, and as they are specific knock outs, they were not able to produce any amino acid into the environment, each auxotrophs' consumption constant with respect to cell growth rate are calculated. Their values are:
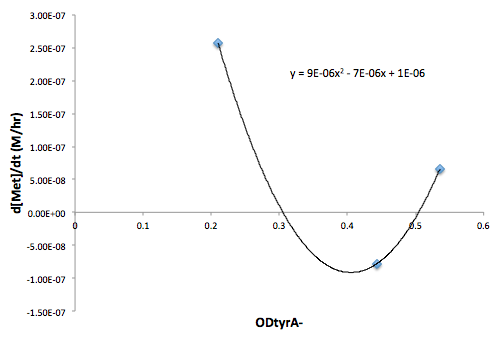
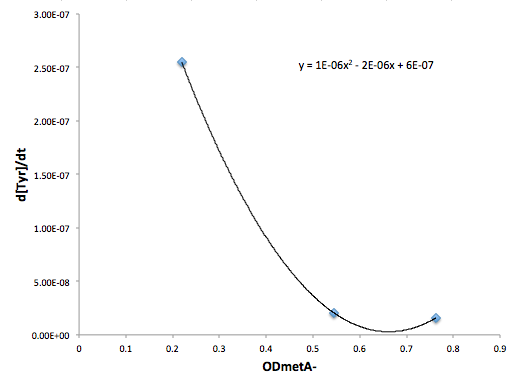
Moreover, in co-culture environment, to relate the contributions of the amino acid concentrations to the environment (media) of monocultures, the closest assumption we can make is that they will behave similarly to when they are in the monoculture conditions. Thus, we used the same method of relating the final OD to the limiting substrate amino acid concentration in the media, and found out the other two non-limiting amino acid concentrations of each knocked out E. coli auxotrophs (ΔtrpA, ΔmetA, and ΔtyrA) at various OD readings [2??]. With the consideration of sample taken time and some calculations, we were able to derive six functions that relate the change of all amino acid concentrations with respect to time (d[AA]/dt) with each auxotrophs' optical densities (ODaa), which is shown below:
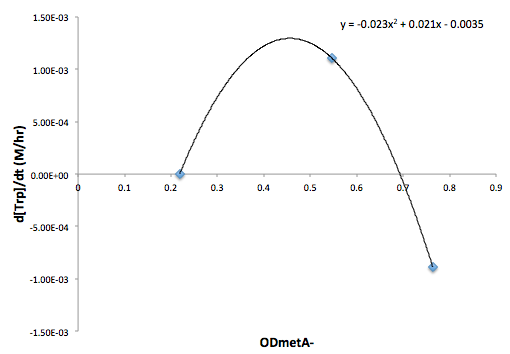
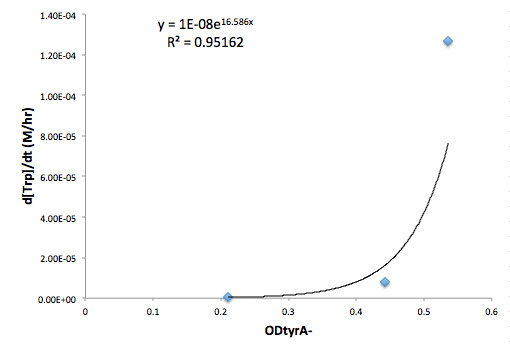
Figure 6: Change in Trp concentration as a function of metA- OD
Figure 7: Change in Trp concentration as a function of tyrA- OD
Figure 8: Change in Met concentration as a function of trpA- OD
Figure 9: Change in Met concentration as a function of tyrA- OD
Figure 10: Change in Tyr concentration as a function of trpA- OD
Figure 11: Change in Tyr concentration as a function of metA- OD
Based on these approximated functions, we were able to obtain the equations used in equations (1), (2), and (3).
.
Matlab Code
Now with all the key functions and constants defined, we are able to encode our model into Matlab, where the six key ODE functions can be solved and output our prediction of population dynamics
The code is shown below:
and when run the program, it predicts the population dynamics without inducing as shown in the following diagram:
As mentioned at the beginning, this code can be generalized to predict the population dynamics when there is a tuning effect, therefore we can use this model to see decide the amount of tuning we need to control the desired relative population of each auxotrophs.
References
[1] Shuler, ML; Kargi, F; Bioprocess Engineering Basic Concepts, 2002 2nd edition. Prentice Hall PTR.
[2] ????The Consortia Paper (this will be cited many places, and should be consistent in format.
 "
"