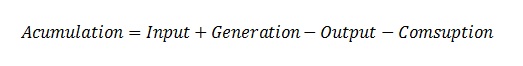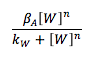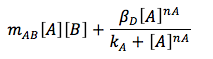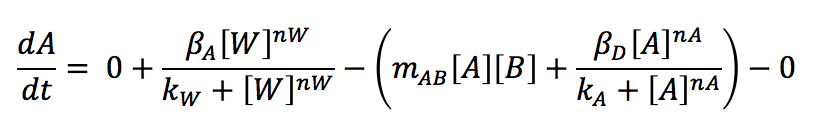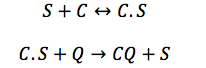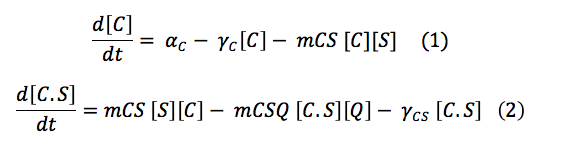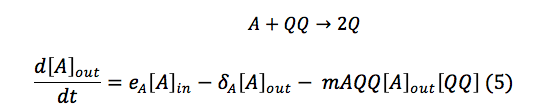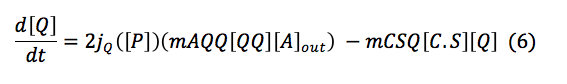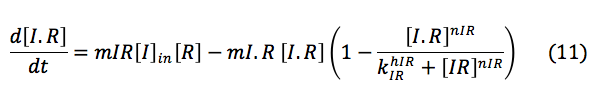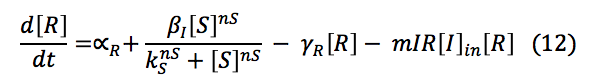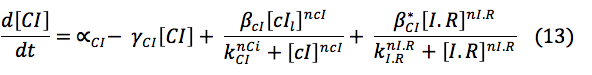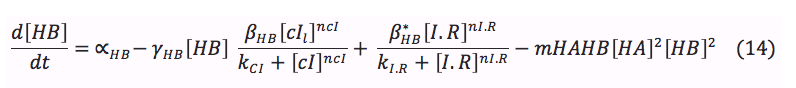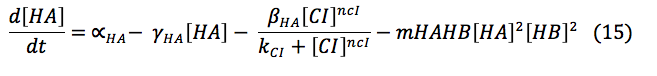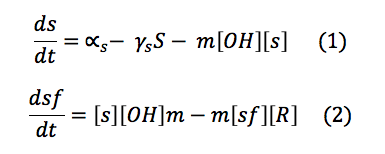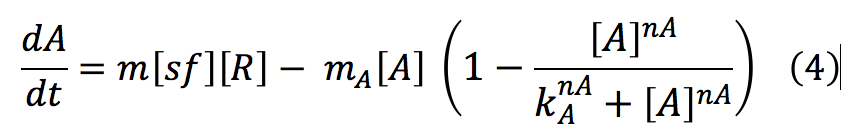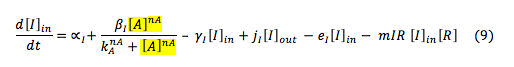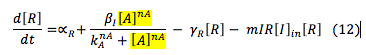Differential equations

Before experimentation with the designed bacteria and plants, we can check if this design works through a mathematical model of it. This model is based on the use of differential equations. This type of equations are deterministic because it describes the behavior for each of the substances in the synthetic circuit. However, they do not take into account the probabilities involved in each of the events described. Based on mass conservation:

In a biological system, the accumulation stands for the change in time, the input and output are related with the processes of exportation and importation of a molecule into the cell, the generation is related to the production by a gene or a chemical reaction, and the consumption is related to the chemical reaction too. All these terms depend on the reaction kinetics that could be a simple multiplication or a complex expression like a Hill equation.

Below it is shown an example to understand the previous ideas:

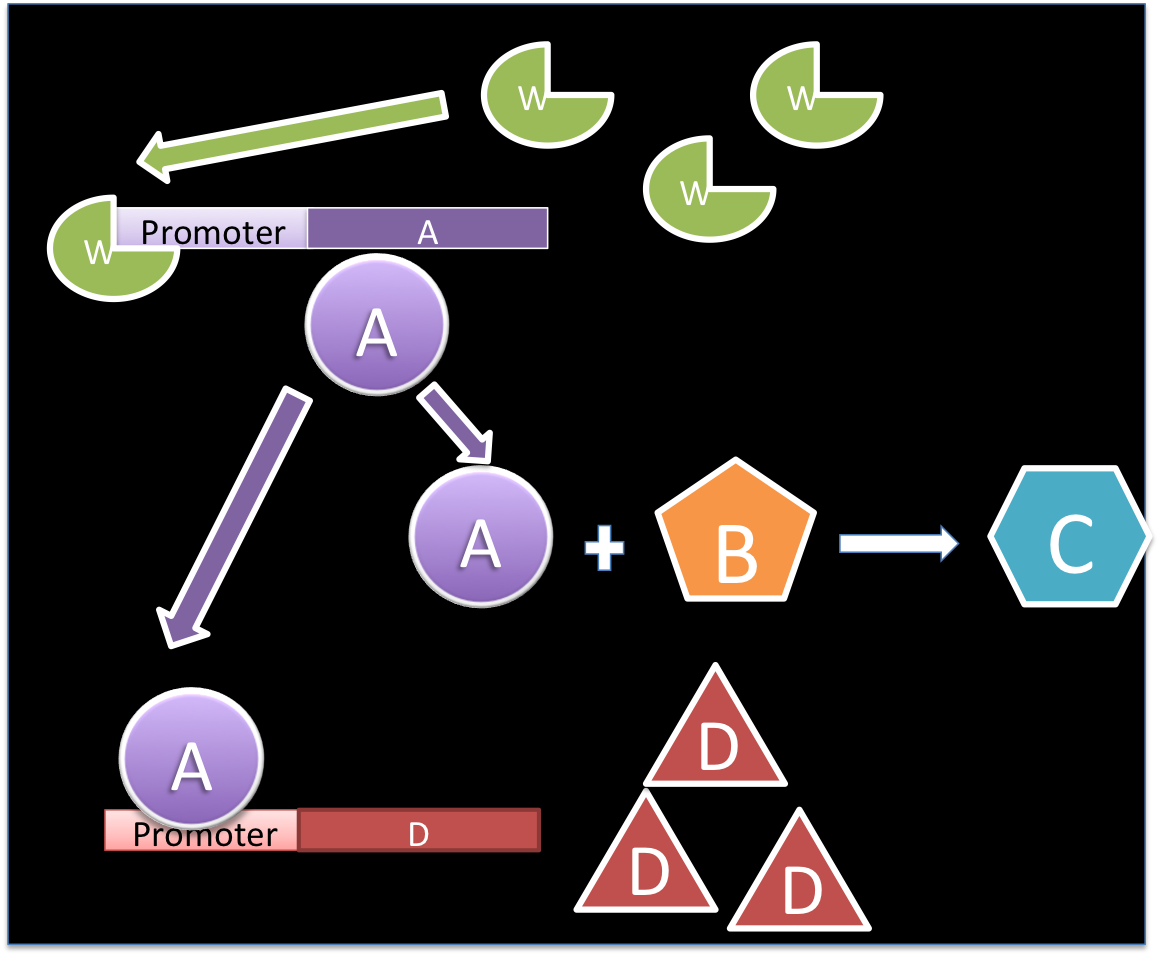
Example:

The molecule W promotes the production of A, which is used in a reaction with B for producing C and for the promotion of D.

Based on the mass balance for substance A, it is possible to see that there is not exportation or importation. Besides, there is not input or output term. The generation term is the production by the gene promoted by W, and it can be expressed with a Hill kinetic:

The consumption term is divided in two: first the reaction with B, that can be expressed as a first order reaction with a kinetic constant m and the promotion of the protein D that has a Hill kinetic:

Writing the complete mass balance equation for substance A:

This procedure was made for each of substances in the designed circuit. As shown above, Hill equations were used. Once all parameters in Hill equation are known, these can be solved using a specialized software like Matlab. This software allows us to solve the differential equations with a Runge - Kutta algorithm or using one of its tools like ODE45.

Differential equations for Pest-busters

RUST

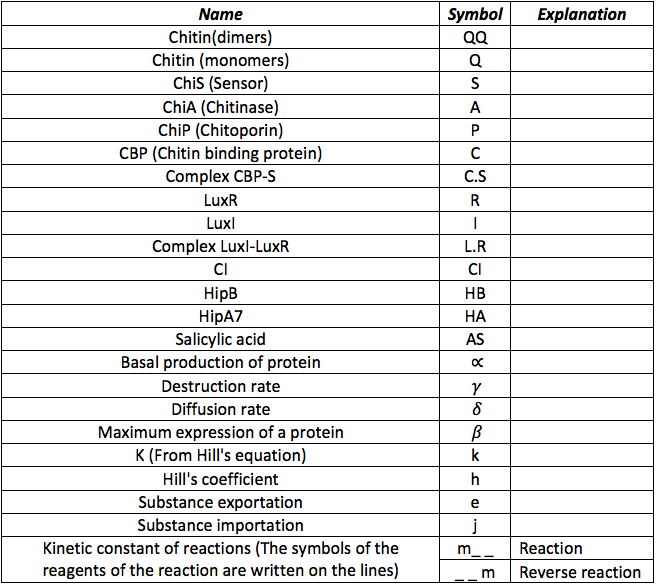
Below it is shown how differential equations for Pest-busters were made. However, before describing the equations it is necessary to know all the symbols that will be use in the documents and the simulation. The following table contains all the substances involved in the processes and the constants required for the simulation.

CBP: The Chitin binding protein participates in two major processes. First, it binds to the sensor. Second, when the chitin is in the cell, the CBP binds to it.

This set of equations involves de change of CBS free in the cell and the change of the complex C.S. With the production, the destruction rate and the reactions describe above the equations are:

ChiP: The chitioporin is the one that allows the entrance of the chitin monomers into the cell. Its production is regulated by the sensor (S), this regulation is expressed as a hill equation. The differential expression also includes the basal production and the rate of destruction; it is assumed that all the chitoporin produced goes to the membrane.

ChiA : chitinase The chitinase inside the cell depends of its basal production and the induction made by the sensor protein (S). The exportation of this enzyme is also involved in the equation.

The chitinase outside the cell depends of the rate of exportation of the chitinase inside, the diffusion in the environment and the reaction with the dimers of chitin.

Chitin: This equation measures the monomers of chitin inside the cell. This depends of a function of importation that depends on the quantity of chitoporins and the creation of chitin monomers outside the cell. This monomer is consumed in the reaction made with the complex C.S.

Sensor: This protein is one of the most important in the detection system, its function is to activate the promoters of P,A and I. Once the chitin enters to the cell S frees from the complex C.S and starts activating promoters.

This protein has two equations, the first one is and expression that shows the total of S in the cell. And the last one describes de total of the S protein free in the cell.

The second one shows the terms involved in the formation of the complex C.S and the liberation of S after the chitin enters into the cell. It also includes terms associated to the binding of the S protein with promoters regions and its reverse reaction, the unbinding of the promoter site. This expression wasn't taken into account, because its change it insignificant compared with the all system.

LuxI: The I protein that is inside the cell depends on the basal production and normal degradation rate, also of its promotion by the S protein, the exportation and importation from the cell and its reaction to make the complex with R

The I protein outside the cell only depends on the rates of exportation and importation from the cells and the diffusion into the environment.

The complex I.R activates one of the promoters of CI and HB and its creation depends of the concentration of I and R .

LuxR: The R protein is only involved in the creation of the complex L.R.

CI and HipB: The same promoters produce these two proteins downstream. Its creation depends on the activation of the promoters, the basal production and rate of destruction. Even though the CI promoter has three boxes it was found in the literature a paper where it can be modeled as a simple box and the parameter are already known .

HipA7 and Salicylic acid: These two proteins are activated by CI. Its concentration on the cell depend of the basal production, the rate of production when it is activated and the rate of destruction. Additionally the Salicylic acid is exported outside the cell for the plant signaling, and the toxin HA reacts with the antitoxin to awake the cell.

---

RALSTONIA

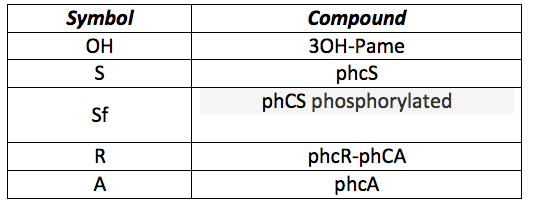
In this model the only thing that changes is the detection system. Now we want to sense 3-OH-PAME instead of Chitin. All the system involving CBP, chitinase and chitoporin is replaced with the sensor pchS and the transcription activator pchA, so the differences in the differential equations are in the first part only. The following table presents all the new substances involved in the process:

phcS: This molecule is the sensor of the OH. When the OH is in the environment the sensor is phosphorylated and phosphorylates the phcR-phcA complex. This set of equations includes the basal production and normal degradation of the sensor and the phosphorylation processes.

phcR: This complex is normally in the cell with a rate of basal production and destruction. It is broken when the Sf phosphorylates it and the phcA is freed.

phcA: This protein is the activator, it is freed after the phosphorylation of R and it binds to a promoter, in this case the CI and HipB promoter.

The equations of the second part are the same as in the rust model (Equations 9-16), the only difference is that the promoter of the LuxI-LuxR system is now induced by A: