"

From 2012.igem.org

Team Colombia @ 2012 iGEM

Template:Https://2012.igem.org/User:Tabima

Parameters of the equations

When we want to model a biological process, it is necessary to write the differential equation that model the system which requires a number of constants. If the real value for the constants are unknown, the system can not have any biological sense. These entries are called parameters and they are crucial elements in the mathematical model made in this project.

There are three possible ways to find this parameters:

i) Literature. There are a lot of studies trying to find biological parameters, such as basal rate of protein production, kinetic constants, Monod's constants, etc. Moreover, there are so many biological systems and only a few of them have been characterized. Thus, it is difficult to find the parameters that are needed.

ii) Experimental way. If an experiment is made using the biological system of interest, it is possible to find the parameters for the equations that models the whole system. For this project, it was necessary to model the biological system first. Thus, experiments couldn't be performed to find the constant for the differential equations.

iii) Screening of parameters. Sometimes we don't have the exact number that we need, but we have a rank where it could be or the parameter for a similar biological system, then we can perfom a screening of parameter, where we try to find the value that perfectly fits the reponse of our circuit.

How did we do it?

For our biological system we use options i) and iii). In the literature it was possible to find the parameters for the complete CI activation box and for the rest of values we found an aproximately rank where they could be, so we proceeded to step iii).

We used a lot of resources and methods to approximate the limits for this ranges here is its explanation:

a.Basal levels of the proteins:

To determine a range in which this value we described mathematically a very simple process. Suppose there is this typical differential equation:

Where αo is the basal level, γ is the protein parameter for degradation and P is the protein concentration, now with this, we can assume that in steady state conditions we have that dP/dt= 0, then:

But γ is approximately 1/T, having that:

To establish the range we assumed T as φ and we looked for a normal range of concentration of a protein in a cell [http://bionumbers.hms.harvard.edu/bionumber.aspx?&id=104520&ver=10&trm=protein]. Another important aspect we took into account is that there were constitutive's proteins and inducible's proteins, so we divided the basal levels in two class, one for the basal proteins and other for the constitutive proteins, now with this, the following ranges were defined:

Basal proteins range (LuxR, LuxI, HipB and Salicylic Acid):

Constitutive proteins range (HipA7,Sensor, Chitinase, Chitoporin and CBP):

By other part the basal production of HipA has to be constitutive and inducible because we want the cell to be always sleep (constitutive) and when there is an impulse of chitin or 3-OH-PAME that awakes the cell, we want a positive control to make it sleep again (inducible). The basal concentration used in the equations was the constitutive one because is the number that's gonna have more effect in the response.

b.Protein degradation:

Our unit of time is the bacteria's life's time, because in normal cells it's when the proteins are diluted and become less in the cell. One of the facilities of using for the values related with time the E.Coli’s lifetime is that we can establish easily the protein degradation, taking in count that a determined amount of proteins is always destructed each time our unit time is completed, we defined the protein degradation for almost all values as follows:

Again we can found that there is a special case, the degradation of HB is greater so we assigned it a value of 4/φ.

c. Reaction constant:

This value can vary a lot depending of the process we are describing, fortunately we found an article that describes how to approximate this value [http://www.biokin.com/dynafit/scripting/html/node23.html#SECTION00431000000000000000] so we took the given approximation and turned it into our units establishing a range we considered prudent.

d. Hill coefficients k:

First of all, we looked for some reference in different data sources where we found the coefficient of CI ([http://www.sciencemag.org/content/307/5717/1962.short Nitzal et al.2005]), now with this, we decided to approximate a range taking this value as a reference.

e. Hill coefficients n:

This case was similar to determining the hill coefficient k, we based on the value of n found for CI( [http://www.sciencemag.org/content/307/5717/1962.short NItzal et al.2005]), it’s important to say that in this case there was not necessary an analysis of which where the units to use.

Maximum cell concentration (β):

Having that the concentration of Rubisco, which is about 20 times the average concentration of a protein [http://bionumbers.hms.harvard.edu/bionumber.aspx?&id=107431&ver=1&trm=rubisco], and the rate of a producing a average protein we assign the limits for this range.

Once the ranks of the parameters were set, we proceed to do the screening. We tried a lot of techniques and most of the failed, here we present the steps of the succesful one:

1.Sensitivity Analysis

Now we have an idea of which parameters affect the response the most. Although we still don't know what is the exact value of the parameter we know how the system is supose to response.With this two things we can proceed to step 2.

2. Optimization of parameters

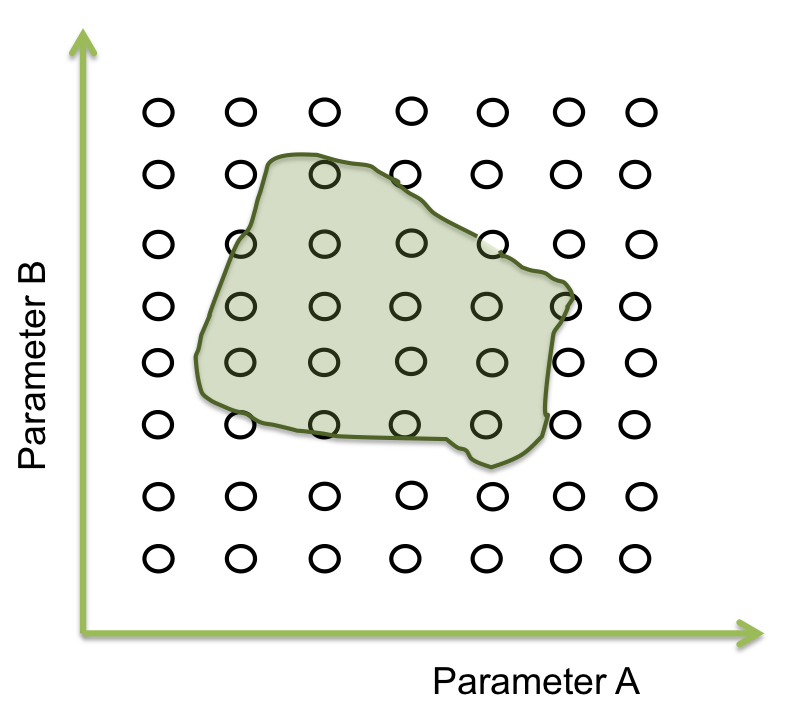
Within all the ranges of the parameters there is a number that combined with the other parameters makes the system behave just like is expected. There are many possible combinations where this can happen, and is represented as an area where the system woks. The figure below shows an example of the acceptable area of two parameters.

In two dimensions this sees easy to identify but when we are dealing with more than 10 parameters, doing this by hand or with iterations in a computer takes a lot of time (weeks or even months).

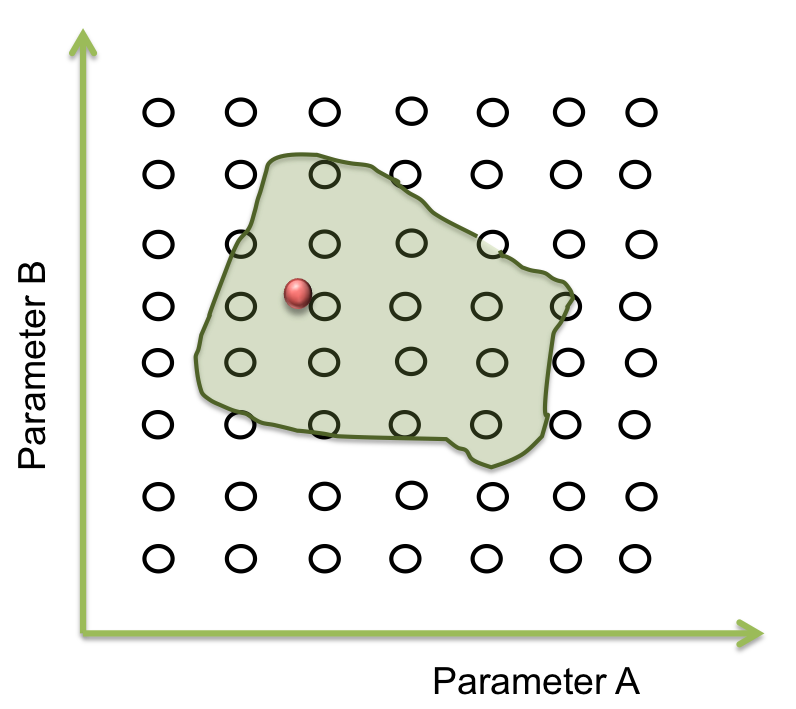
The goal in this step is to find a point within this area and from here the screening can begin. And one way for doing this is by a process of optimization

A process of optimization takes a function and maximizes o minimizes changing some variable of it. The changing variables are named optimization variables and function is called objective function. If we want to have some limitations or behaves with the variable we can add restrictions to the system, and the function will be optimized without breaking this limitations.

In our case the objective function is a minimum difference of squares between the points of our expected behavior and the response of the equations with a set of optimization variable. When the distance between these points is minimum the parameters are found!!!

This optimization process was done discretizing the differential equations and putting them as restrictions, the same was done for the stable state concentration where the differential equation must be equal to zero when the chitin is zero. All was programed in the software Gamside.

Unfortunately the firsts results were not satisfactory, so we are now developing a new code to run.

3.Screening

If we have a set of parameters why do we do a screening?

In the last step we found a set of parameters that give the expected response of the system. But this is only a point... What does happen with the rest of points of the area? Does the optimization method “know” if these parameters are real or have biological sense? As long as we specified one single response for the parameters, we don’t know if there are other possible responses of valid solutions. Do they exist?

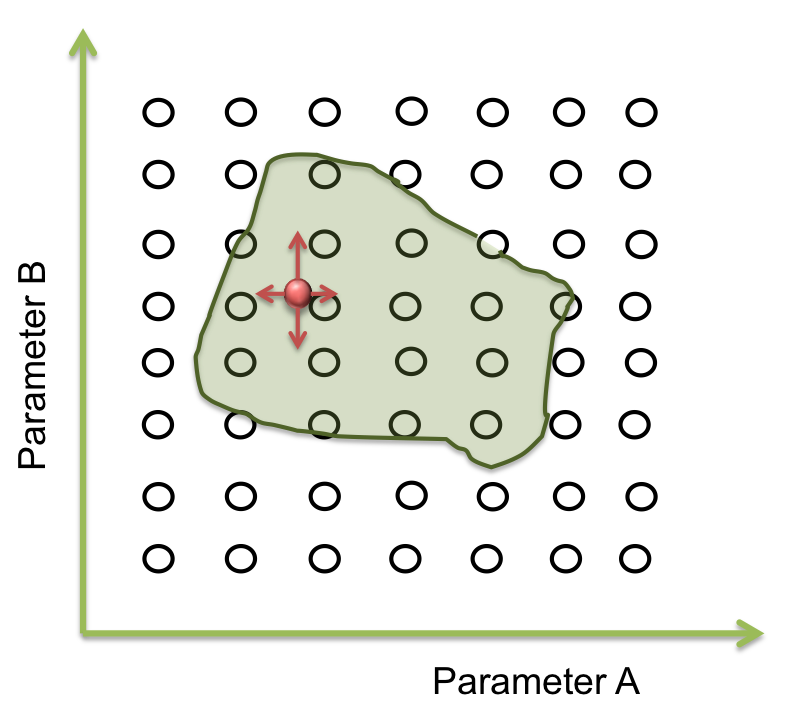
To answer these questions we performed a screening of the parameters. Beginning at the resulting point of the optimization, we started to move in all directions in a fixed range and then we examined when the acceptable area ends.

How much do we move, depends on the sensitivity analysis – If the response is not very sensible to the parameter, we take longer steps than the case in which the response is largely sensible.