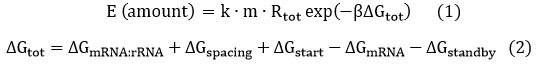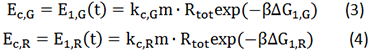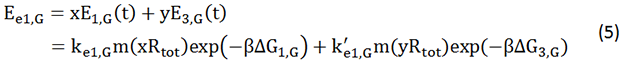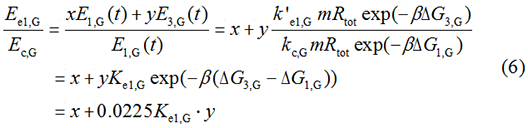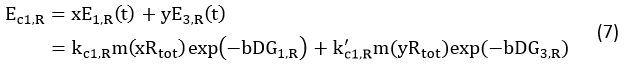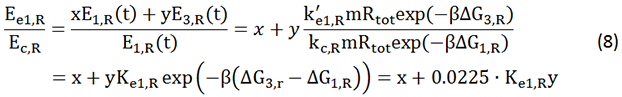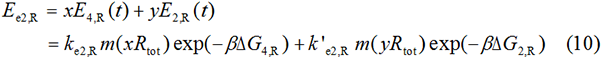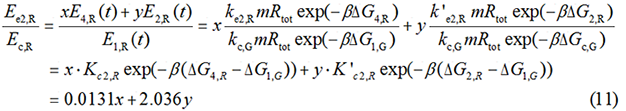Team:Tianjin/Modeling/Calculation
From 2012.igem.org

Contents |
Overview
Three problems came up while we start calculating: what sequences to input, which method to use and how cogent the result will be. As for sequence, we input the both the SD and the protein coding sequence.
Our goal is to calculate the total ΔG of each reaction and then predict the amount of protein expressed. There are several softwares dealing with DNA or RNA base-pairing progress, such as NUPACK, RBS-Calculator, and Vienna RNA etc. After comparison, we decide to use RBS-Calculator.
Due to the complication of translation progress and our lack of insight in this issue, the results of our modeling can’t be very precise. But at least it should have the precision of order of magnitude.
Input of Our Calculation
RBS sequence
- RFP, normal RBS
ATTTCACACATACTAGAGAAAGAGGAGAAATACTAGATGGCTTCCTCCGAAGACGTTATCAAAGAGTT
CATGCGTT
- RFP, orthogonal RBS
ATTTCACACATGTTCCGTACTAGATGGCTTCCTCCGAAGACGTTATCAAAGAGTTCATGCGTT
- GFP, normal RBS
TACTAGAGAAAGAGGAGAAATACTAGATGCGTAAAGGAGAAGAACTTTTCACTGGAGTTGTCCCAAT
TCTTGTT
16S rRNA sequence
- normal 16S: ACCTCCTTA
- orthogonal 16S: ACGGAACTA
Formula Derivation
Basic Idea
For model design, please refer to Design part. Data of the curve Er-time is obtained from Ec=K∙Er experiments. The function of our model is to work out the proportion factor 'K'.
Basic Assumption
- The expression of RFP and GFP are independent.
- The expression of the two proteins are determined by the percentage of normal and orthogonal ribosomes rather than the number of the two ribosomes.
- The growth curve of bacteria do not change significantly after the transferred into orthogonal protein expression system.
Formula Derivation
We start from Formula 1 and 2. In Formula 1, m stands for the number of mRNA transcript, Rtot is the total number of ribosomes, β is the apparent Boltzmann constant, ∆Gtot is the total change of Gibbs free energy, k is proportion factor.
Because the GFP and RFP coding sequence are on the same mRNA transcript, the values of m of GFP and RFP are always same. In different state and time, the total number of ribosomes varies. We assume that at the same time Rtot of different state remain same. Calculation of DGtot is the main job of this model. The proportion factor 'k' represents all unknown factors. Here we assume that as for the same protein in deferent state 'k' varies little.
The Calculation
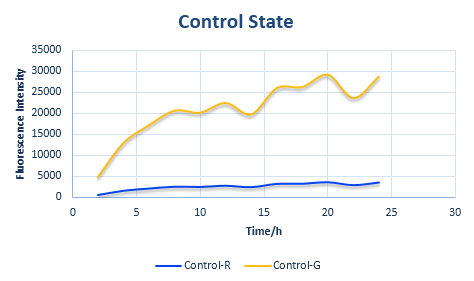
Control State (c)
The two formulas above serve as denominators in following deduction. We get series of disjointed data of function 3 and 4 through experiments. The amount of GFP and RFP can’t be measured directly so we measured the fluorescence intensity of each protein. And because all the formula in this model are based on a singular cell, we must consider the influence caused by the number and growing condition of bacteria.
Experimental state 1 (E1)
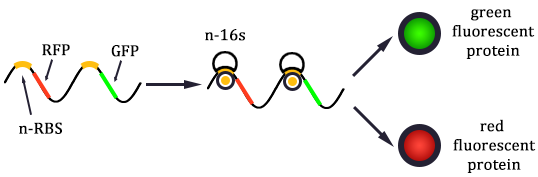
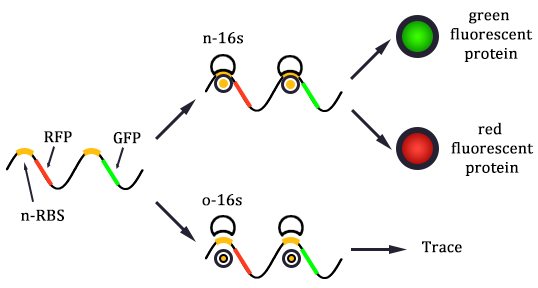
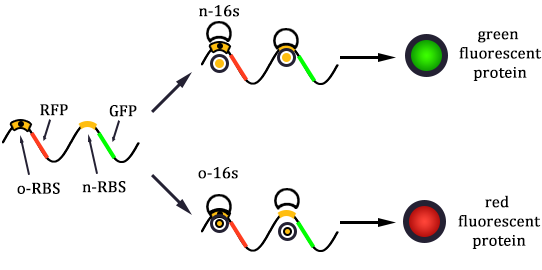
The expression of GFP is composed of two part, the expression of n-RBS::n-16S and of n-RBS::o-16S.
There is no difference for the expression of GFP in Experimental state ONE from the control state, except for the distribution of ribosomes. For this reason, we presume that kc1,G and kr,G are nearly equal and thus Kc1,G equal to 1. The same thought is also shown in following derivation.
We noticed that the proportion factors in equation 6 and 8 are equal, which is not a coincident. This is because ΔG3,G-ΔG1,G≈ΔG3,R-ΔG1,R. The difference of ΔG3,G and ΔG1,G.
Experimental state 2 (E2)
Note : Strictly speaking, the factor K should better be obtained from experimental data rather than assumed to be 1 for such simplification could lead to much deviation from real value.
The Calculation of ΔGtot
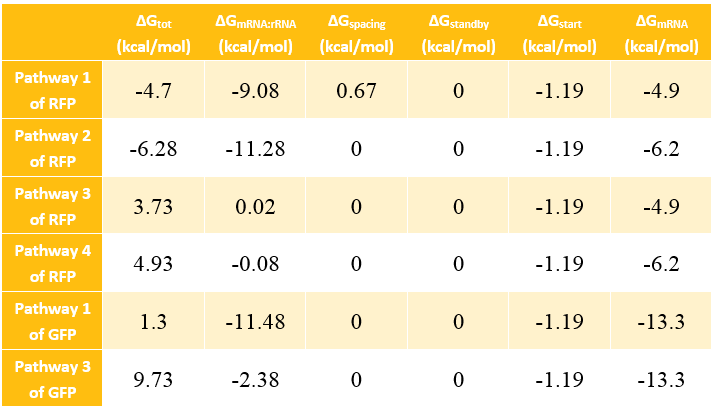
In most cases, the difference of delta G among the four pathways are mainly reflected by the ΔGmRNA-rRNA. There are two ways to calculate the ΔGmRNA-rRNA:
- With the help of RBS calculator;
- Use the method in literature Computational design of orthogonal ribosomes.
There are some differences between the input and output of the two method.
1st method:
- input:
- standby + RBS + Spacing + Start Codon + Protein-Coding,
- 16S 3' last nine bases;
- output: ΔGmRNA:rRNA, ΔGstart, ΔGspacing, ΔGstandby, ΔGmRNA;
- Software: RBS-Calculator;
- Strength: taking more factors into our consideration and are more accessible to real condition;
- Weakness: not sure of the input sequence.
2nd method:
- input:
- ASD sequence,
- SD sequence (each are 6 bases long);
- Output: ΔG under different conditions;
- Software: RNA-Cofold in Vienna RNA web servers;
- Strength: only need to input the SD and ASD sequence which is very easy;
- Weakness: not as accurate as the first method.
Similarity of the two method:The core program of RBS-Calculator is based on Vienna RNA.
There are also two points that should be focused on during our modeling:
- the specification of input;
- the analysis of errors if there are any in the output.
As for analysis of errors, the most frequent errors are the Long-Range Paring which occurred when the head and the tile of the mRNA sequence complement with each other within the sequence itself. In such case, the ΔGmRNA result is not accurate. We usually use RNA-Fold to calculate the accurate ΔGmRNA to avoid such error.
Calculation Results of ΔG
Prediction of Protein Expression Amount
We should, first of all, measure the relative protein expression amount (fluorescence intensity) and to obtain the parameters in the model through regression. After the obtaining the model parameters, we can predict the amount of protein expressed and to compare them with that of wet lab results. The workflow of our prediction process is shown in Figure 4.
Model Extension
In the previous protein expression model, we just suppose the existence of the orthogonal expression system do not have any significant impact on our system. However, to make our system more accurate, we also need to take the factor of estimation.
 "
"