Team:Amsterdam/achievements/stochastic model
From 2012.igem.org




Here we will propose a solution to the the background noise observed in the experiments, and conclude what rates of leakiness are acceptable to the system. In this, we model the system both using both ordinary differential equations and stochastically using the Gillespie SSA algorithm.
We will focus on the effects of two rate constants in particular on the fraction of methylated plasmids in absence of the inducing signal:
- the leaky transcription rate of the mRNA for the fusion protein (FP), denoted by $k_{c\text{MFP}}$
- the catalysis rate of the FP, or the rate with which it methylates umethylated plasmids
Contents |
Leaky expression rate
There are discrepancies between the definitions used in the literature on what leaky expression exactly is:
- The most favoured definition seems to be the that leaky operons show low expression rates even when bound by a negative transcriptional regulator (REF). In this perspective the transcriptional regulator is regarded to be unable to completely silence gene expression. In this case the only way to get a value for leaky expression is to measure it experimentally. In this process, care should be taken to be specific about what version of the operon exactly is being used. Some repressors are known to regulate transcription by binding to DNA regions that are very distant from the controlled operon. 'Plasmid versions' of these operons might not contain these distantly located binding sites and are therefore less likely to be optimally repressed.
- Another definition is that the TF can fully silence gene expression and that leaky expression is caused by seldomly occurring dissociation events between between the TF and the DNA operator sequence.
During these short time windows of opportunity, the RNA polymerases would then be able to quickly transcribe a small amount of RNA. Multiplying the maximal rate of transcription by the time fraction during which the polymerase is able to bind gives an indication of the leaky transcription rate defined this way.
The following relationship must always be true: $[O_{\text{Total}}] = [O_{\text{Free}}] + [R_{2}O]$ with $R_{2}O$, the operon bound by a dimerized repressor, computable from $\frac{[R_{2}][O]}{K_{d}}$. Solving for $O_\text{Free}$:
$$ \begin{align}
[O_{\text{Free}}] = O_{\text{Total}} - O_{\text{Free}} = O_{\text{Total}} - \frac{[\text{O}][\text{R}_{2}]}{[\text{OR}] = \text{O}_{\text{Total}} (1 + \frac{[R_{2}]}{K_{d}})}
\end{align} $$
We immediately see that the $[O_{\text{Free}}]$ depends on $[R_{2}]$ and $O_{\text{Total}}$. The dissociation constant of the dimerized LacI-repressor for its operator sequence has been determined to be $10^{-12} M $ and the volume of E. coli is $0.7 \mu m^{3}$. The transcription rate in E.coli is 40-80 bp/s. <finish this calculation>
The leaky expression rate can also be extracted from this website, which states that expression is reduced 1000-fold with bound repressor.
Fusion protein catalysis rate
The catalysis rate $k_{cat}$ has not been determined for the MTase that we are using, M.ScaI. However, for another MTase with the same [http://www.brenda-enzymes.info/php/result_flat.php4?ecno=2.1.1.113 EC2.1.1.113 number] as M.ScaI, BamH1, the $k_{cat}$ has been determined to be $0.0175$ (Cheng1999).
Cell growth rate
Experimental measurements of the growth rate of bacterial strain <math>DH5\alpha</math> transformed with two of our preliminary constructs showed that their growth rates (<math>\mu</math>) were around <math>80 min^{-1}</math> ([/Team:Amsterdam/Project/Growthcurves Experimental growth curves]). In these simulations, cellular division was therefore assumed to be Gaussian distributed with $\mu = 80$ and $\sigma = 2$.
Leakiness and background noise
This model has as its main goal to identify how much the uninduced operon expression rate and the catalysis rate of the FP affect the methylation status of the plasmids. Each plasmid is assumed to have one bit and one operon that includes the fusion protein. Running the stochastic version of this model, we noticed that keeping the amount of equations to a minimum is paramount to success, as the computation time seems to increase exponentially with the amount of reactions in the system. Focussing on the leakiness rate instead of the repressor-operon interactions that would require a lot of equations, we will therefore make one bold assumption: all operons present in a single cell are permanently bound to a transcriptional repressor. This frees us from having to code the signal entering the cell and binding the repressing TF, granting focus to the leaky expression rate and the catalysis rate of the fusion protein. For these models to have any forecastable value therefore, the amount of repressor molecules present in the system has to be much greater than the amount required to cover all operons.
In order to not exclude the possible qualitative difference in model behaviour when all molecular reactions are computed individually, the system has also been modelled stochastically. To make the two systems perfectly comparable, the used rates are qualitatively identical to the ones used in the ODE system. Furthermore, the same parameter values have been used.
<conclusions> Different behaviour?
ODE Model definition
mRNA for the FP results only from leaky expression and is degraded: $$ \frac{mFP}{dt} = k_{\text{sMFP}} \cdot \text{O} - \lambda{l}_{\text{MFP}} \cdot \text{MFP} $$ FP is created from mRNA and degraded: $$ \frac{FP}{dt} = k_{\text{sFP}} \cdot \text{MFP} - \lambda{l}_{\text{FP}} \cdot \text{FP} $$ Unmethylated plasmids are created from both unmethylated and methylated plasmids; methylation is not transferred to daughter plasmid during plasmid replication in prokaryotes. Plasmid growth continues until the plasmid copy number $Ca$ has been reached: $$ \frac{\text{PlasU}}{dt} = k_{\text{Plas}} (1 - \frac{(\text{PlasU} + \text{PlasM})}{Ca}) - k_{cFP} \cdot \text{FP} \cdot \text{PlasU} - \lambda_{\text{Plas}} \cdot \text{PlasU}, $$ Methylated plasmids result from the fusion protein finding an umethylated plasmid and methylating it: $$ \frac{\text{PlasM}}{dt} = k_{c\text{FP}} \cdot \text{FP} \cdot \text{PlasU} - \lambda_{\text{PlasM}} \cdot \text{PlasM} $$ The amount of (repressed) operons is identical to the amount of plasmids currently in the system: $$ \text{O} = \text{PlasU} + \text{PlasM} $$
| Parameter | Value |
|---|---|
| Ca | $200\ \text{or}\ 40$ |
| ksFP | $30$ |
| lMFP | $0.462$ |
| lFP | $0.2$ |
| kPlas | $0.00866434 \cdot Ca$ |
| lPlas | $0.00866434$ |
| Parameter values used to plot the ODE-system |
|
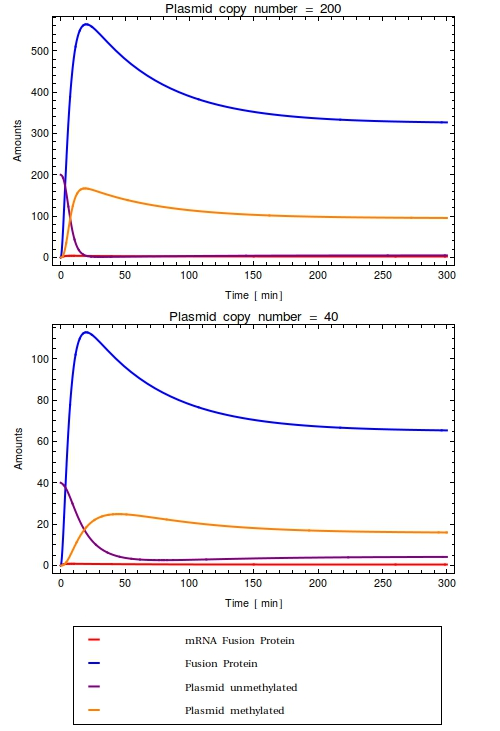
Looking at the plots for both the high and the low copy number plasmids, no qualitative difference is observable. All species in the system simply reach a steady state defined as the fraction between their production and degradation rates. Most notably, in the steady state that this system reaches all plasmids are methylated. This is very undesirable of course!
Steady state parameter scanning
In order to deduce what ranges of operon leaky expression and FP catalysis rates would yield acceptable leaky expression, a steady state parameter scan has been performed.
Our experimental results can thus be explained by any combination of the two parameters which which has an intermediate value in plot.
Stochastic model definition
| Reaction | Propensity |
|---|---|
|
$ \text{R}_{2}\text{O} \rightarrow \text{R}_{2}\text{O} + \text{M}_{\text{FP}} $ |
$ \text{R}_{2}\text{O} \cdot \text{k}_{\text{s0MFP}} $ |
|
$ \text{M}_{\text{FP}} \rightarrow \text{M}_{\text{FP}} + \text{FP} $ |
$ \text{k}_{\text{sFP}} \cdot \text{M}_{\text{FP}} $ |
|
$ \oslash \rightarrow \text{PlasU} $ |
$ k_{\text{Plas}} \cdot (\frac{\text{PlasM} + \text{PlasU}{Ca})$ |
|
$ \text{FP} \rightarrow \oslash $ |
$ \lambda_{\text{FP}} \cdot \text{FP} $ |
|
$ \text{M}_{\text{FP}} \rightarrow \oslash $ |
$ \lambda_{\text{MFP}} \cdot \text{M}_{\text{FP}} $ |
|
$ \text{PlasU} \rightarrow \text{PlasM} $ |
$ \frac{\text{k}_{\text{cFP}}}{\text{N}_{\text{A}} \cdot \text{V}_{\text{Ecoli}}} \cdot \text{FP} \cdot \text{PlasU} $ |
|
$ \text{PlasU} \rightarrow \oslash $ |
$ \lambda_{\text{Plas}} \cdot \text{PlasU} $ |
|
$ \text{PlasM} \rightarrow \oslash $ |
$ \lambda_{\text{Plas}} \cdot \text{PlasM} $ |
| Parameter | Value |
|---|---|
|
$ \text{Ca} $ |
$ $200$ $ |
|
$ \text{N}_{\text{A}} $ |
$ $6.0221367$ $ |
|
$ \text{V}_{\text{Ecoli}} $ |
$ $8$ $ |
|
$ \text{k}_{\text{s0MFP}} $ |
$ $0.01$ $ |
|
$ \text{k}_{\text{sFP}} $ |
$ $30$ $ |
|
$ \lambda_{\text{MFP}} $ |
$0.462$ |
|
$ \lambda_{\text{FP}} $ |
$ $0.2$ $ |
|
$ \text{k}_{\text{cFP}} $ |
$ $0.0005$ $ |
|
$ \text{k}_{\text{Plas}} $ |
$ $0.00866434$ $ |
|
$ \lambda_{\text{Plas}} $ |
$ $0.00866434$ $ |
| Species name | Initial value |
|---|---|
|
$ \text{R}_{2}\text{O} $ |
$ $200$ $ |
|
$ \text{PlasM} $ |
$ $0$ $ |
|
$ \text{PlasU} $ |
$ $200$ $ |
|
$ \text{FP} $ |
$ 0 $ |
|
$ \text{M}_{\text{FP}} $ |
$0$ |
Discussion
It seems that using a tightly controlled operon is essential. Due to the high rate with which the FP will be able to methylate all bits, controlling the presence of the FP is more important than limiting its catalysis rate.
 "
"


