Team:Colombia/Modeling/Results
From 2012.igem.org
Template:Https://2012.igem.org/User:Tabima
Results
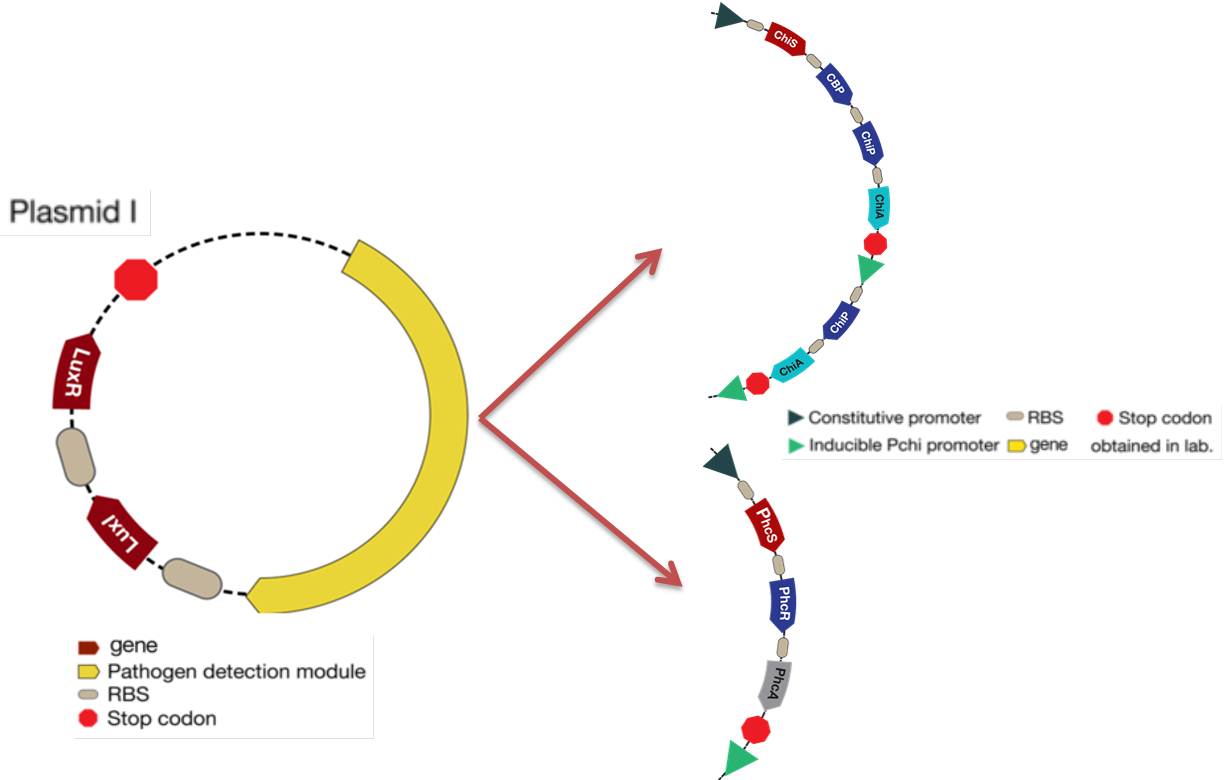
The mathematical model should help the experimental design to optimize the circuit and our case was not the exception. The picture below shows the original design of the circuit.
After doing the simulation for the differential equations we have to make little changes to the proposed system:
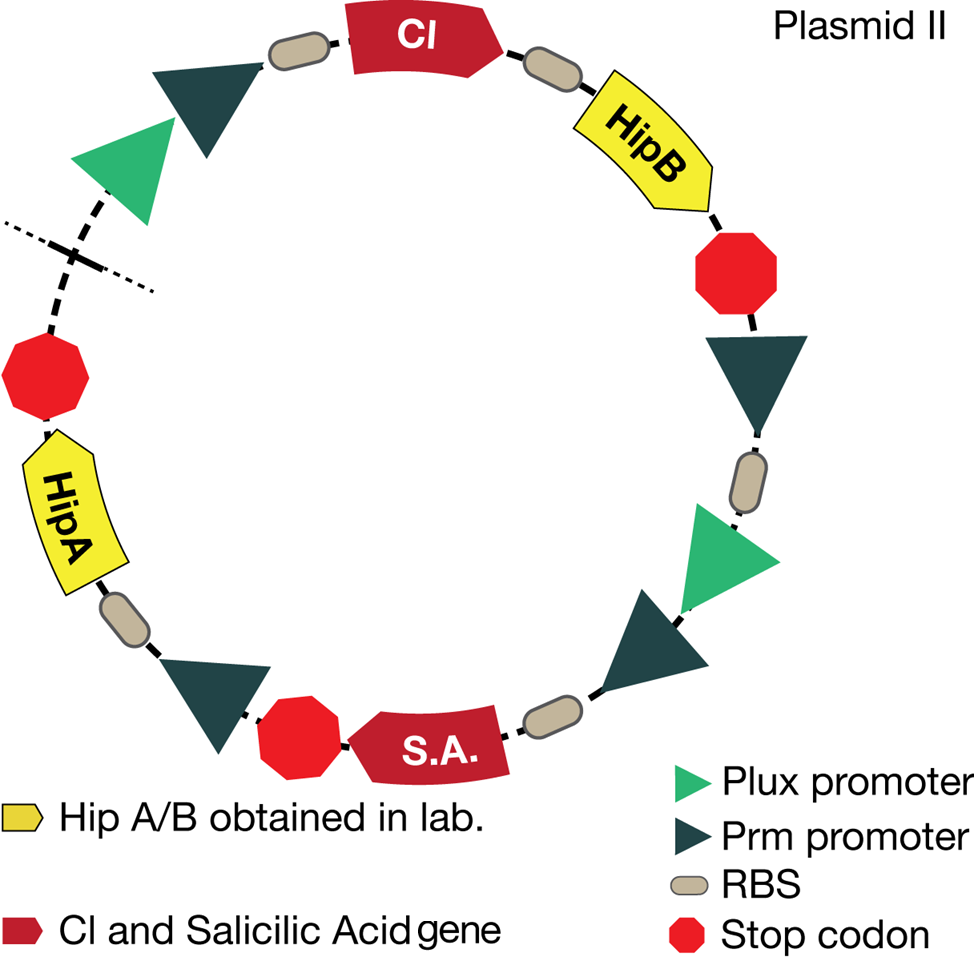
- As you can see there was an unknown promoter for LuxR. First we decided that it was a constitutive promoter but the response curves of the system were not consistent with the reality (LuxR had giant concentrations and the salicylic acid never went up). We wanted this protein to interact with LuxI and turn on the response, so we thought that it may need to be in a similar concentration of LuxI. Then we put it under the same promoter, hence the two proteins will be promoted at the same time.
- Our desired response is the increase of Salicylic Acid when a pest gets near the bacteria. With the original system the salicylic acid increased but not as much as we wanted, so to achieve this goal we tried putting the promoter activated by Lux next to the CI promoter to see if there was an increase. After running the simulation we discovered that this solution optimized the increase of salicylic acid in the response.
- Looking for the right set of parameters we came to the conclusion that the hill constant k (Concentration of the substrate when the the rate of production is half of the maximum production rate) for the promoter activated by Lux had to be 4 times greater than the hill constant for the CI promoter. Which has biological sense; the Lux promoter came from a quorum sensing system, so it needs high concentration of activator because it informs the promoter that there is high cell density. On the other hand the CI promoter box came from a bacteriophage and is used to attack the bacteria as quickly as possible, so it does need small quantities of protein to fully activate its system.
The new system is showed in the picture below:
Differential equations results
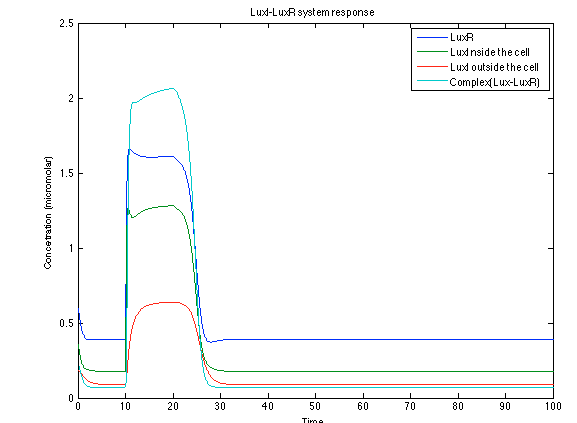
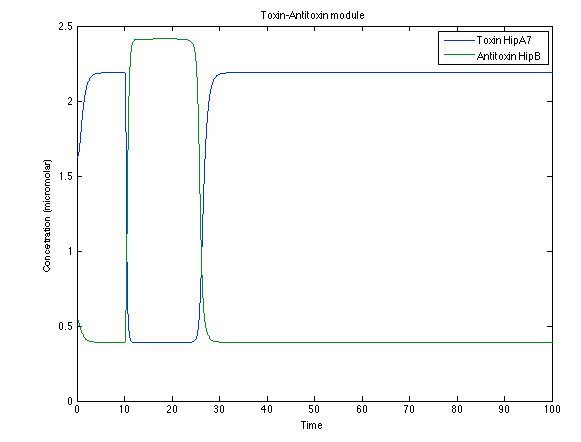
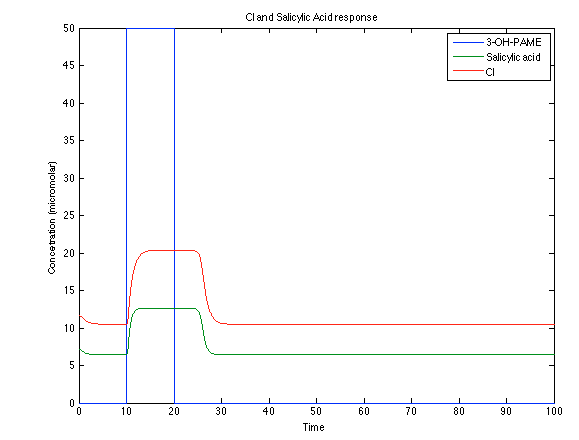
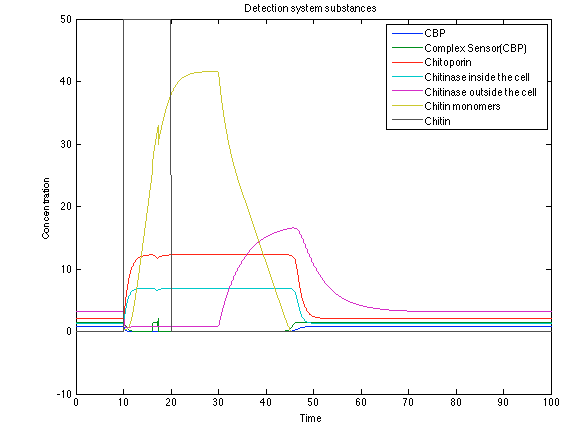
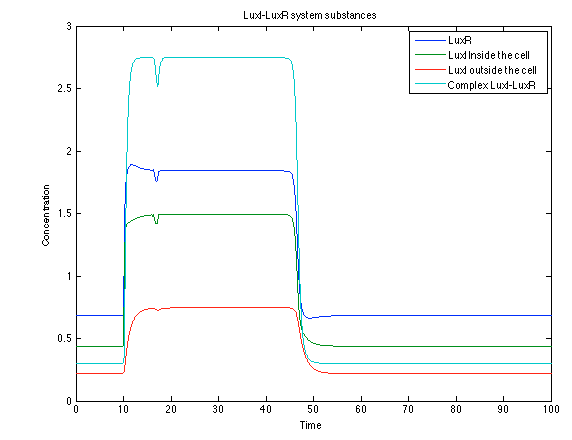
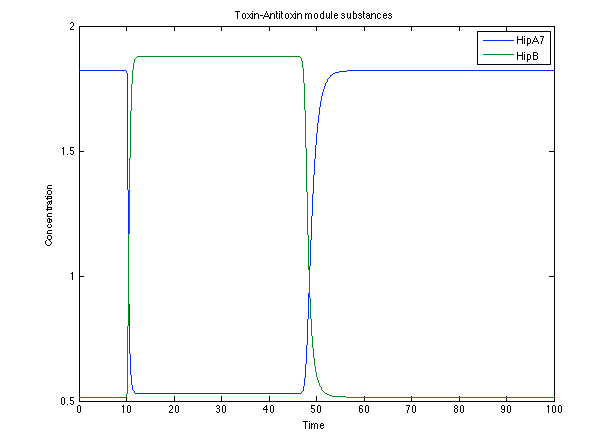
Although the screening of the parameters could not be completely done, we made a manual search for them and found a set that makes the system behave as expected. Here we present the mean response of all the substances in our biological system for one cell. The impulse of the pest was made during the times 10-20.
Ralstonia
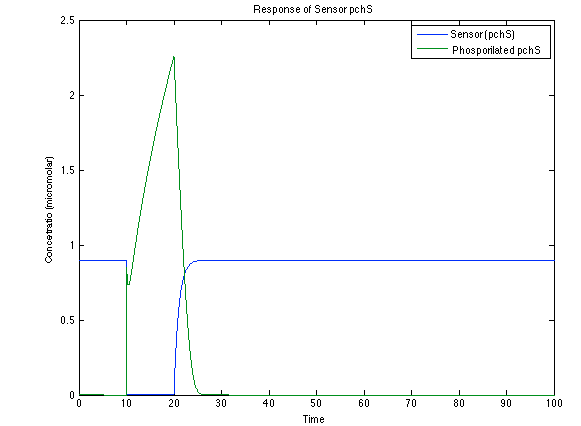
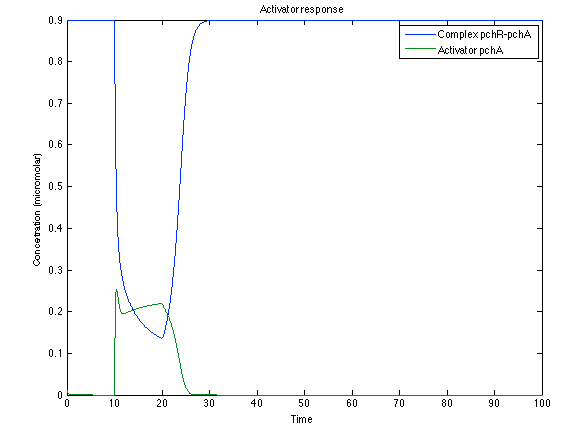
As you see below, when the system is under the presence of 3-OH-PAME the sensor is phosphorylated really fast and the complex phcR-phcA liberates the activator which has a peak and the goes a little down because is with the promoter and its not free. After the impulse is gone everything goes back to normality.
The LuxI- LuxR System shows and increase after it is activated by phcsA
Now, looking at the species of interest, we can see how the antitoxin has greater concentration than the toxin when the 3-OH-PAME appears, this means that the cell is awake and can produce proteins. On the other hand, the Salicylic acid has an increase of almost two fold.
Rust:
When the system is under the presence of chitin you can see how the positive feedback of the chitoporin and chitinase works and make their concentration increase. This has as a consequence the increase of monomers of chitin and the liberation of the sensor that is gonna activate the LuxI and LuxR promoter.
Like we see with the Ralstonia systema the Lux system's concentrations increase when their promoter is activated. The complex LuxI-LuxR has a peak and then goes down a little because it is busy activation of CI and Salicylic Acid.
The compounds od interest behave just like expected. Like in Ralstonia the cell is awake when the chitin is present and the Salicylic Acid has a two fold increase. It is important to see that this system takes more time to go back to the steady state than the Ralstonia's system.
Scripting
Differential equation solver
%THIS CODE CREATE ALL THE DIFFERENTIAL EQUATIONS FOR THE SYSTEM FOR %RASTONIA
function y=ecuaDifR(t,v)
%---------Parameters------%
global alfS %Basal concentration of the sensor phcS
global alfRA %Basal concnetration of the comple pchA-pchR
global alfR %Basal concentration of LuxR
global alfI %Basal concentration of CI
global alfCI %Basal concentration of CI
global alfHA %Basal concnetration of HipA7
global alfHB %Basal concnetration of HipB
global alfAS %Basal concnetration of Salycilic acid
global gammaS %Degradation of the sensor pchS
global gammaRA %Degradation of the complex pchR-pchA
global gammaR %Degradation of LuxR
global gammaI %Degradation of LuxI
global gammaCI %Degradation of CI
global gammaHA %Degradation of HipA7
global gammaHB %Degradation of HipB
global gammaAS %Dergradation of Salycilic acid
global mOHS %Kinetic constant for the detection of 3-OH-PAME by the sensor pchS (phosphorylation)
global mSFR %Kinetic constant for the phosphorylation of the complex pchR-pchA by the sensor
global mA %Kinetic constant for the activation of the promoter by the pchA
global mIR %Kinetic constant for the formation of the complex LuxILuxR
global mI %Constant that represent the union of the complex LuxILuxR with the promoter
global mHAHB %Kinetic constant for the inhibition of HipA7
global betaI %Max production of LuxI
global betaCI %Max production of CI
global betaHB %Max peoduction of HipB
global betaHA %Max production of HipA7
global betaAS %Max production of Salicylic acid
global kA %Constant k of the hill ecuation for the promoter promoted by pchA
global kIR %Constant k of the hill equiation for the promorer prmoted by the complex luxIluxR
global kCI %Constant k of the hill equation for the promoter promoted by CI
global hA %Hill constant for the promoters promoted by pchA
global hIR %Hill constant for the promoter promoted by the complex IR
global hCI %Hill constant fot the promoter CI
global eI %Export factor of LuxI
global jI %Import factor of LuxI
global deltaI %Difusion of LuxI outside the cell
global eAS %Export of Salicylic acid
global numcel %number of cells
if (t<(10) || ((t)>20))
OH=0;
else
OH=15;
end
%------ Variables%------
S=v(1); %Cocentration of the sensor pchS the cell
SF=v(2); %Concentration of phosphorylated sensor the cell
RA=v(3); %Concentration of the comple pchR-pchA
A=v(4); %Concentratio of the promoter avtivator pchA
Ii=v(5); %Concentration of LuxI inside the cell
Io=v(6); %Concentration of LuI outsied the cell
IR=v(7); %Concentration of the complex LuxI-LuxR
R=v(8);%Concentration of the protein CI
CI=v(9);%Concentration of HipA7
HB=v(10);%Concnetratio of HipB
HA=v(11);%Concentration of salicylic acid
AS=v(12); %Concentratio of quitin monomers
%---Equations---%
dS=alfS- gammaS*S - mOHS*OH*S; %Change of the sensor pchS
dSF = mOHS *OH*S - mSFR *SF*RA ; %Change of phosphorylated sensor
dRA=alfRA - gammaRA*RA - mSFR*SF*RA;%Change of the comple pchR-pchA
dA= mSFR*SF*RA-mA*A; %Change of the activator pchA inside the cell
dIi= alfI+ (betaI*(A^hA))/(kA^hA+(A^hA)) -gammaI*Ii +jI*Io- eI*Ii- mIR*Ii*R; %Change of LuxI inside the cell
dIo= numcel*(eI*Ii-jI*Io)-deltaI*Io; %Change of LuxI outside the cell
dIR= mIR*Ii*R - mI*IR; %Change of the complex LuxI luxR
dR= alfR-gammaR*R -mIR*Ii*R +(betaI*(A^hA))/(kA^hA+(A^hA)); %Change of LuxR
dCI= alfCI -gammaCI*CI+ (betaCI*(CI^hCI))/(kCI^hCI+(CI^hCI)) +(betaCI*(IR^hIR))/(kIR^hIR+(IR^hIR));%Change of CI
dHB=alfHB-gammaHB*HB+(betaHB*(CI^hCI))/(kCI^hCI+(CI^hCI))+(betaHB*(IR^hIR))/(kIR^hIR+(IR^hIR))-mHAHB*HA^2*HB^2; %Chanche of HipB
dHA=alfHA-gammaHA*HA+ (betaHA*(CI^hCI))/(kCI^hCI+(CI^hCI))-mHAHB*HA^2*HB^2; %Change of HipA7
dAS=alfAS-gammaAS*AS +(betaAS*(CI^hCI))/(kCI^hCI+(CI^hCI))-eAS*AS+(betaAS*(IR^hIR))/(kIR^hIR+(IR^hIR)); %Change of Salicylic acid
y1(1)=dS;
y1(2)=dSF;
y1(3)=dRA;
y1(4)=dA;
y1(5)=dIi;
y1(6)=dIo;
y1(7)=dIR;
y1(8)=dR;
y1(9)=dCI;
y1(10)=dHB;
y1(11)=dHA;
y1(12)=dAS;
y=y1';
end
 "
"