Team:Shenzhen/Result/YAO.Sensor

Introduction to Modeling Work

    Based on the genetic design of YAO sensor, we modeled the sensor’s functions via the method of modular structured kinetics. In order to model the functions of YAO sensor, we divided the procession into 5 parts:

1. Transport of REX into mitochondrial matrix

2. Activation of REX as a transcription factor with NAD+ and NADH

3. Control of promoter activity by REX

4. Synthesis and degradation of mRNA

5. Synthesis, dilution and degradation of mtGFP

    Finally, the model’s response to dynamic state are tested.

    However, since many parameters for this model are not yet available, the model is not expected to make exact predictions but to give a direct understanding of the functions of the model.

Simulation & Results

• I. Transportation of REX into Mitochondrial Matrix

    We assume that the transcription of SP-REX is constant, SP-REX concentration in cytoplasm is constant, the probably for REX to be transported into each mitochondrion is equal, and mitochondria are of similar size. So with different number of mitochondria in yeast (Nm), the concentration of REX in each mitochondria (Ctf) might differ. Ksp is the transport coefficient of signal peptid which links the XR/Nm with Ctf. For different kinds of signal peptid, Ksp might be different.

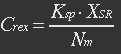(1) XSR: SP-REX concentration in cytoplasm. Nm: Number of mitochondria. Crex: Concentration of REX in Mitochondria. Ksp: Transport coefficient of signal peptid.

• II. Activation of REX as a transcription factor with NAD+ and NADH

NAD+ and NADH can competitively bind to the same site of REX, when NADH binds to REX, REX will be repressed and cannot bind to ROP. Then the transcription function is repressed.

H stands for NADH, REXH stands for REX bidden with NADH. At equilibrium: (2)

N stands for NAD+, REXN stands for REX bidden with NAD+. At equilibrium: (3) NAD+ and NADH are in a balance, so we assumed the total level of NAD+ and NADH in the mitochondria is constant.

REX, REXH and REXN are in a balance, so total level of REX, REXH and REXN equals to Crex.

 (4)

REX which was not bidden with NADH can bind to ROP.

 (5)

REX’ stands for active REX which can bind to ROP. The fraction of active REX acting as repressor is Rf.

 (6)

With (5), (4), (2) and (3) in (6), the fraction becomes

 (7)
Figure 1：Rf responding to different NAD+/NADH ratio.

For plotting of this picture the following parameters were used: assuming K_H = 0,02 μM and K_N = 2 μM since REX NADH affinity > REX NAD affinity [2].

• III. Control of promoter activity by REX

In yeast mitochondria, transcription initiation factor MTF1, combined with RNA polymerase Rpo41, bind to promoter to initiate transcription. It is MTF1 that discerns the promoter region, and the binding of MTF1 on promoter region is reversible. Also the binding of REX on ROP, a DNA region near promoter is also reversible.

P stands for promoter, RP stands for repressor, i.e. REX’, and PRP stands for promoter bidden with repressor. At equilibrium: (8)

P stands for promoter, IF stands for initiation factor i.e. MTF1, and PRP stands for promoter bidden with initiation factor. At equilibrium: (9) Because most of promoters bidden with IF can started transcription, and few of promoters bidden by repressor or not bidden with any TF will transcript. So two coefficient α and β are assumed to reflect the relations.

   (10) 

The fraction of promoters that can be transcribed is Pf.

 (11)

With (10), (8) and (9) in (11), the fraction becomes

 (12)

And

 (13)

So the fraction will be:

 (14)

α=1，Kif=5μM, Krp=5μM, IF=1mM was assumed [5] in this equation.

Figure 2：Pf with different β and changing NAD+/NADH ratio X axis：NAD+/NADH ratio, range from 0 to 500, Y axis：β, range from 0 to 0.2, Z axis：Pf.

Figure 3：Pf with different Crex and changing NAD+/NADH ratio X axis：NAD+/NADH ratio, range from 0 to 500, Y axis：Crex , range from 0mM to 5mM, Z axis：Pf.

Figure 4：Pf with different NAD+/NADH ratio β=0.05, Crex= 2mM was used to plot this picture.

• IV. Synthesis and degradation of mRNA

mRNA is produced from the transcription of the active promoter. Concentration of mitochondrial levels of mRNA (XmRNA) can be derived from the mRNA balance:

Here it is assumed that mRNA is degraded corresponding to a first order reaction and that mRNA is not exported from the cell. The term μXmRNA represents the dilution due to growth. However mRNA is highly unstable and is thus degraded fast. This makes Kdm+μ≈Kdm, simplify the mRNA balance to:

 (16)

It is assumed that when RNA polymerase is efficiently bound to the promoter, the promoter is active and mRNA is transcribed at constant maximum rate . The binding of RNA polymerase is dependent on Pf. In the overall production rate of mRNA, the number of promoters (and genes) Np is also influencing:

 (17)

With (16) and (17), the mRNA balance equation becomes

 (18)

At equilibrium , so

 (19)

Figure 5：XmRNA  with different NAD+/NADH ratio

β=0.05, Vmax = 180 U/h (assuming 75 bases per second, and 1500 bases in gene), Np=10 (1 micron plasmid is used), Kdm=8.3 h-1 (half life = 5 min) was used to plot this picture.

• V. Synthesis, dilution and degradation of GFP

The GFP protein balance:

 (20)

It is assumed that GFP is degraded by first order rate. The dilution cannot be neglected since protein degradation is much slower than mRNA degradation. Furthermore it is assumed that GFP is not transported out of the cell. The protein is synthesized by ribosomes. The number of ribosomes bound to one mRNA (Np) and the protein production rate of the ribosome (Kp) should be taken into account. The number of ribosomes in the cell, ATP and available charged amino acids are assumed to be non-limiting. Taking this into account, the protein synthesis rate can be described as

 (21)

With (21) in (20),

 (22)

At equilibrium , so

 (23)

Nrib = 1. Kp = 288 U/h, assuming 40 amino acids per second. KdGFP = 1.386 h-1 equal to a half time of 30 min [3]. Growth rate = 0.1 h-1

Figure 6：XGFP with different β and changing NAD+/NADH ratio X axis：NAD+/NADH ratio, range from 0 to 500, Y axis：β, range from 0 to 0.2, Z axis：XGFP unit.

Figure 7: XGFP with different Crex and changing NAD+/NADH ratio X axis：NAD+/NADH ratio, range from 0 to 500, Y axis：Crex , range from 0mM to 5mM, Z axis：XGFP unit.

Figure 8: XGFP with different NAD+/NADH ratio

Response for Dynamic states Because the NAD+/NADH level might change in times, so we assume that the change is sinusoidal function as follows: NH=Asin(t/2)+B A=100, B=50, t=0~40. The curve is shown in Figure 9. Then as a result the production of GFP might also changes as a response to the change in NAD+/NADH,

Figure 9: Dynamic change of NAD+/NADH

Figure 10: Response in GFP production

References

[1] Heijnen J.J 2009. Modular structured kinetic models: protein production from genes.

[2] Brekasis, D., Paget, M.S., 2003. A novel sensor of NADH/NAD+ redox poise in Streptomyces coelicolor A3(2). EMBO J. 22, 4856–4865.

[3] Sasson, V., I. Shachrai, et al. 2012. "Mode of regulation and the insulation of bacterial gene expression." Mol Cell 46(4): 399-407.

[4] Mateus and Avery, 2000. Destabilized green fluorescent protein for monitoring dynamic changes in yeast gene expression with flow cytometry. Yeast 2000; 16: 1313±1323.

[5] Deshpande, A. P. and S. S. Patel 2012. "Mechanism of transcription initiation by the yeast mitochondrial RNA polymerase." Biochim Biophys Acta.

[6] Modelling of The Redoxilator by 2009 DTU-DENMARK iGEM team.