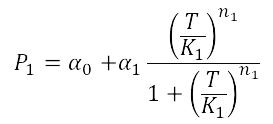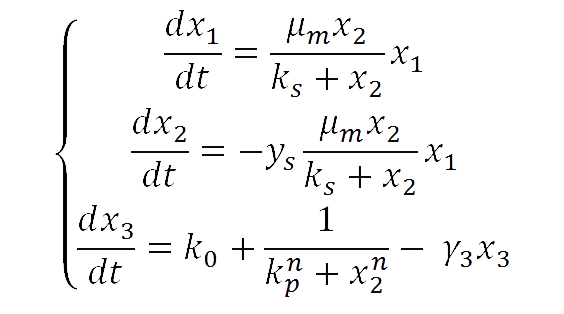"

From 2012.igem.org

Contents 1 Modeling Bacteria 1.1 Are you hot? 2 Modeling Yeast 3 Modeling Cheaters

Modeling Bacteria

Here we modeled several of the Bacteria constructions.

Are you hot?

For the case of the Heat Shock promoter, we decided to model the static transfer function of the Fluorescent Intensity as a result of the Temperature with the folow equation:

Here

In order to estimate the parameters of this model we performed a heat shock experiment.

Analysis corresponding to a heat shock applied during 10 minutes at different tempe-ratures ranging from 20ºC up to 51ºC. For each temperature three samples were tested. Fluorescence Intensity (FI) and optical density (OD) were measured at t1=60 minutes and t2=120 minutes after application of the heat pulse had finished.

The first practical problem we encountered was the lack of enough heating coats. Be-cause of these we took the culture, and we splitted the experiments in two batches. FI and OD were measured at t1=60, and t2=120 for batch number 1, while for batch number 2 the heat shock was delayed by 40 minutes with respect to the first batch. Therefore, measu-rements for batch no.2 were taken at t1=100, and t2=160 minutes respectively.

During this 40 minutes delay, the microorganism was growing. Therefore, the heat shock in batch no. 2 was applied to a larger population than in the case of batch no.1. Consequently, the measurements of FI and DO gave much higher values. This affects the ratio FI/DO, were the two batches can be clearly distinguished (see figure 1).

Modeling Yeast

For our yeast construct: How long have you been fermenting? we propose a phenomenological model to explain the relationship between glucose concentration and fluorescent protein production. The following model was assumed:

where

x₁ = concentration of yeast
x₂ = concentration of glucose
x₃ = fluorescent protein
γ₃ = degradation/dilution rate for the fluorescent protein
k₀ = basal production of fluorescent protein
k_pⁿ = Hill-like coefficient. Notice the exponent n that also appears associated to x₂.

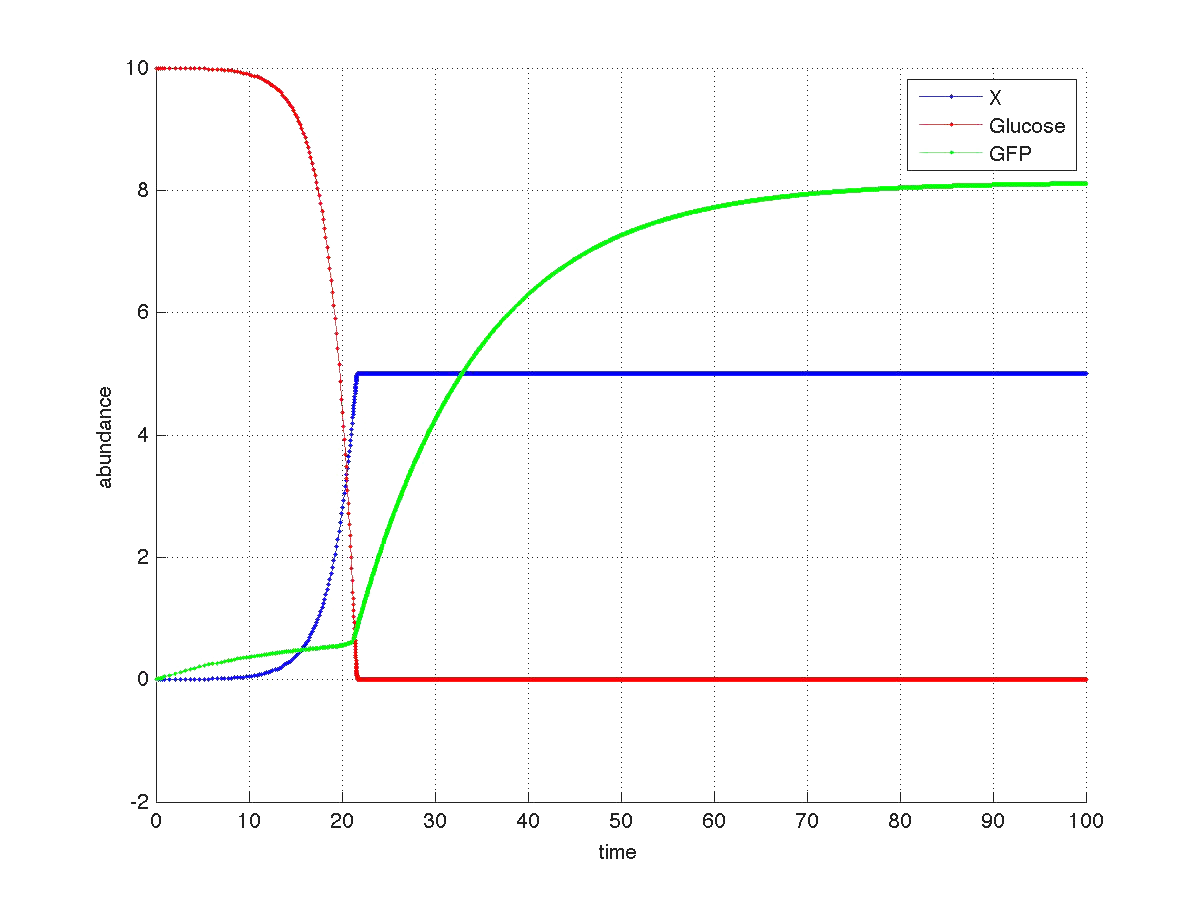
The graph below shows a simulated theoretical time evolution for the three variables.

As observed in the figure, once the glucose is depleted, the concentration of fluorescent protein increases from a basal value.

Modeling Cheaters