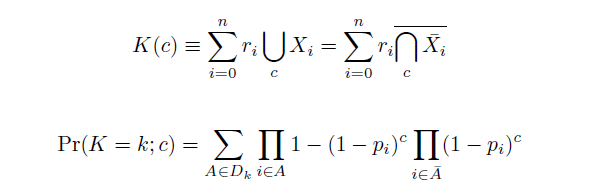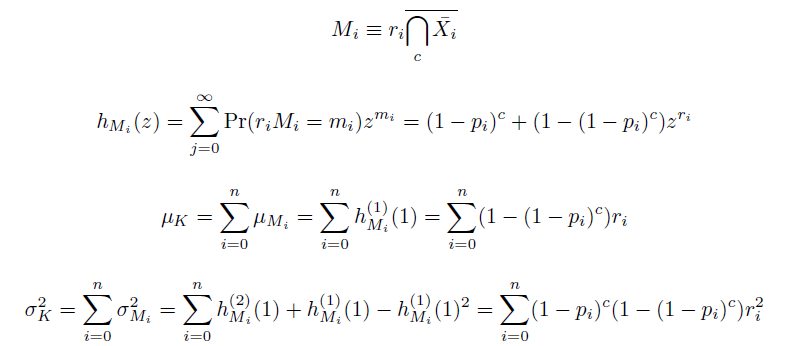Team:Yale/Modeling
From 2012.igem.org
| Line 35: | Line 35: | ||
==References== | ==References== | ||
| - | # Wang, | + | # Wang, H. H., F. J. Isaacs, et al. (2009). "Programming cells by multiplex genome engineering and accelerated evolution." Nature 460(7257): 894-898. |
| - | # | + | # Wadycki, W. J., B. K. Shah, et al. (1973). "Letters to the Editor." The American Statistician 27(3): 123-127. |
| - | # Horowitz and Sahni 1974 | + | # Horowitz, E. and S. Sahni (1974). "Computing Partitions with Applications to the Knapsack Problem." J. ACM 21(2): 277-292. |
Revision as of 00:45, 27 October 2012
| Home | Team | Official Team Profile | Project | Parts Submitted to the Registry | Modeling | Notebook | Safety | Attributions |
|---|
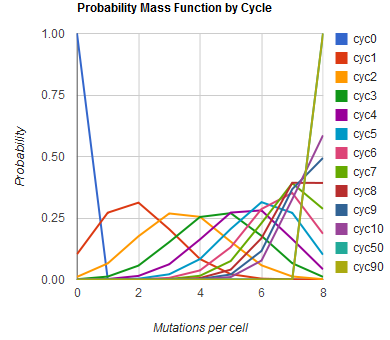
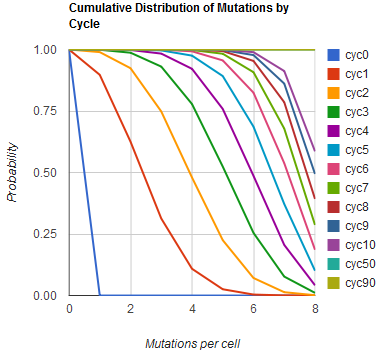
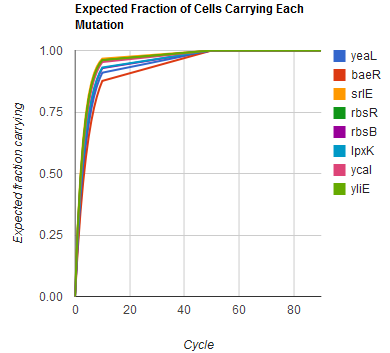
Modeling the evolution of a population during MAGE
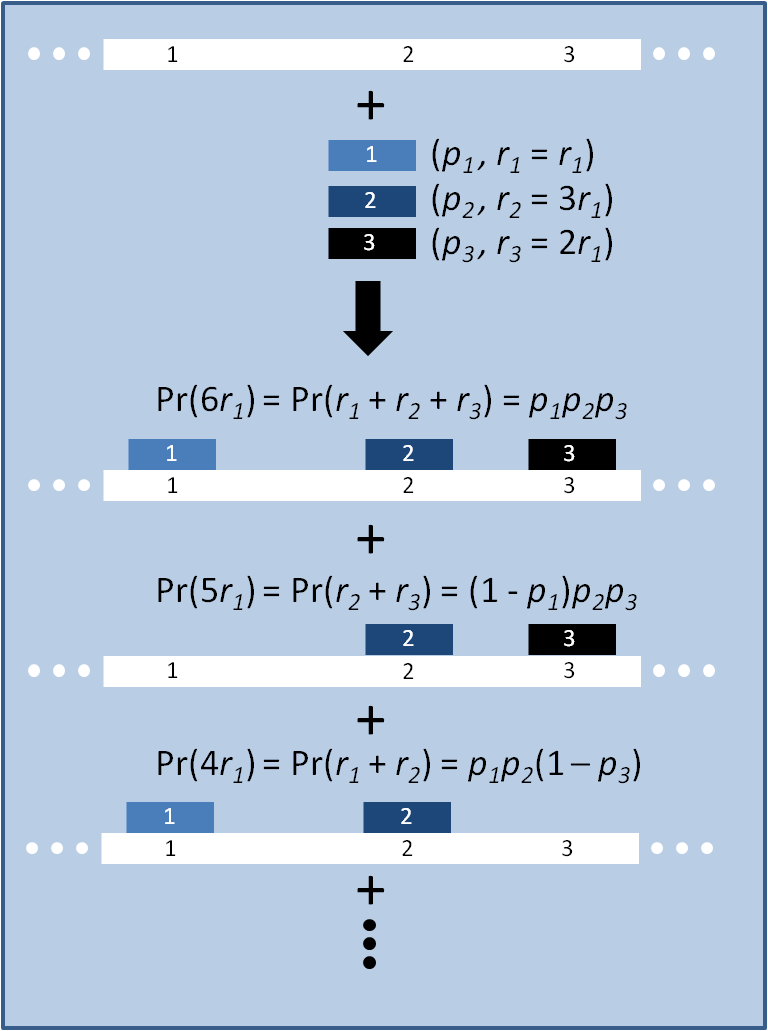
The distribution of specific mutations in MAGE is a stochastic process that we model as as a function of each oligo's predicted efficiency of allelic replacement (which can be estimated in E. coli [1]), assuming that each mutation event is binary and exclusive. Then a population after c cycles is a weighted sum of n Bernoulli trials, each zero if the oligo does not mutate its target i and otherwise equal to the number r of mutations it induces. Given efficiencies of allelic replacement p, this probability mass function becomes:
In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, but we optimized our algorithm to avoid slowdowns by using a recursive formula [2] for the occasional, simpler case when all oligos carry the same number of mutations, and in other cases a branched, dynammic programming algorithm [3].
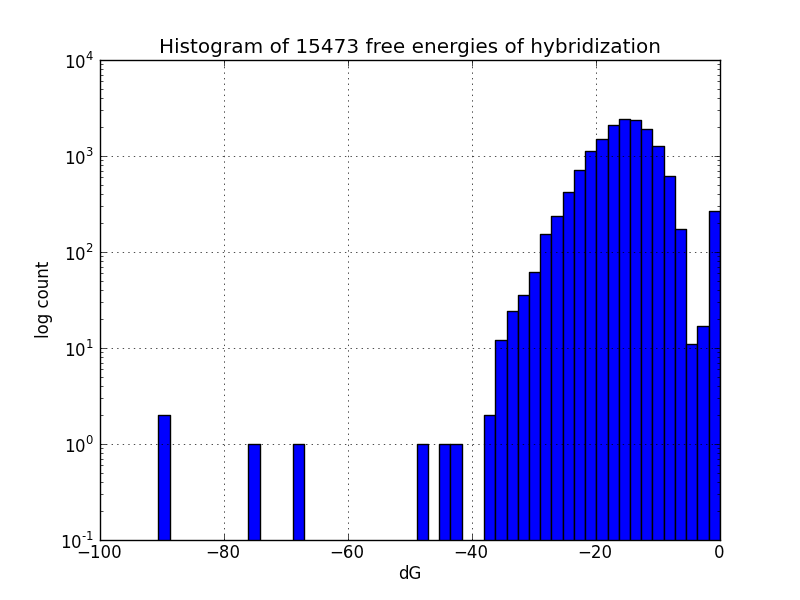
Survey for off-target binding sites
Not all MAGE-induced mutations will be at the intended sites; to identify likely unintended mutations, we scripted a search of the genome using BLAST+ to find subsequences with four base pairs or more matching oligos in the MAGE oligo pool, and estimates the change in Gibbs energy likely upon hybridization at each such off-target pairing, using the UNAFold software package.
Both of these scripts will be bundled into an cloud-based tool for genomic engineering (unpublished work).
References
- Wang, H. H., F. J. Isaacs, et al. (2009). "Programming cells by multiplex genome engineering and accelerated evolution." Nature 460(7257): 894-898.
- Wadycki, W. J., B. K. Shah, et al. (1973). "Letters to the Editor." The American Statistician 27(3): 123-127.
- Horowitz, E. and S. Sahni (1974). "Computing Partitions with Applications to the Knapsack Problem." J. ACM 21(2): 277-292.
 "
"