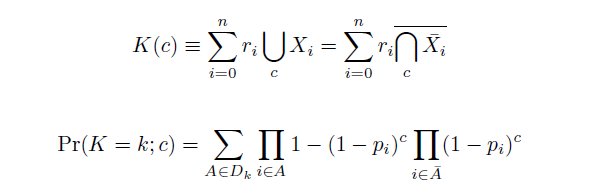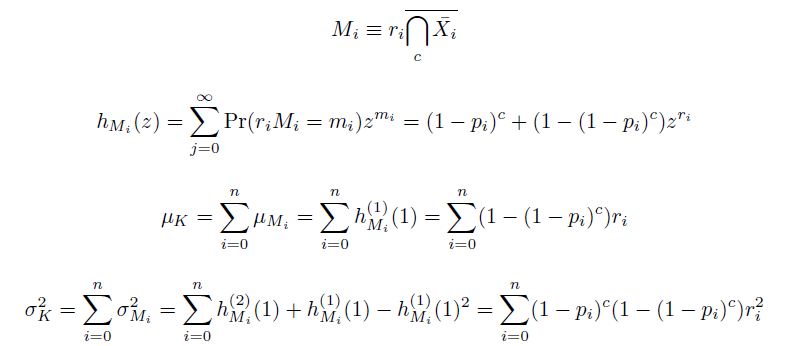Team:Yale/Modeling
From 2012.igem.org
(→Modeling the evolution of a population during MAGE) |
|||
| Line 22: | Line 22: | ||
In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, but we optimized our algorithm to avoid slowdowns by using a recursive formula [2] for the occasional, simpler case when all oligos carry the same number of mutations, and in other cases a branched, dynammic programming algorithm [3]. | In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, but we optimized our algorithm to avoid slowdowns by using a recursive formula [2] for the occasional, simpler case when all oligos carry the same number of mutations, and in other cases a branched, dynammic programming algorithm [3]. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==Survey for off-target binding sites== | ==Survey for off-target binding sites== | ||
| Line 38: | Line 33: | ||
Both of these scripts will be bundled into an cloud-based tool for genomic engineering (unpublished work). | Both of these scripts will be bundled into an cloud-based tool for genomic engineering (unpublished work). | ||
| + | |||
| + | ==References== | ||
| + | # Wang, HH and Isaacs, FJ et al. Programming cells by multiplex genome engineering and accelerated evolution. Nature 2009. | ||
| + | # Wadyicki, Shah et al. 1973. | ||
| + | # Horowitz and Sahni 1974 | ||
Revision as of 00:32, 27 October 2012
| Home | Team | Official Team Profile | Project | Parts Submitted to the Registry | Modeling | Notebook | Safety | Attributions |
|---|
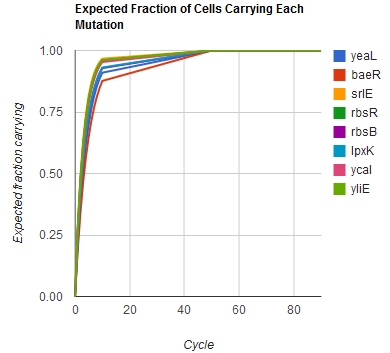
Modeling the evolution of a population during MAGE
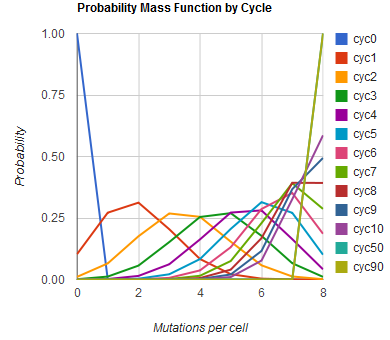
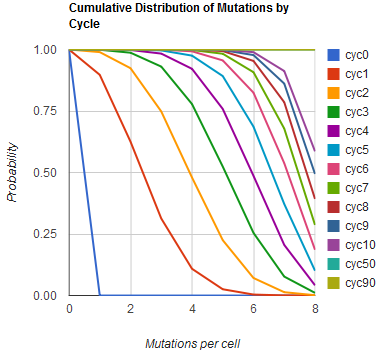
The distribution of specific mutations in MAGE is a stochastic process that we model as as a function of each oligo's predicted efficiency of allelic replacement (which can be estimated in E. coli [1]), assuming that each mutation event is binary and exclusive. Then a population after c cycles is a weighted sum of n Bernoulli trials, each zero if the oligo does not mutate its target i and otherwise equal to the number r of mutations it induces. Given efficiencies of allelic replacement p, this probability mass function becomes:
In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, but we optimized our algorithm to avoid slowdowns by using a recursive formula [2] for the occasional, simpler case when all oligos carry the same number of mutations, and in other cases a branched, dynammic programming algorithm [3].
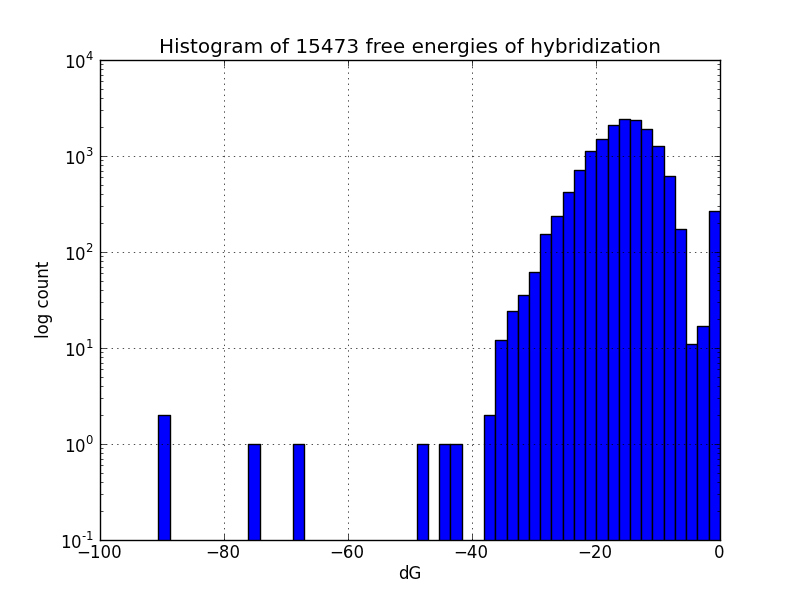
Survey for off-target binding sites
Not all MAGE-induced mutations will be at the intended sites; to identify likely unintended mutations, we scripted a search of the genome using BLAST+ to find subsequences with four base pairs or more matching oligos in the MAGE oligo pool, and estimates the change in Gibbs energy likely upon hybridization at each such off-target pairing, using the UNAFold software package.
Both of these scripts will be bundled into an cloud-based tool for genomic engineering (unpublished work).
References
- Wang, HH and Isaacs, FJ et al. Programming cells by multiplex genome engineering and accelerated evolution. Nature 2009.
- Wadyicki, Shah et al. 1973.
- Horowitz and Sahni 1974
 "
"