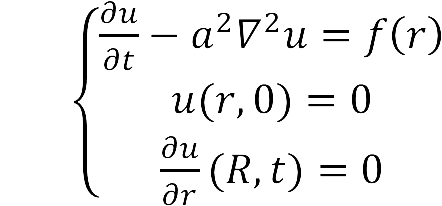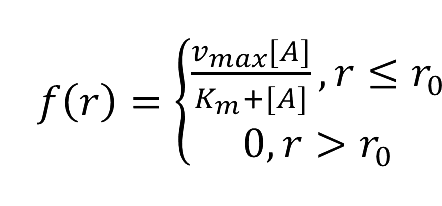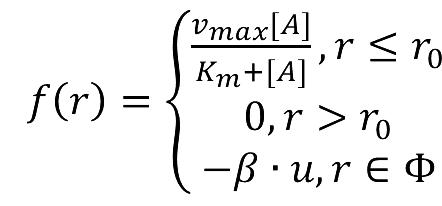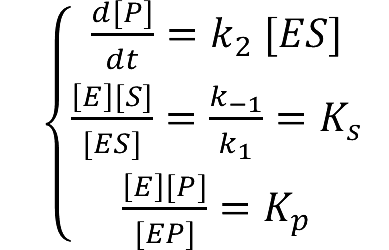In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.
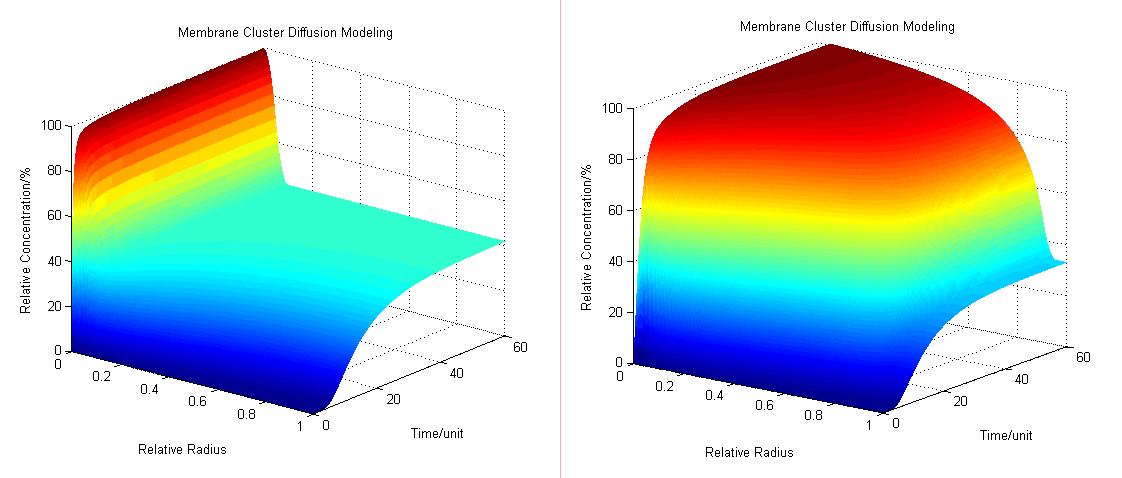
Mathematical modeling is a useful tool for understanding how a bio-system works and how to improve it. We build a mathematical model mainly based on the mechanism of the involved biochemical reaction. Here we focus on the dynamic process of membrane protein cluster in order to reveal how the system works over time.
PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, or elasticity. Defined by the PDE, the variable describing the phenomena can be solved according to different boundary values.
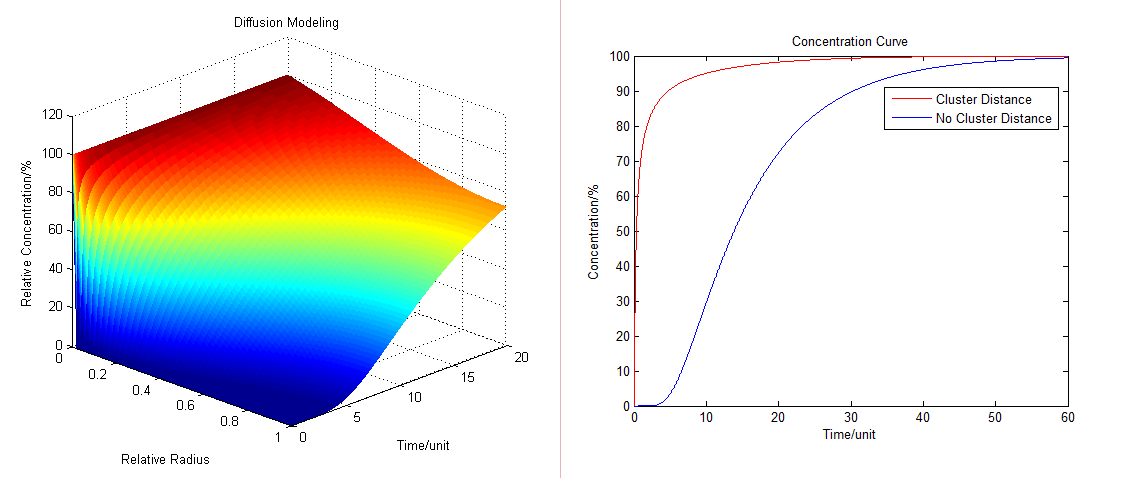
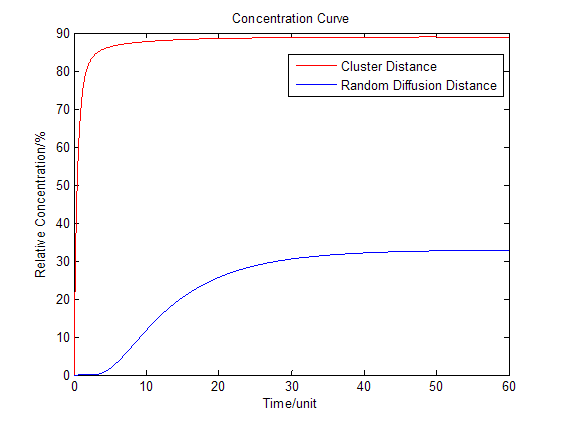
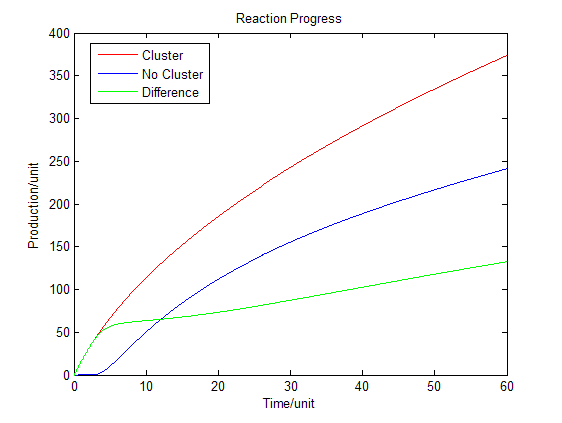
Based on diffusion equation, by solving it under different boundary values, we found that the cluster system can increase production significantly.
As we assumed that the area we chose is a closed region, the products cannot diffuse to the outer side of the area. However when we are using the system in the situation of industry, most of the products can diffuse through the membrane and enter the culture medium. Under this situation the equilibrium will be changed. Reaction beside the membrane barrier can enhance the process the trans-membrane transportation as the concentration of products is much higher than the cytoplasm. Consequently there will be a dramatic increase in product amount.
 "
"