Team:Potsdam Bioware/Project/Modeling
From 2012.igem.org
(→Parameter Analysis) |
(→Parameter Analysis) |
||
| Line 260: | Line 260: | ||
100 | 100 | ||
</a> | </a> | ||
| - | </td><td align="center" valign="middle"> | + | </td><td align="center" valign="middle" bgcolor="#FFFF00"> |
<a href="https://static.igem.org/mediawiki/2012/f/f3/UP12_modeling_InitialV1000.jpg" | <a href="https://static.igem.org/mediawiki/2012/f/f3/UP12_modeling_InitialV1000.jpg" | ||
onmouseover="button01.src=image3.src"> | onmouseover="button01.src=image3.src"> | ||
Revision as of 18:24, 26 September 2012
Modeling
Contents |
Modeling
Abstract
Introducion
Modeling is a powerful tool to understand complex interactions or processes. We created a model to illustrate our selection system and to get a better understanding of its behavior under different conditions. Thereby, we wanted to answer two main questions:
- At which time point selection is successful?
- How many antibody presenting cells and how many virus particles do we need at the beginning?
To answer these questions we did both deterministic and stochastic modeling using MATLAB. Furthermore, we did a huge parameter analysis for each model to check what kind of influence each parameter has on our selection system.
Simplest Model
Reaction Scheme
We built a simple model of our in vivo selection system which includes the reactions that are the most equivalent to our project. The following scheme (Fig. 1) shows the reactions occurring in our model.
Species:
reaction rates:
|
Our system starts with the antibody presenting cell exhibiting a cell division rate (kdiv) and a cell death rate (kdeath). Due to expression of AID the antibodies get mutated and with a particular rate (kmut) we get a mutated cell presenting more affine antibodies. Thereby, the virus infection is changed and is able to trigger the selection of mutated cells. We can distinguish between two different cases.
Within the first case, the infection rate of the virus to the mutated cell (kintM) is improved compared to the infection rate to WT cell (kintC). In this case through the virus infection a positive stimulus can be mediated, resulting in both a higher cell division rate (kdivAinf) and/or a lower cell death rate (kdeathAinf).
In case two, the infection rate of the virus to the mutated cell is decreased compared to the infection rate to WT cell C (kintM < kintC). Hence, through the virus infection, a negative stimulus can be mediated, resulting in a lower cell division rate (kdivAinf) or a higher cell death rate (kdeathAinf) or even both. The stimulus due to virus infection gets lost while the process proceeds (kloss). This means that the virus infection is steadily required for those stimuli.
(Due to the experimental observation which show that without an antibody no infection can be seen, we assume that with a better antibody on the cell surface the infection rate by the virus is improved compared to the WT cell. This means we should apply a positive selection system. For this we use antibiotics as selection pressure and antibiotic resistance as positive stimulus through virus infection. Therefore, for modeling we used low cell division rate compared to cell death rate and a high cell division rate after virus infection.)
Deterministic Model
For deterministic modeling we write the reactions as ordinary differential equations (ODE´s) (see Fig. 2) and solved them using MATLAB. Because we only had marginal information about parameter values we estimate them and did a large parameter analysis (see below).
ODE´s
Results
For calculation in MATLAB we used the following parameter values as reference state. In figure 3 time dependent concentrations of each species are shown.
Reference state:
|
We start with a 10-fold higher concentration of virus (shown in dark blue) compared to WT cell (shown in green). Concentration of WT cells decreases because of cell death due to antibiotic pressure. Virus concentration decreases because of infection of cells. WT cells were only marginal infected resulting in low concentration of infected WT cells (shown in red). After about 100 h mutated cells arose and were directly infected, because of high infection rate and high virus concentration. This leads to increased concentration of infected mutated cells and mutated cells respectively, due to stimulus of virus infection (antibiotic resistance). From that time point concentration of virus decreases rapidly and gets down to zero at about 200 h. Because of the lack of virus, cells were not infected and will get no positive stimulus. Due to continuous antibiotic pressure, cell concentration of both mutated and WT cells decreases.
To act against these decreases we performed two time steps shown in figure 4. In the first time step high selection pressure via antibiotics was applied. After successful selection, the antibiotic pressure was removed (e.g. by medium exchange) and therefore cell concentration increases due to higher cell division rate than cell death rate. Media:UP12-det-twostepmodel.m
Parameter Analysis
Because we had only marginal information about parameter values we did a large parameter analysis. We wanted to know how each parameter influences the selection system. Therefore, we looked at the influence on success of selection and the influence on time scale. For this analysis we observed the ratio of mutated cells to WT cells (ratio of M to C). For a successful selection the ratio of mutated cells to WT cells should be higher than one and as high as possible. Media:UP12-det-parameteranalysis.m
One dimensional (1D)
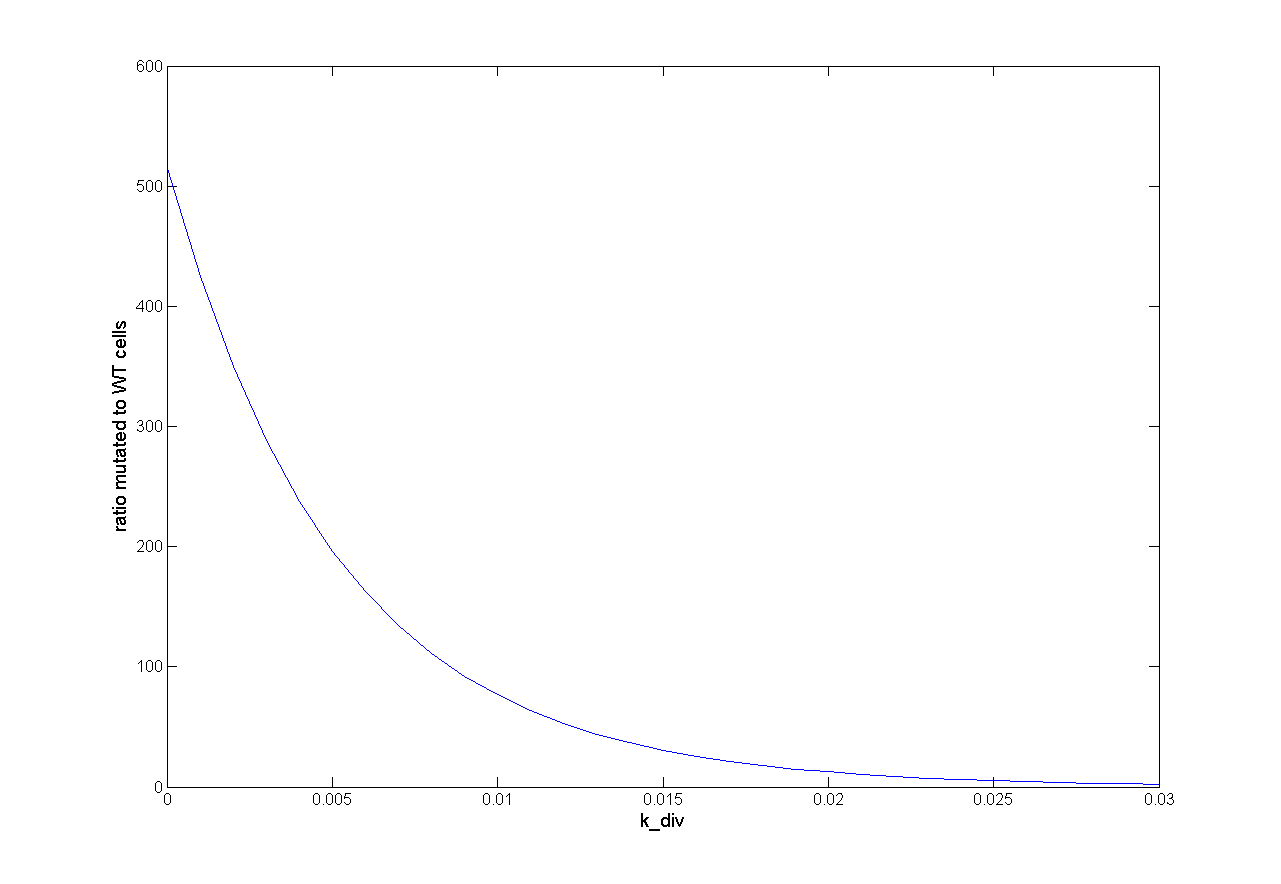
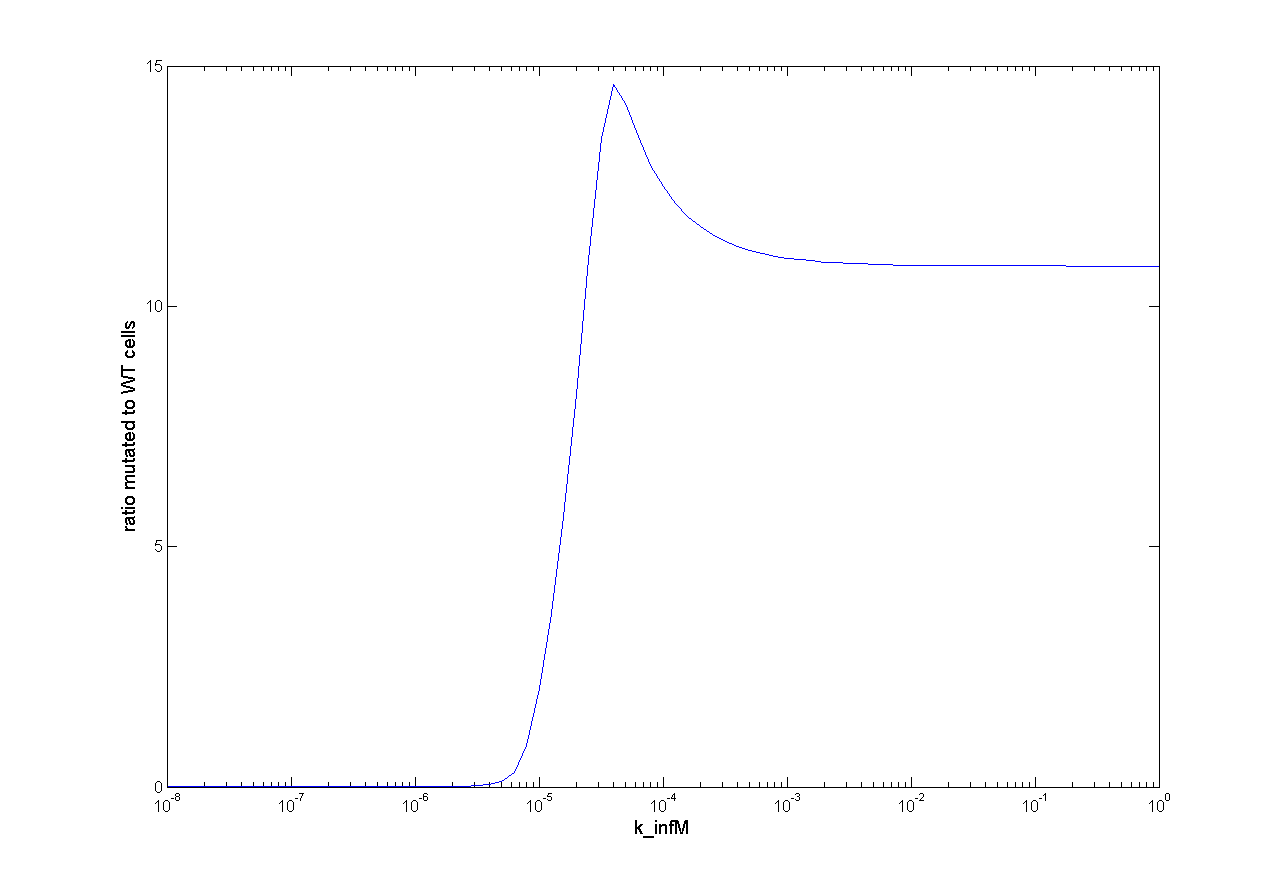
For one dimensional analysis we changed each parameter holding all other parameters constant at reference state and observed the ratio of mutated cells to WT cells. Following results were obtained:
Figure x: One dimensional analysis of all parameters. The ratio mutated to wt cells is plotted against the parameter value
Two dimensional (2D)
For two dimensional analysis we changed two parameter holding all other parameters constant at reference state and observed the ratio of mutated cells to WT cells. Following results were obtained:
Time dependencies
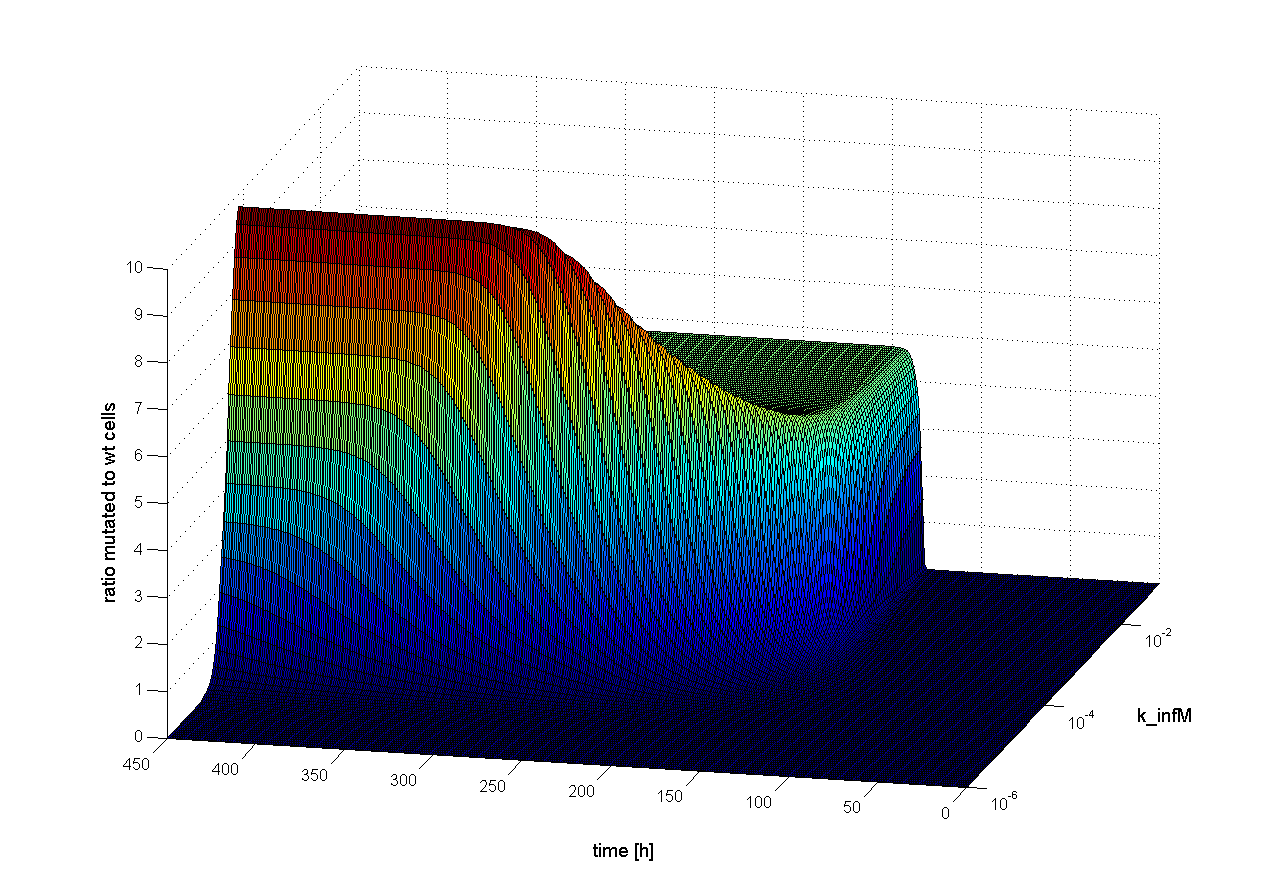
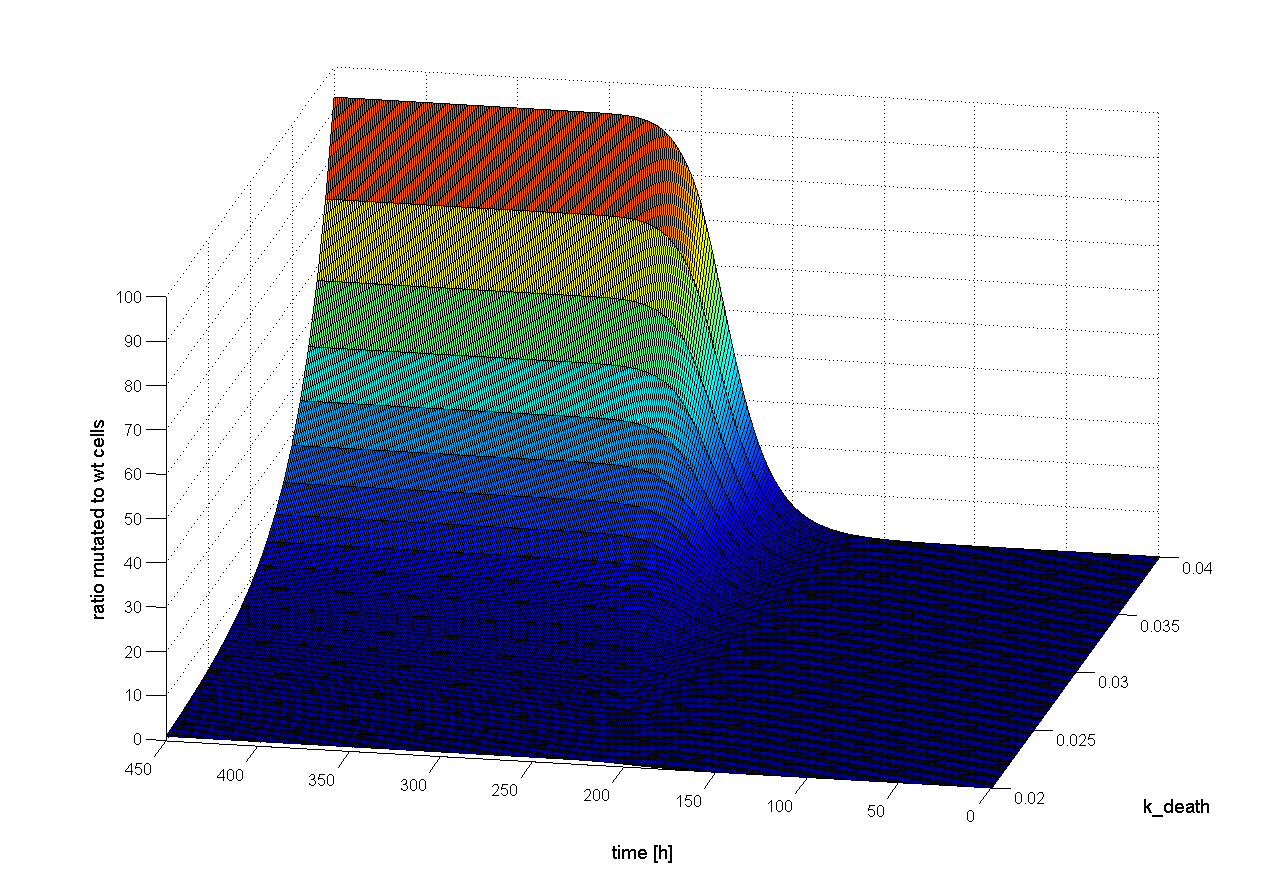
To find out which parameter is time dependent, we observed the ratio of mutated cells to WT cells over the time changing only one parameter. If the parameter is time dependent, changes in the ratio of mutated cells to WT cells should be observed earlier or later. Following results were obtained:
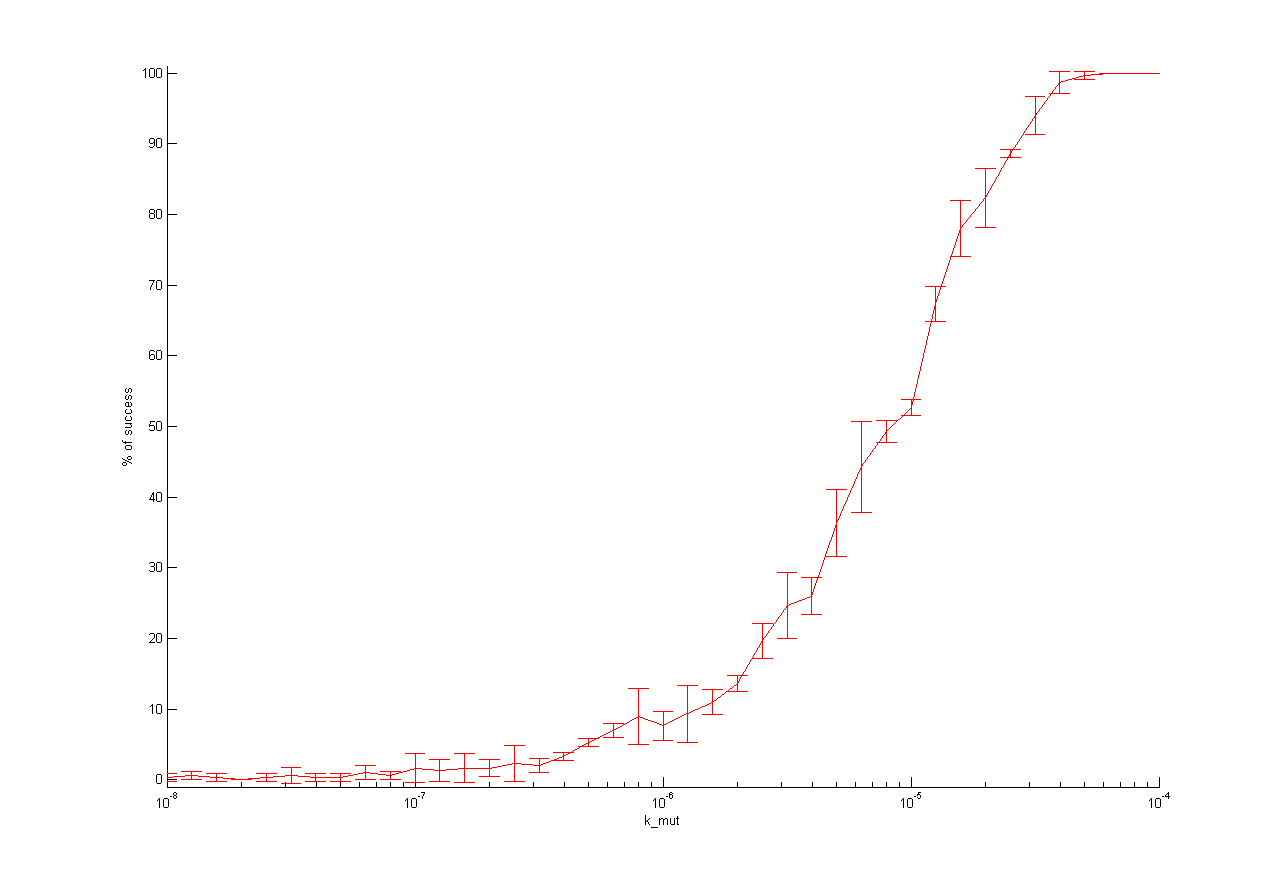
We observed that different parameters have different influence on time flow of our selection systems. A high influence on time flow have the mutation rate (k_mut), the infection rate for mutated cells (k_infM) and the cell division rate after virus infection (k_divAinf). On Figure x for example you can see that the higher the mutation rate the earlier we get a higher ratio of mutated to WT cells. This means selection of mutated cells presenting a high affine antibody happens earlier. Also the higher the infection rate for mutated cells or the cell division after infection, the earlier we get a selection success (Figure x and y).
|
The parameter k_loss have only low influence on time flow of selection system (see Figure x). The higher rate of the loss of viral genes (the positive signal), the later selection is successful. The cell division rate (k_div), the cell death rate (k_death) and the infection rate with WT cells (k_infC) are time independent (see Figure x). These parameters have only an influence on success of our selection system, but not on the time point when selection is finished. |
Stochastic Model
Stochastic modeling is necessary if one or more species occur in low amounts. In this case reactions are random events that lead to fluctuating concentrations of species which can be characterized by different results in several experiments or runs, respectively. In our selection system we get only low amount of mutated cells due to low mutation rate. Because of this and because of some peculiar behavior of the deterministic model we did stochastic modeling. For this we used the “simbiology” - tool of MATLAB. We built our model in the “simbiology” - tool and calculated stochastic kinetics using the stochastic simulation algorithm (SSA). This algorithm efficiently generates individual simulations that are consistent with the chemical master equation (CME). The greatest advantage of this algorithm is the precision. [1]
We used the same parameters like in deterministic modeling.
Results
In figure x the concentration of each species is plotted against the time. We see nearly the same results compared to deterministic model. The concentrations of virus and WT cells decrease. From a certain time point the concentrations of infected mutated cells and mutated cells increase while virus is available. When virus concentration becomes zero, the concentrations of infected mutated cells and mutated cells decrease.
The difference between deterministic and stochastic model becomes obvious when we run the stochastic calculation several times (see figure x). Figure x shows that the time point when mutated cells were selected and their concentration was greater than non-mutated cells, differ in large scales. Furthermore, in some runs mutated cells did not arise, meaning that sometimes the selection was not successful. This is a typical result and can be explained by the stochastic behavior. Because of low concentration of mutated cells sometimes they become extinct by random events and no selection takes place.
Parameter Analysis
For stochastic modeling we also did parameter analysis for both one and two dimensional. We change one or two parameters while holding the other parameters constant and run the calculation 3x100 times counting the successful selections. As a successful selection we defined a ratio of mutated cells to WT cells greater than 1.
Media:UP12-stoch-parameteranalysis.m

|

|
One dimensional (1D)
In Figure x for each parameter, the percentage of successful selections is plotted against the parameter values.
Figure x: One dimensional analysis of all parameters. The percentage of selection success is plotted against the parameter value
two dimensional
Summary
(Stochastic results showed that the selection is finished on random time points after 100 h or later (see Fig. X A). Furthermore, the analysis of initial concentrations of WT cell and virus revealed that there is an optimum for initial concentrations of WT cell and virus (see Fig. X B). Both too less and too excessive concentrations prevent the success of the selection system)
 "
"