Team:USP-UNESP-Brazil/Associative Memory/Background
From 2012.igem.org
(→Biological Mechanism) |
(→Hopfield Associative Memory Networks) |
||
| Line 2: | Line 2: | ||
===Hopfield Associative Memory Networks=== | ===Hopfield Associative Memory Networks=== | ||
| - | The idea of this project is based on the associative memory network introduced by J.J. Hopfield in the 80’s [http://en.wikipedia.org/wiki/Hopfield_network]. The structure of a Hopfield network is simple, all neurons are interconnected | + | The idea of this project is based on the associative memory network introduced by J.J. Hopfield in the 80’s [http://en.wikipedia.org/wiki/Hopfield_network]. The structure of a Hopfield network is simple, all neurons are interconnected, what brings some interesting memory properties and provide a model for understanding human memory. |
| - | + | We have chosen to built a Hopfield network because of its simplicity and robustness. The same methodology can be used to the construction of networks with different architectures, such as the called “perceptrons” [http://en.wikipedia.org/wiki/Perceptron]. In contrast to a Hopfield network, a perceptron is commonly used as a classifier and its structure is feed-forward. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | We have chosen to built a Hopfield network because of its simplicity and robustness. The same methodology can be used to the construction of networks with | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
===Biological Mechanism=== | ===Biological Mechanism=== | ||
Revision as of 14:18, 26 September 2012
 Introduction
Introduction Project Overview
Project Overview Plasmid Plug&Play
Plasmid Plug&Play Associative Memory
Associative MemoryNetwork
 Extras
ExtrasHopfield Associative Memory Networks
The idea of this project is based on the associative memory network introduced by J.J. Hopfield in the 80’s [http://en.wikipedia.org/wiki/Hopfield_network]. The structure of a Hopfield network is simple, all neurons are interconnected, what brings some interesting memory properties and provide a model for understanding human memory.
We have chosen to built a Hopfield network because of its simplicity and robustness. The same methodology can be used to the construction of networks with different architectures, such as the called “perceptrons” [http://en.wikipedia.org/wiki/Perceptron]. In contrast to a Hopfield network, a perceptron is commonly used as a classifier and its structure is feed-forward.
Biological Mechanism
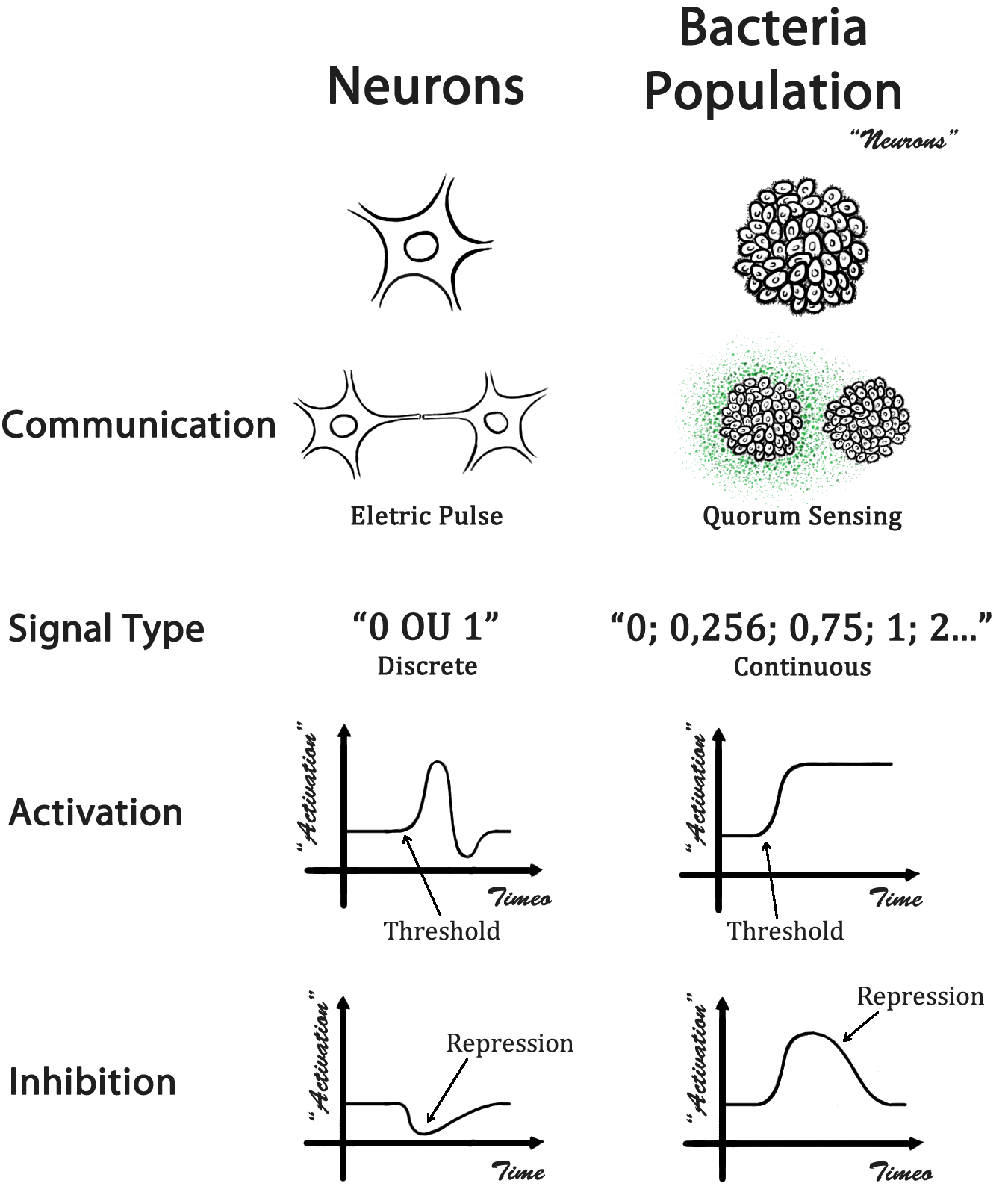
In a biological neural network, the cells occupy a specific location and the information is addressed through a direct physical contact - the neuron axonal projections. In our case, a population of bacteria represents a single neuron and the information is addressed by a quorum sensing molecule (QSM). With different QSM, it is possible to address the information in a specific manner. A comparison between a biological neural network and our design is presented in Fig 1.
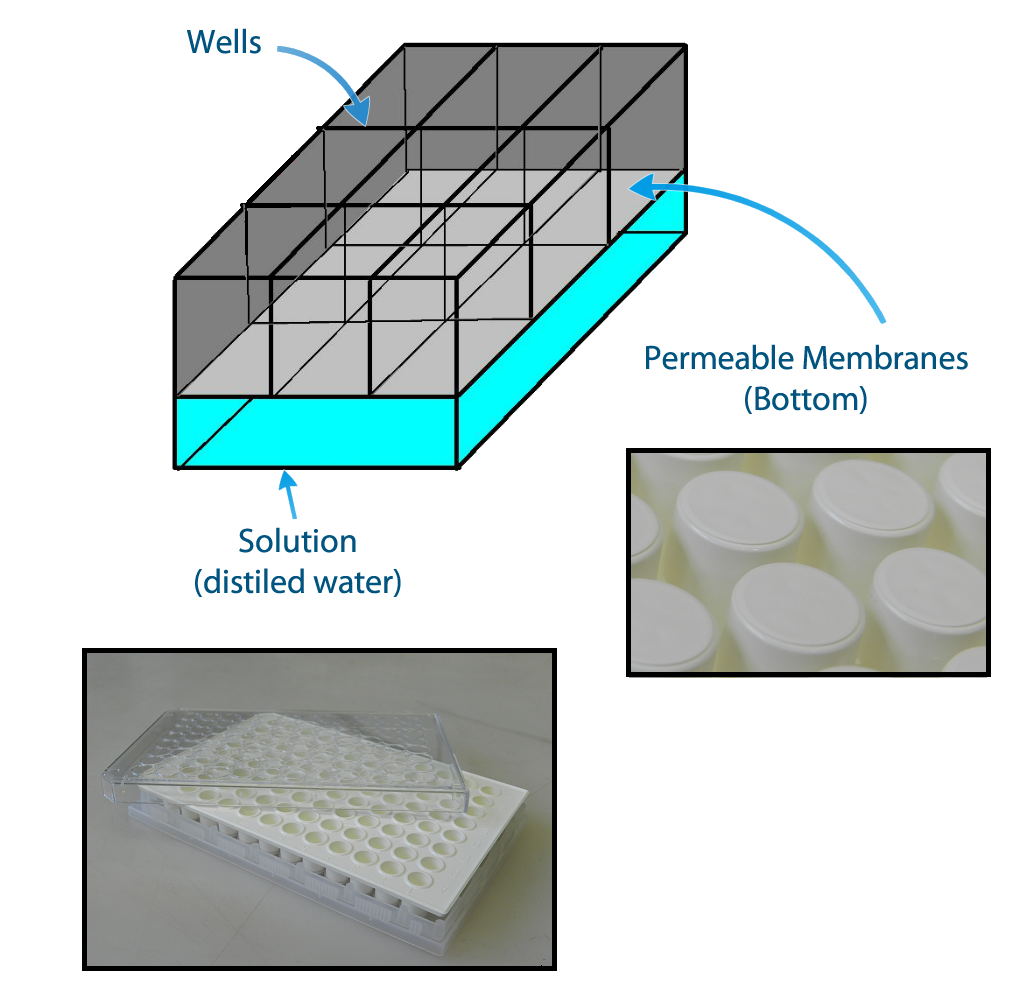
In order to be able to measure if one population is activated we planned the construction of a device to make 9 E.coli populations to communicate with each other keeping a position in space. This device enables the communication not only of neighbors but also of all the populations. Figure 2 shows a construction of the system that can enable an efficient communication between the populations of different positions of the network, even if it is physically separating them.
The device can be easily constructed using a plate of 96 wells with membranes attached to the bottom. The membranes allow the diffusion of the quorum sensing substances and prevent the flux of bacterial populations between the wells.
Genetic Construction
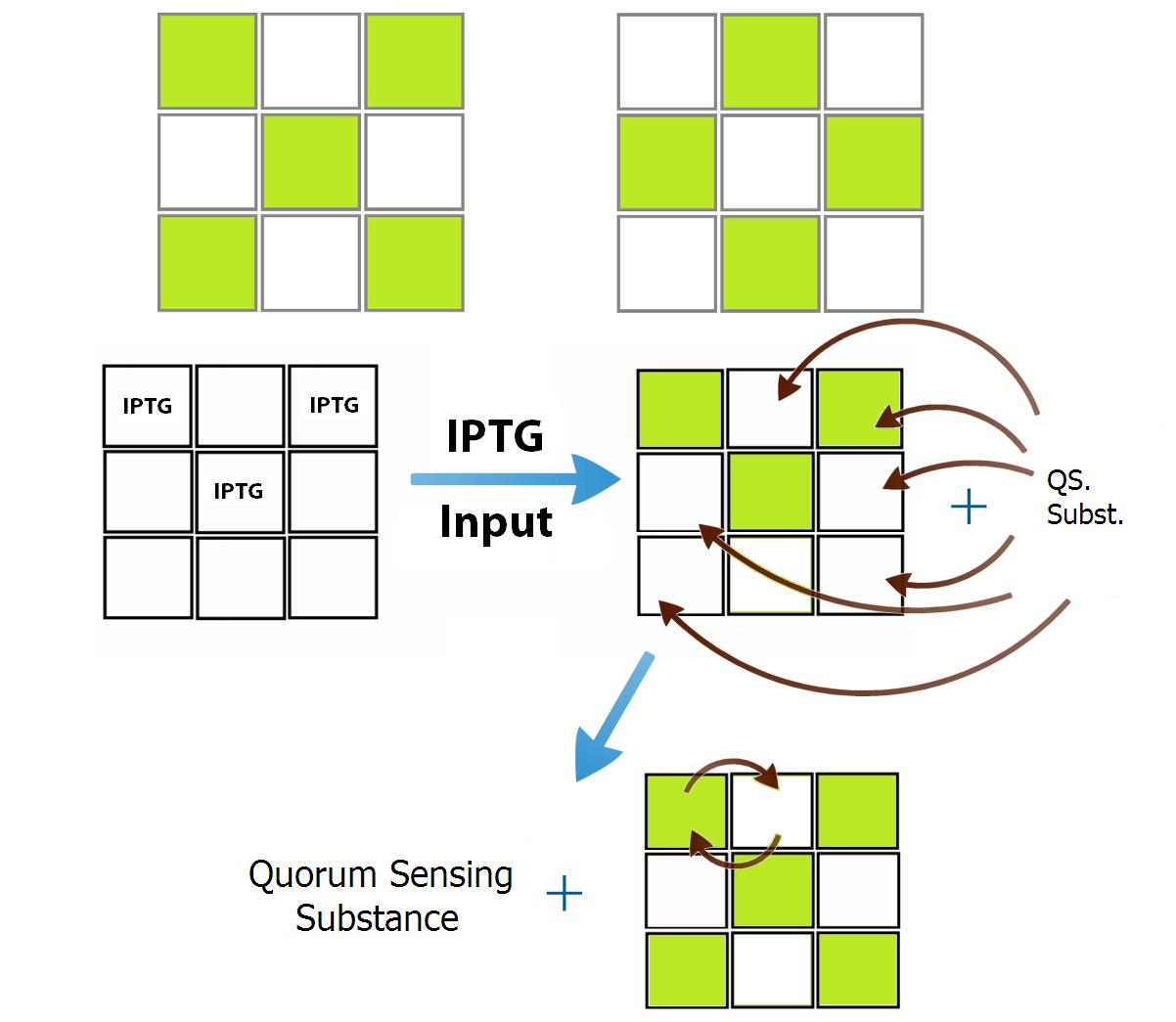
Despite the solution we found to the specificity of the communication, another problem appears when we try to genetically build the bacterial populations: there are not enough quorum sensing systems to create 9 bacterial populations. In the Registry of Parts there are 4 quorum sensing systems well characterized, and there is a strong activation crosstalk between two of them (Las and Rhl), this fact prevent us from using them, therefore, we end up with 3 systems of quorum sensing that can be used. As a proof of concept we design two populations of bacteria that comunicate between them repressively. Because of this limitation we chose the patterns "X" and "O" in our 9 wells device. In this case, because of the simmetry of the positions, only two different population of bacteria are need. In these patterns there is no intersection between "letter X" and letter"O”, which greatly simplifies the configuration of communication weights between positions (see Figure 5). Because each position of the “X” inhibits all positions of “O” and activates all positions of its own pattern (and vise-versa), there is no need to distinguish between the kind of signal (quorum sense substance) that each position of the “X” emits. The same works for all positions of the “O” pattern. Still, the positions of each pattern can be programmed with the same genetic code, which allow us to use only two systems of quorum sensing to create a network of associative memory that is capable of differentiate between two memories, given a particular input that would be interpreted as an incomplete memory.
We decided to use two of the four available quorum sensing systems that have substances different enough for the bacterial communication so there would be little cross-talk between them. The quorum sensing systems chosen were Cin and Rhl.
The training of the network is previously defined in silico and it is inserted in the bacteria through a genetic construction. Each population of bacteria ("neuron") needs his own QSM and because of that the number of "neurons" is limitated to the number of QSMs. As a proof of concept we design two populations of bacteria that comunicate between them repressively. Because of this limitation we chose the patterns "X" and "O" in our 3x3 wells device. In this case there are need only two different population of bacteria since the system is simmetric.
To convert the signals in activation or inhibition, we created a system of transduction of the quorum sensing signal to transcription of an activator or an inhibitor of the transcription of GFP, this will be our system activation reporter. Simultaneous inhibitions and activations of a bacterial population will be converted to a molecular competition of activators and inhibitors by the promoter that controls the production of GFP. It is this molecular competition that promotes the decision between the memories of the communication systems, associating a given input with a more similar memory. As an example, if an input activates more positions of the “X” pattern than the “O”, the competition in the pattern “X” positions will be more favorable to its activation due to the greater number of activators produced by the activated positions, while in the positions of the “O” pattern the opposite occurs, because of its small number of positions activated initially by the given input.
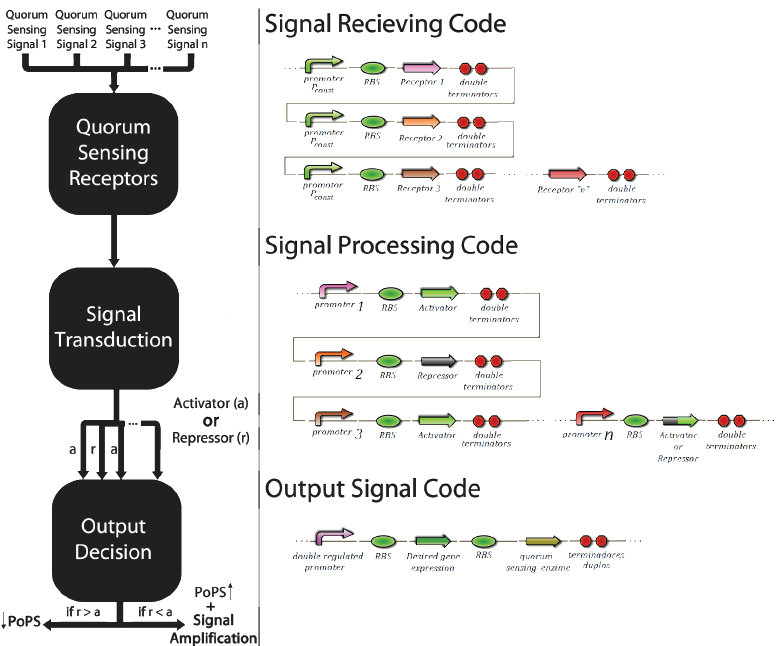
The promoter multi-regulated by an activator and an inhibitor is called Prm. Its inhibitor is the transcriptional factor cl434 and its activator is the cl factor. The genetic design of the positions of the patterns “X” and “O” can be seen in Figure 6.
The construction using the signal transduction containing cl434 and cl allows creating different systems of associative memory, limited only by the quantity of quorum sensingsystems available. Figure 6 shows how this generic system would work and elucidates how this system could be applied to different functions involving a genetic control.
 "
"