Team:USTC-China/results
From 2012.igem.org
(Difference between revisions)
| Line 101: | Line 101: | ||
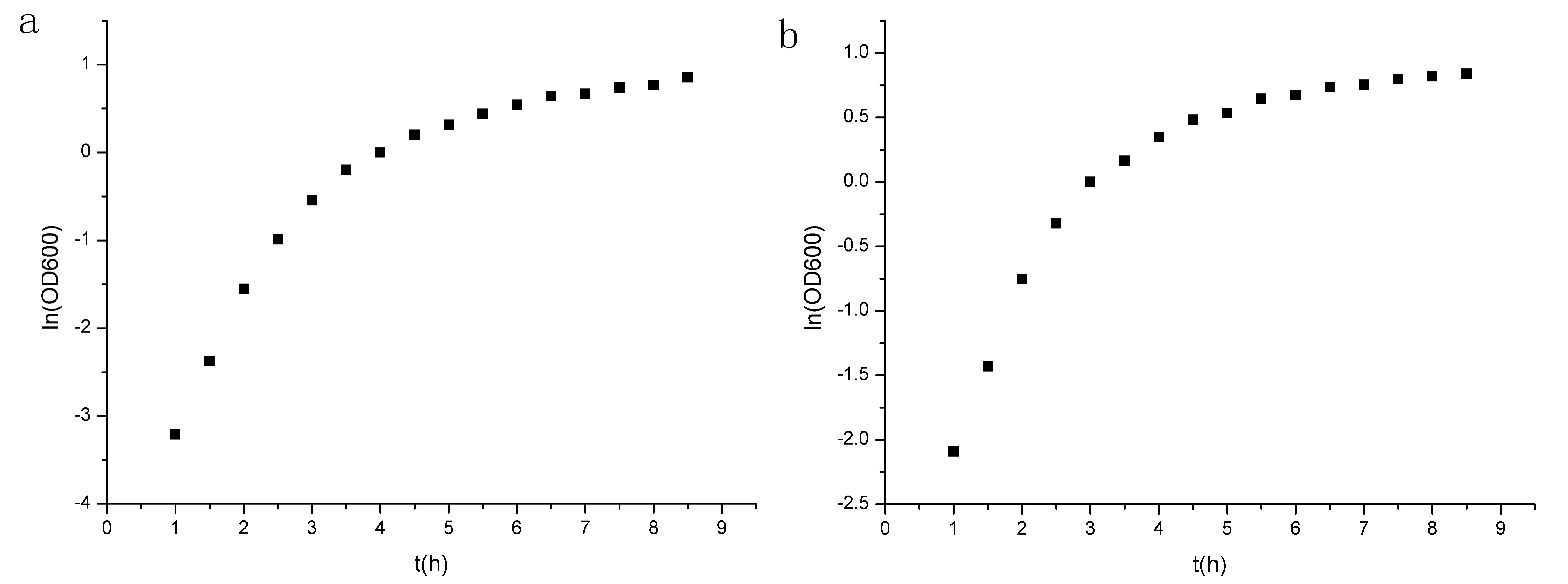
<p>x is the concentration of microbe.x0 is the initial concentration when t=t0.μm is the natural growth rate.</p> | <p>x is the concentration of microbe.x0 is the initial concentration when t=t0.μm is the natural growth rate.</p> | ||
<p>Calculate the natural logarithm of both side of the equation,we can get:</p> | <p>Calculate the natural logarithm of both side of the equation,we can get:</p> | ||
| - | + | ||
<div align="left" style="width:280px;height:auto;margin-left:200px;"> | <div align="left" style="width:280px;height:auto;margin-left:200px;"> | ||
<a href="https://static.igem.org/mediawiki/2012/3/30/Formulaustc2.jpg"><img src="https://static.igem.org/mediawiki/2012/3/30/Formulaustc2.jpg" alt="Curve" style="clear:both;width:280;height:49px;"></a></div> | <a href="https://static.igem.org/mediawiki/2012/3/30/Formulaustc2.jpg"><img src="https://static.igem.org/mediawiki/2012/3/30/Formulaustc2.jpg" alt="Curve" style="clear:both;width:280;height:49px;"></a></div> | ||
| - | <p>linear to the variable t.And the slope is μm.</p> | + | <p>Obviously,the variable lnx is linear to the variable t.And the slope is μm.</p> |
<p>We calculate the natural logarithm of OD600 data we get and do linear fit to the data.Then we get the slope which is the natural growth rate μm.</p> | <p>We calculate the natural logarithm of OD600 data we get and do linear fit to the data.Then we get the slope which is the natural growth rate μm.</p> | ||
<p>We assume that μm can reflect the rate of cells death caused by the basic expression of lysis.If the death effect can't be ignored,the value of μm obtained from the experimental group will be obviously less than the control group.</p> | <p>We assume that μm can reflect the rate of cells death caused by the basic expression of lysis.If the death effect can't be ignored,the value of μm obtained from the experimental group will be obviously less than the control group.</p> | ||
Revision as of 13:22, 25 September 2012
RESULTS
 "
"