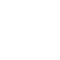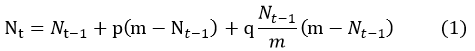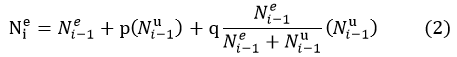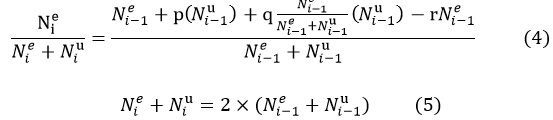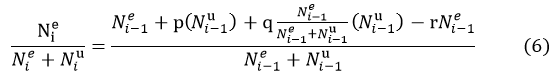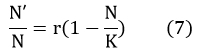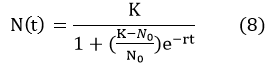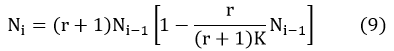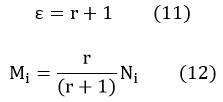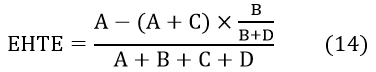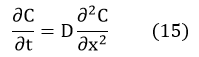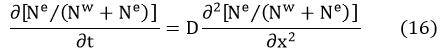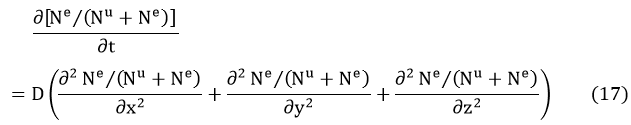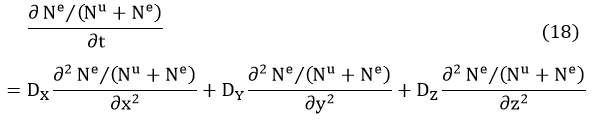Team:Tianjin/Modeling/HGTBass
From 2012.igem.org
(→The Effects of Parameters on the Shape of the Curve) |
(→Real Condition) |
||
| Line 229: | Line 229: | ||
After such simplification, the equation (9) can be expressed in equation (13). | After such simplification, the equation (9) can be expressed in equation (13). | ||
[[File:TJU2012-Mode-HGT-equ-12.png|center|equation13]] | [[File:TJU2012-Mode-HGT-equ-12.png|center|equation13]] | ||
| - | We have simulate the changing number of the E and W bacteria and the total number of bacteria through MATLAB program. The simulation result are shown in '''Fig. | + | We have simulate the changing number of the E and W bacteria and the total number of bacteria through MATLAB program. The simulation result are shown in '''Fig. 6'''. |
| - | [[file:TJU2012-Mode-HGT-fig-5.png|thumb|500px|center|'''Figure | + | [[file:TJU2012-Mode-HGT-fig-5.png|thumb|500px|center|'''Figure 6.''']] |
We can also see that there are some differences between the curves of ideal condition and the real condition, we can see that the difference is result from the environmental constraints. | We can also see that there are some differences between the curves of ideal condition and the real condition, we can see that the difference is result from the environmental constraints. | ||
| - | [[file:TJU2012-Mode-HGT-fig-6.png|thumb|500px|center|'''Figure | + | [[file:TJU2012-Mode-HGT-fig-6.png|thumb|500px|center|'''Figure 7.''']] |
=Model Extension 1: the Transgression≠Expression= | =Model Extension 1: the Transgression≠Expression= | ||
Revision as of 08:20, 25 September 2012

Background
Genetic pollution is the term of genetics in which the genetic information is transferred in to the organisms where it is not needed or where this information never existed before. This flow of genetic information is usually undesired and cannot be controlled. The flow of genetic information usually takes place between the genetically modified organisms into the organisms which are not genetically modified.
Unlike other forms of pollution, genetic contamination has the potential to be a problem that multiplies as plants and microorganisms grow and reproduce. Therefore, environmental damage caused by genetically modified organisms (GMOs) cannot be confined to the original habitat. This briefing considers what is known about these risks and the evidence that is emerging from experimental and commercial growing of GE crops.
Horizontal gene transfer (HGT), also lateral gene transfer (LGT) or transposition refers to the transfer of genetic material between organisms other than vertical gene transfer.
HGT is the primary reason for bacterial antibiotic resistance. Genes that are responsible for antibiotic resistance in one species of bacteria can be transferred to another species of bacteria, subsequently arming the antibiotic resistant genes' recipient against antibiotics.
Due to the increasing amount of evidence suggesting the importance of these phenomena for evolution molecular biologists such as Peter Gogarten have described HGT as "A New Paradigm for Biology".
Our Problem
There are two ways for wild type bacteria to have some exogenous gene. To make it more convenient to distinguish between the two type of bacteria, we call the bacteria containing exogenous gene the E bacteria. Similarly, the wild type bacteria are called the W ones. We want to study how the exogenous gene horizontally transferred from to other bacteria and how the number of W bacteria and E bacteria changed with time.
Our Experiment Design
We studied the how the number of E. bacteria increased with mutation and HGT. This is an important reason for the genetic pollution.
In our experiment, we have cultivated some W bacteria in the substrate whose initial number is N0w. At the same time, we induce E bacteria, the same bacteria as the W ones but contains the exogenous gene on their plasmid. The initial number of the evil bacteria is N0e.
We will test the number of E and W bacteria every other ∆t, while ∆t is the generation time. We assume the generation time of the W and E bacteria are identical because they belong to the same species.
Model Inspiration: Bass Diffusion Model
The Bass diffusion model was developed by Frank Bass and describes the process of how new products get adopted as an interaction between users and potential users. Mathematically, the basic Bass diffusion is a Riccati equation with constant coefficients. This model has been widely influential in marketing and management science. What is more, the mathematic concept has also inspired me. Before our description of our model, we had better get to know the details of the Bass model. The formula of our model is listed as equation (1).
In equation (1), the Nt represents the number of consumers who have purchased the product when time is t, represents the total number of consumers and potential consumers, p is the coefficient of innovation which stands for the degree of how the consumers tend to try new things. While q is the coefficient of imitation which stands for the degree of how the consumers tend to be imitate other people who are trying the products.
This is the Bass model that inspired us about how the gene transfer horizontally.
Rudimentary Model
The rudimentary version model is extraordinarily similar to the Bass model in equation (2), but the meaning of all the parameters and coefficient.
In the equation, Nie stands for the number of E bacteria at the time=i×∆t. Niw stands for that of the wild type bacteria. However, in this model, the coefficient p and q has very different meaning. The coefficient p stands for the probability of the exogenous gene resulting from the mutation; and the coefficient q stands for the probability of the exogenous gene resulting from the HGT. The interval is the generation time of the bacteria.
In this rudimentary model, we assume the total number of E and W bacteria is constant. The number of E bacteria increased is only due to the HGT and the gene mutations. To be more specific, the number of increased is proportional to that of the percent of E bacteria and the number of W ones. The diagram is shown in Fig. 1.
The Effects of Parameters on the Shape of the Curve
In order to study how the parameters impact the shape of the curve, we changed the two important parameters p and q in the formula, and also compared the shapes of the curves under different conditions.
First of all, we studied how the increasing of p impacts the shape of the curve. The diagram of curves at the three different p is shown in Fig. 2.
It is not difficult to conclude that the number of E bacteria will increase much faster when the parameter p increased. So the mutagenesis will increase the speed of the percentage of E. bacteria.
After that, we studied how the increasing of q impacts the shape of the curve. The diagram of curves at the three different q is shown in Fig. 3.
It is easy to conclude that the number of E bacteria will increase much faster when the parameter q increased. So the other method to increase the probability of HGT will increase the increasing speed of the percentage of E. bacteria.
Final Model
There are still some problems exist in the rudimentary version of our model, for example the number of E b and W bacteria remains constant in the rudimentary version. What is more, the plasmid may get lost during the growth of the bacteria. If all these factors are taken into our consideration, the model can be more convincing.
As for the correction term of plasmid loss, we assume it is proportional to that of the number of E bacteria. Thus, the formula can be rewritten as the equation (3)
Furthermore, we had better study how the number of bacteria change with the time.
We assume the interval is exactly the generation time of the bacteria. We also assume the generation time of the E bacteria is the same as that of the W bacteria.
How the number of bacteria change with the time? If these bacteria are cultivated under the ideal condition, there is no limitation of the nutrition or other living conditions. As a result, the bacteria can grow in an ideal speed. However, if the living conditions are limited to the bacteria, the number of bacteria is a little complicated. Consequently, the discussion of this problem should be based on a case by case analysis.
Ideal Condition
As mentioned before, if the bacteria are cultivated under ideal condition, the number changed is directly related to the bacteria themselves. To make it simple, we assume the bacteria is multiplied by binary fission; then the number of bacteria changed can be expressed in equation (4) and (5).
The number of total bacteria will increase with the time exponentially and the following figure described the relationship between time and bacteria number.
Real Condition
If the bacteria are cultivated in a limited living condition, there will be a certain population bearing capacity. However, the percentage of the E and W bacteria will not be affected by the change of total number.
Thus the change of the two bacteria can be expressed in the following equation (6).
The changing rule of the total bacteria number is complicated. There is a famous logistic trait model which can express the rule of our system. The model can be expressed in equation (7).
In the formula, the N represents the total number of the two bacteria; the K represents the maximum number of bacteria number under our experimental condition.
Through separation of variables, we can solve this equation. The solution of our equation is listed in the equation (8).
We assume the total number of the two bacteria at t=0 is N0.
However, in the previous description of our model, we use discrete time to describe the time. So, we also dispersed the time in equation (8) to express the rule, which is listed in equation (9).
In this equation, the Ni means the number of total bacteria.
To simplify the equation, we have the following equations.
After such simplification, the equation (9) can be expressed in equation (13).
We have simulate the changing number of the E and W bacteria and the total number of bacteria through MATLAB program. The simulation result are shown in Fig. 6.
We can also see that there are some differences between the curves of ideal condition and the real condition, we can see that the difference is result from the environmental constraints.
Model Extension 1: the Transgression≠Expression
The HGT parameter q is a little bit complicated to evaluate because not all the horizontally transferred gene can express successfully. To evaluate the general gene transfer and expressed level, we also create a novel method to evaluate the HGT level with the help of an evaluation index EHTE (effect of horizontal transgression and expression).
In our experimental strategy, the exogenous gene is on a plasmid in the bacteria. We also designed another label on the same plasmid. Consequently, we can measure the number of bacteria transferred and the bacteria whose transferred gene expressed successfully.
The definition of the evaluation index EHTE is expressed in the following equation (14).
In the formula, A, B, C and D have the following meanings.
- A means the number of bacteria to whom the plasmid have been horizontally transferred and the bad gene on the plasmid have been successfully expressed.
- B means the number of bacteria whose bad gene come from the mutation.
- C means the number of bacteria who have been horizontally transferred but the bad gene on the plasmid have not been successfully expressed.
- D means the bacteria who have not been horizontally transferred and do not have such bad gene from mutation.
Model Extension 2: the Spatial Description of Gene Transference
In the previous model, we have described the change of the two kinds of bacteria number dependent on time. However, to make our project more comprehensive, we need to study how the exogenous gene spread across the space. In this study, we have designed a model to describe how the gene transferred in the two dimensional plate.
The general rules that control the diffusion of all things are similar, and the most famous diffusion equation that can describe the general diffusion is the Fick's Law. Of course, HGT through the space can also be expressed by the diffusion equation (15).
When we use such general equation in the field of gene diffusion, the general gene diffusion equation can also be paraphrase in the equation (16).
In the equation, the Nw means the number of the W bacteria, Ne means the number of E bacteria; t represents the time of diffusion, x means the length of diffusion.
If we consider the three dimensional diffusion, the equation should be expressed in equation (17).
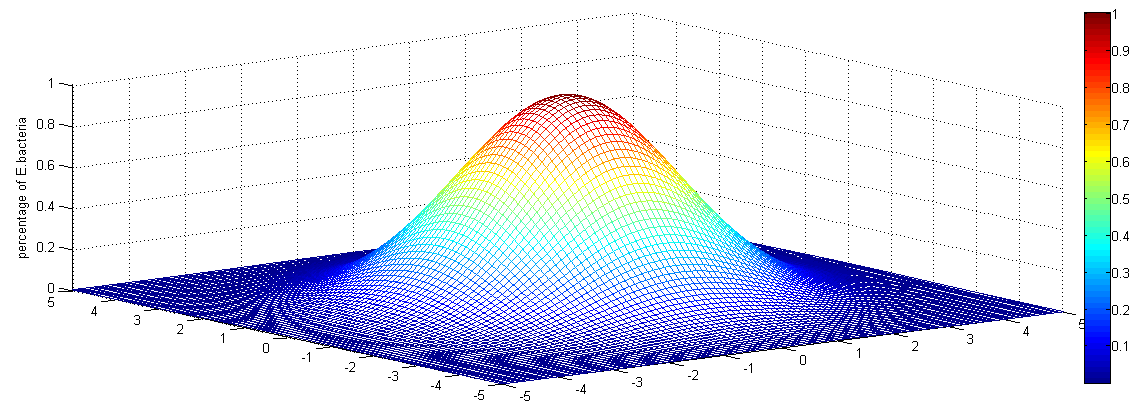
The HGT through a two dimensional plate are shown in Fig. 7.
If we also consider the anisotropy of diffusion in different directions, the equation can also be specified as equation (18).
And the figure through a two dimensional plate are shown in Fig. 8.
Future Work
In the meantime, our experiments are still ongoing. The preliminary experimental results correspond with our modeling. We are about to achieve more relative parameters. In this way, we can analyze divergence between our model and real situation. This divergence will serve to guide us in the further optimization of our model.
We can devise the experimental design to measure the coefficient p, q and r. The parameter r is directly related that of the property of plasmid and the chassis. The mutation coefficient p is very minute; it should be directly related to the outside condition, if there are some mutagens or some other mutation condition such as UV treatment.
What is more, if the generation time of the evil bacteria is different from that of the uncontaminated ones. We can also consider this issue into our consideration, to use ordinary differential equation to express such changing rule of bacteria.
To make it more complicated, we can also consider the problems with many plasmids or more than one bad gene. Thus, the evaluation index EHTE and the equation of the changing number can also be different.
 "
"