Team:Amsterdam/modeling/generaldesign
From 2012.igem.org
(→In practice) |
(→Model definition) |
||
| Line 132: | Line 132: | ||
is always true in the model, the total amount of plasmids has also been plotted (purple). This clearly shows the limiting value of the plasmid population count, specified by the capacity limit (<math>Ca</math>). This is reached around <math>t=10</math> with the parameter set used here. | is always true in the model, the total amount of plasmids has also been plotted (purple). This clearly shows the limiting value of the plasmid population count, specified by the capacity limit (<math>Ca</math>). This is reached around <math>t=10</math> with the parameter set used here. | ||
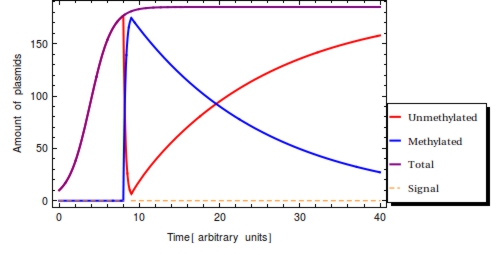
| - | + | [[File:Timelapse.jpg|frame|center|Time simulation of the system of ODE’s. Input signal <math>S(t)</math> with <math>s_{\text{on}} = 3</math> and <math>s_{{\text{off}}} = 4</math>. Detection of the signal converts all <math>P_{0}</math> (red) to <math>P_{1}</math> (blue) on a short time scale. After the amount <math>P_{1}</math> will start to diminish due to cell division. Eventually, the steady state will be restored once again and the cell’s capacity for plasmids will be completely taken up by <math>P_{0}</math> plasmids.]] | |
| - | [[File:Timelapse.jpg| | + | |
| - | + | ||
| - | + | ||
Unknown variables affecting <math>F(t)</math> in a real-life setting would be the time of signal onset, signal duration and signal strength. Knowing the values for two of these three values, the value of the third can be solved for. Here we will simply assume maximal signal strength during <math>s_{\text{on}}</math> and <math>s_{\text{off}}</math>. | Unknown variables affecting <math>F(t)</math> in a real-life setting would be the time of signal onset, signal duration and signal strength. Knowing the values for two of these three values, the value of the third can be solved for. Here we will simply assume maximal signal strength during <math>s_{\text{on}}</math> and <math>s_{\text{off}}</math>. | ||
Revision as of 11:33, 23 September 2012




Contents |
Introduction
The molecular design in a nutshell
We’ve established in a very early stage of the design process that we were going to use DNA methylation as the molecular mechanism to create our storage mechanism. DNA methylation, which means enriching of a specific nucleotide with a methyl group, is performed by a group of proteins called the methyltransferases. In choosing DNA-methylation as the foundation of our storage mechanism, we were heavily influenced by the DamID technology which has been originated by Bas van Steensel (van Steensel and Henikoff 2000; van Steensel, Delrow, and Henikoff 2001). By fusing a bacterial methyltransferase (MTase) to a eukaryotic transcription factor of which van Steensel wanted to find out where it binds on the genome, he was able to infer the transcription factor binding sites on the eukaryotic genome by reading out which regions were methylated.
We thought we could reverse this idea to create a memory unit, at the core constituted by an MTase that would methylate an especially designated genomic region but only in reaction to the sensing of a signal by the cell. The epigenetic status of the bit region could thus either be 1 (methylated/written) or 0 (ummethylated/unwritten), effectively forming a binary memory unit.
Finally, the methylation status of the bit region can be assessed using digestion of the plasmid extracts with the MTase-coupled RE, followed by analyzing the band lengths intensities of a gel electrophoresis of the product. This final read-out step is covered more in depth in section [sub:gelinfer]
Choosing a methyltransferase
To create this system, we first required an MTase that: i) is not already present in the chassis organism E.coli, ii) has a binding motif of that is not methylated by any other MTases in the system and iii) for which a restriction enzyme (RE) dependent upon the action of this methyltransferase has been identified. This last condition is always true for any methyltransferase which has been identified to be part of a bacterial [http://en.wikipedia.org/wiki/Restriction_modification_system Restriction/Modification system]. We wrote a python script to mine the [http://rebase.neb.com/rebase/rebase.html REBASE] database of REs and MTases for a MTase that meets our needs. We found an ideal candidate: M.ScaI, originally from Streptomyces caespitosus. The only remaining design question was how to control the activity of the fusion protein as we would want it to only be active in the presence of the generic signal. This design question will be more elaborately discussed in the next section.
Extending the idea to multiple bits
Extending the design idea further, we realized that it should be possible to register and store the presence of multiple signals smultaneously in a single cell. By fusing DNA binding proteins to the methyltransferase and adding their corresponding DNA binding motifs to the bit regions of the DNA. Either traditional bacterial transcriptional regulators could be used for this purpose or the Zinc-Finger Array (ZFA) technology <ref>Fu, Fengli, Jeffry D. Sander, Morgan Maeder, Stacey Thibodeau-Beganny, J. Keith Joung, Drena Dobbs, Leslie Miller, and Daniel F. Voytas. 2009. “Zinc Finger Database (ZiFDB): a repository for information on C2H2 zinc fingers and engineered zinc-finger arrays.” Nucleic acids research 37 (jan): 279. doi:10.1093/nar/gkn606. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2686427\&tool=pmcentrez\&rendertype=abstract</ref>. ZFA allows the construction of highly specific artificial protein-DNA interactions (Kaseniit, Perli, and Lu 2011). By fusing the MTase to a Zinc Finger or traditional transcriptional regulator and extending the bit region with the transcriptional regulator’s binding motif, the binding affinity of the fusion protein for the DNA motif could increase about 18-fold (McNamara et al. 2002) (A C5-cytosine MTase was studied here, not in the class of N4C-MTases to which M.ScaI belongs). This will heavily diminish the possible aspecific cross-talk between FPs and bits assigned to other FPs. The same MTase could then be used for different signals with a very low chance of cross-talk between FPs and other signals’ bits.
Part more specific on read out, unique band lengths
Inferring the time of signal onset
Methylated bits over time
Numerous copies of identical plasmids are often present in single cells and plasmids replicate independently of the bacterial chromosome (Scott 1984). A plasmid copy number (PCN) has been determined for all plasmids in the Parts Registry, which indicates a likely amount of copies of the plasmid to be present in each cell. Unlike eukaryotes, prokaryotes do not copy DNA methylation patterns to the newly synthesized strand during DNA replication. This will lead to a dilution of the amount of ‘written’-plasmids over time, mostly due to cell replication and the ensuing binomial division of the plasmids in the parent cell among the two daughter cells.
The volatility of this memory design seemed like a downside at first, but quickly opened our eyes to a very exciting feature of this system. By analyzing the fraction:
<math>F(t) = \frac{\text{written plasmids}}{\text{written + unwritten plasmids}}</math>
at the time of memory read-out, the time at which the signal was registered by can be inferred.
Using the here presented model, we will examine how this inferrance of signal detection time can be performed. Another goal of this model is to gain insight into the effects of the various parameters (e.g. plasmid replication and degradation rate) on <math>F(t)</math>. As this model has the sole purpose of clarifying the desired system behaviour, it is okay for units in this model to be dimensionless.
Model definition
First, let’s model the input signal/compound which is to be reported on. Imagine the to be stationary and positioned along a fluidic stream so that the signal to be registered can pass the. Modelling the signal using the piecewise function <math>S(t)</math> now seems appropriate. Here, <math>s_{\text{on}}</math> is defined as the time at which the signal is first encountered and <math>s_{\text{off}}</math> as the time at which the signal is turned off.
<math> S(t) = \begin{cases}
0 & \text{ if } 0 \le t \le s_{\text{on}} \cr
1 & \text{ if } s_{\text{on}} \le t \le s_{\text{off}} \cr
0 & \text{ if } s_{\text{off}} \le t \le \infty
\end{cases} </math>
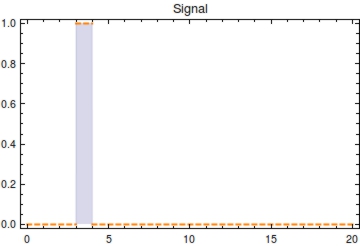
Figure 1. Plot of the input signal <math>S(t)</math> with <math>s_{\text{on}}</math> at 3 and <math>s_{{\text{off}}}</math> at 4
We will model a single cell with multiple identical plasmids. Each of the plasmid copies contain the gene for the methyltransferase and the so called bit region, which is the region especially purposed to be methylated in presence of a signal. The following assumptions/conditions are made:
- A well stirred cellular system with no spatial concentrations differences and all species' concentrations large enough to be approximated by continuous functions. Hence we will use a set of ordinary differential equations (ODE’s)
- To ease the analysis of the model, a single unique bit with multiple copies per cell is considered here
- <math>P_{0}</math> denote plasmids that have the single bit set to 0, no write event has taken place in these cells
- <math>P_{1}</math> denote plasmids in which the bit has been flipped to 1 in response to encountering the signalling compound
- <math>P_{\text{T}}</math> denotes the total amount of cells in the sytem, <math>P_{0} + P_{1}</math>
- Assumed is a high response rate (3 min) termed <math>\omega</math>, which is the constant rate with which the system responds with methylation of the bit region to the detection of the signal.
- Logistic growth for the plasmid population inside the cell, with a capacity limit of <math>Ca = 40</math>, the copy number of a low copy number plasmid.
- Alternatively, this maximal plasmid number could also be described as the fraction between the plasmid proliferation rate (<math>\beta</math>) and degradation rate (<math>\alpha</math>). The steady state amount of plasmids in the cell will be determined by <math>P_{\text{SS}} = \frac{\beta}{\alpha}</math>, the solution to the differential equation <math>P'(t) = \beta P - \alpha P</math>.
- Accumulation of cells in which the bit has been written is assumed to result in non-written cells; methylation patterns are not copied to the progeny in prokaryotes.
From these rules, the following system of ODE’s has been constructed: $$ \begin{aligned} \frac{dP_{0}}{dt} &=& k\ P_{0+1}\ (1 - \frac{P_{0+1}}{\text{Ca}}) - \omega\ S(t)\ P_{0} - \alpha\ P_{0} \\ \frac{dP_{1}}{dt} &=& \omega\ S(t)\ P_{0} - \alpha\ P_{1} \end{aligned} $$
Table 1: Parameter values for the plasmid methylation model
| Parameter | Value |
|---|---|
| k | 0.8 |
| <math>\alpha</math> | .06 |
| Ca | 200 |
| <math>\omega</math> | 4 |
Table 2: Initial species values for the plasmid methylation model
| Species | Value |
| <math>P_{0}(0)</math> | 10 |
| <math>P_{1}(0)</math> | 0 |
Using the parameter values of Table 1 a simulation with a duration of 40 time units is shown in Figure 2. The plasmid population within a Cellular Logbook is shown to be completely converted to methylated plasmids shortly after <math>s_{\text{on}}</math>. As long as the signal is still present – until <math>s_{\text{off}}</math>, – the bit on all newly copied plasmids will be immediately methylated as the signal is still present. After <math>s_{\text{off}}</math>, <math>F(t)</math> will start to decrease. This is mostly due to cell division, during which the cell’s plasmids will be binomially distributed between the two two daughter cells, halving the plasmid amount every division cycle. In this simulation, this degradation due to cell division has been accounted for in the constant degradation rate <math>\alpha</math>. The duration of time after which a small trail of methylated plasmids is still present is related to two factors: positively to the amount of methylated cells at <math>s_{\text{off}}</math> and negatively to the plasmid degradation rate.
To reinforce that: $$ P_{0} + P_{1} = P_{\text{T}} \le \text{Ca} $$ is always true in the model, the total amount of plasmids has also been plotted (purple). This clearly shows the limiting value of the plasmid population count, specified by the capacity limit (<math>Ca</math>). This is reached around <math>t=10</math> with the parameter set used here.
Unknown variables affecting <math>F(t)</math> in a real-life setting would be the time of signal onset, signal duration and signal strength. Knowing the values for two of these three values, the value of the third can be solved for. Here we will simply assume maximal signal strength during <math>s_{\text{on}}</math> and <math>s_{\text{off}}</math>.
The response rate <math>\omega</math> of the Cellular Logbook could limit <math>F(t)</math>, as a low <math>\omega</math> might yield incomplete methylation of all plasmids before <math>s_{\text{off}}</math>. This rate should be experimentally determinable before actual deployment and application of our system and is more closely looked at in the next section. It is likely to be several magnitudes greater than the cellular division rate, however. Every single gene on a plasmid is thus expected to be methylated within at most 5 minutes of registering of the signal.
Assuming that the plasmid population will have reached its stationary state level before is plausible and eases the analysis somewhat. If the capacity limit has not been reached yet before, a lower value of results than had the capacity limit been reached. This could fool an experimentalist into thinking that the signal was detected relatively long ago, when in fact the amount of plasmids was still very low at <math>s_{\text{on}}</math>, such that total plasmid population <math>P_{\text{T}}</math> has continued to expand since <math>s_{\text{on}}</math>.
In theory
The monotonically decreasing value of <math>F(t) = \frac{\text{methylated plasmids}}{\text{total plasmids}}</math> can be used to infer <math>s_{\text{off}}</math>, given that the degradation rate (<math>\alpha</math>) and capacity constraint <math>Ca</math> are known and constant. Also assumed is that all bits are methylated during signal presence, this implicates <math>\omega</math> is sufficient to methylate all bits during presence of the signal. Irrespective of the initial amount of plasmids, the population of plasmids within the single cell will have reached a steady state value of <math>\frac{\beta}{\alpha}</math>. As we see in the Figure 2, <math>F(t)</math> will start to decrease as a function of the degradation rate after the signal has left the medium following the following function:
<math>\frac{dP_{1}}{dt} = - \alpha\ P_{1}</math>
Integrating this differential equation, <math>P_{1}</math> will be given by:
<math>P_{1}(t) = F(t) = e^{-\alpha t}</math>
Multiplying <math>F(t)</math> by the steady value <math>\frac{\beta}{\alpha}</math> will yield the amount of methylated plasmids at time <math>t</math>, given that there were <math>\frac{\beta}{\alpha}</math> methylated plasmids at <math>t = 0</math>.
<math>P_{1}(t) = \frac{\beta}{\alpha} e^{-\alpha t} \label{math:Pt}</math>
By solving the previous equation, we can calculate the time <math>t</math> that has passed after <math>s_{\text{off}}</math> from <math>F(t)</math>:
<math>t = \frac{\ln(F(t))}{-\alpha}</math>
In practice

In a typical laboratory situation, doing a restriction enzyme assay on the miniprep-extracted plasmid DNA out of followed by gel electrophoresis will be the most convenient way to assess the methylation status of the bits. The relative intensities of the gel bands can then be used to infer <math>F(t)</math>, which is exemplified in Figure 3. Unmethylated bits will result in successfully digested DNA fragments and thus two bands of shorter DNA fragments. Methylated bits will not be cut and will therefore result in one longer band, shown more to the top of the gel. Thus the top and two bottom gel bands are mutually exclusive as they indicate the same (linearized) plasmid DNA to either be digested, resulting in the two bottom bands, or undigested, resulting in the top band. A high value for <math>P(t)</math> indicates recent detection of the signal, whereas a low value indicates detection to have occurred longer ago. To get a hands-on feel of the effects that the plasmid degradation and replication rate have on <math>F(t)</math>, an interactive version in Mathematica is included in the attached Mathematica file.
References
Kaseniit, Kristjan E., Samuel D. Perli, and Timothy K. Lu. 2011. “Designing extensible protein-DNA interactions for synthetic biology.” 2011 IEEE Biomedical Circuits and Systems Conference (BioCAS) (nov): 349–352. doi:10.1109/BioCAS.2011.6107799. [http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=6107799 http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=6107799].
McNamara, Andrew R., Paul J. Hurd, Alexander E. F. Smith, and Kevin G. Ford. 2002. “Characterisation of site-biased DNA methyltransferases: specificity, affinity and subsite relationships.” Nucleic acids research 30 (sep): 3818–30. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=137423\&tool=pmcentrez\&rendertype=abstract.
Scott, J. R. 1984. “Regulation of plasmid replication.” Microbiological reviews 48 (mar): 1–23. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=373000\&tool=pmcentrez\&rendertype=abstract.
van Steensel, B., J. Delrow, and S. Henikoff. 2001. “Chromatin profiling using targeted DNA adenine methyltransferase.” Nature genetics 27 (mar): 304–8. doi:10.1038/85871. [http://dx.doi.org/10.1038/85871 http://dx.doi.org/10.1038/85871].
van Steensel, B., and S. Henikoff. 2000. “Identification of in vivo DNA targets of chromatin proteins using tethered dam methyltransferase.” Nature biotechnology 18 (apr): 424–8. doi:10.1038/74487. [http://www.ncbi.nlm.nih.gov/pubmed/10748524 http://www.ncbi.nlm.nih.gov/pubmed/10748524].
 "
"