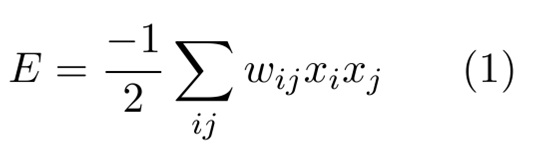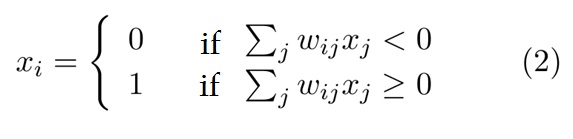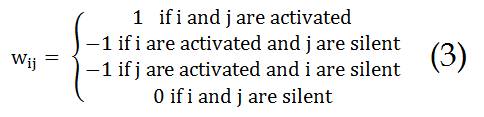"
Team:USP-UNESP-Brazil/Associative Memory/Background
From 2012.igem.org
(→Hopfield Associative Memory Networks) |
(→Hopfield Associative Memory Networks) |
||
| Line 26: | Line 26: | ||
Figure 1 shows the selection process of weights of connections between adjacent cells. To add more patterns, we have to sum the network of weights of the new pattern to the old network. (as shown in Figure 2) | Figure 1 shows the selection process of weights of connections between adjacent cells. To add more patterns, we have to sum the network of weights of the new pattern to the old network. (as shown in Figure 2) | ||
| - | [[File:009.JPG|center| | + | [[File:009.JPG|center|550px|caption|]] |
The Hopfield model for the construction of an associative memory network using bacteria is a good choice because of its simplicity and strength. The same methodology can be used to the construction of networks with other architectures, such as the “perceptrons”. One step forward is the way how to deal with continuous biological variables, because the standard model uses discrete ones. | The Hopfield model for the construction of an associative memory network using bacteria is a good choice because of its simplicity and strength. The same methodology can be used to the construction of networks with other architectures, such as the “perceptrons”. One step forward is the way how to deal with continuous biological variables, because the standard model uses discrete ones. | ||
Revision as of 15:33, 22 September 2012
IntroductionProject OverviewPlasmid Plug&PlayAssociative MemoryNetwork
ExtrasHopfield Associative Memory Networks
The main model of the project is the associative memory network made by J.J. Hopfield in the 80’s. On this model, the system tends to converge to a pre-determined equilibrium, restoring the same pattern when exposed to variations of this same pattern.
The architecture, or geometry of the system, is composed in a way that all neurons are connected .In math terms, a Hopfield Network can be represented as an “Energy” (E) function:
Where “w” values are chosen such that the stored settings are the minima of the function “E”. The variable “x” is the state of the neuron “i”.
The state of a given neuron “I”(active or silent) can be mathematically represented as follows: Given that “xi“ is the state of neuron, 1 if is activated or 0 if silent, and a neuron turns active if the sum of all received stimulus (exciting or inhibiting) is more than 0. Mathematically we can represent the state of the neuron xi as:
In this equation, “wij” is the wheight
Where "wij" is the weight assigned to the connection from neuron i to neuron j. The summation over j is the sum of all connections made by the neuron i. This dynamics (equation 2) is sufficient for the network to converge the most similar memorized pattern.
The so called “learning” of a neural network consists on the choice of “w” weights. There are several ways to choose them, what, actually, defines different learning methods
Set "i" and "j" such as the wheight "wij" is defined as:
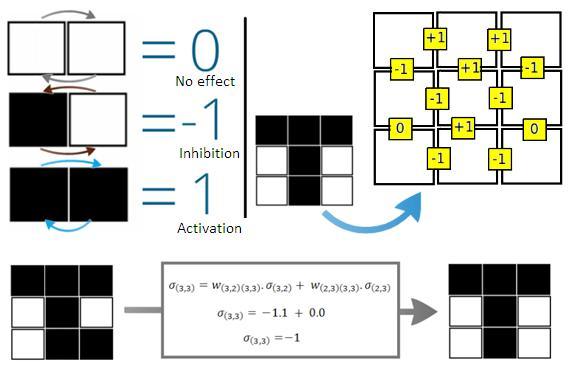
Figure 1 shows the selection process of weights of connections between adjacent cells. To add more patterns, we have to sum the network of weights of the new pattern to the old network. (as shown in Figure 2)
The Hopfield model for the construction of an associative memory network using bacteria is a good choice because of its simplicity and strength. The same methodology can be used to the construction of networks with other architectures, such as the “perceptrons”. One step forward is the way how to deal with continuous biological variables, because the standard model uses discrete ones.
