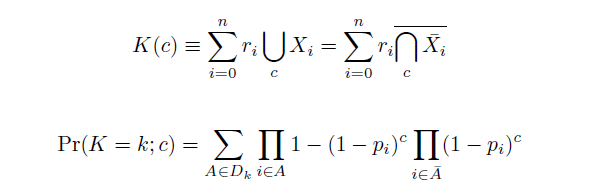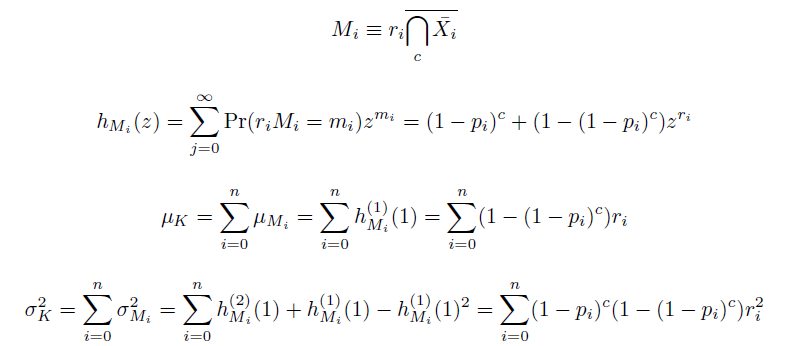Team:Yale/Modeling
From 2012.igem.org
(→Modeling the evolution of a population during MAGE) |
|||
| Line 16: | Line 16: | ||
==Modeling the evolution of a population during MAGE== | ==Modeling the evolution of a population during MAGE== | ||
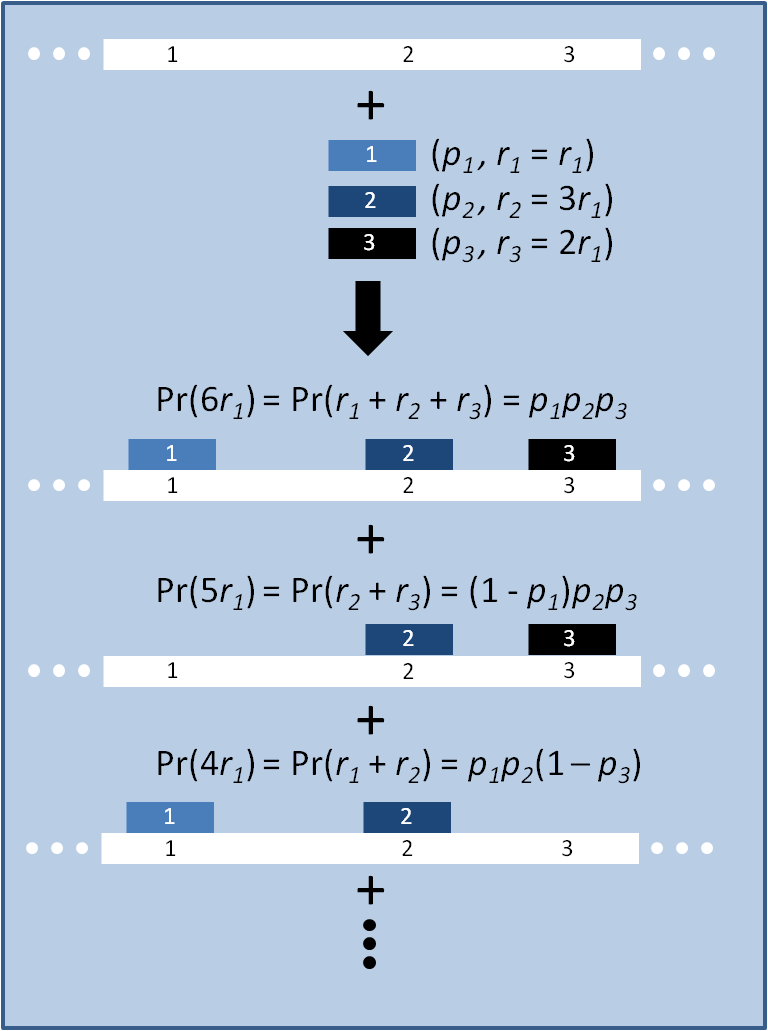
| - | [[Image:MAGE_model_scheme.png|right|300px|thumb|Figure 1. Schematic of model.]] | + | [[Image:MAGE_model_scheme.png|right|300px|thumb|Figure 1. Schematic of model. Oligos 1, 2 and 3 each carry some number of mutations ''r'' and bind their corresponding loci on the genome with probability ''p''.]] |
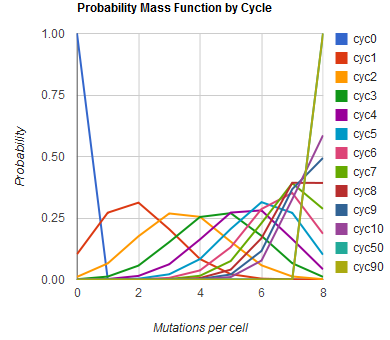
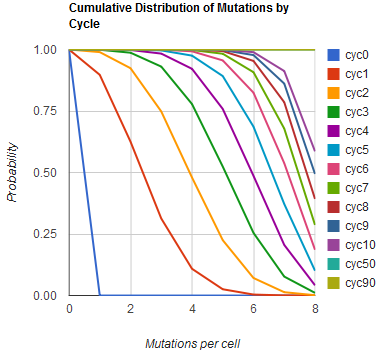
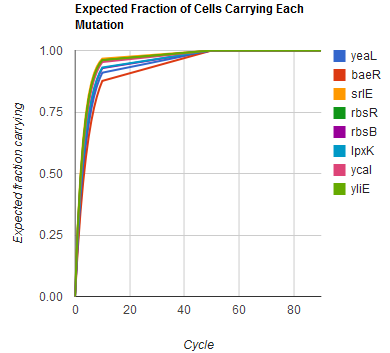
The distribution of specific mutations in MAGE is a discrete, stochastic process. How prevalent will each possible mutant be after some number of cycles? We estimate these prevalences by assuming that each oligo binds only | The distribution of specific mutations in MAGE is a discrete, stochastic process. How prevalent will each possible mutant be after some number of cycles? We estimate these prevalences by assuming that each oligo binds only | ||
Revision as of 01:22, 27 October 2012
| Home | Team | Official Team Profile | Project | Parts Submitted to the Registry | Modeling | Notebook | Safety | Attributions |
|---|
To help design MAGE experiments, both ours and others, Team Yale has developed a mathematical model of the outcomes of multiplexed recombineering, and an efficient method for its computation. A demo script is available on request.
Modeling the evolution of a population during MAGE
The distribution of specific mutations in MAGE is a discrete, stochastic process. How prevalent will each possible mutant be after some number of cycles? We estimate these prevalences by assuming that each oligo binds only
- at its target on the genome,
- completely,
- at a sequence-dependent frequency, empirically estimated for E. coli [1].
Given these assumptions, then a population after c cycles is a weighted sum of n Bernoulli trials, each zero if the oligo does not mutate its target i and otherwise equal to the number r of mutations it induces. Given efficiencies of allelic replacement p, this probability mass function becomes:
In doing this, we have derived a more general form of the binomial distribution. Computing this PMF involves solving the subset sum problem, an NP-complete problem, and so we optimized our algorithm to avoid slowdowns. In the occasional case when all oligos carry the same number of mutations, we used a recursive formula [2], and in cases not so degenerate, we used a branched, dynamic programming algorithm [3]
We also derived the moments of this distribution from its generating function.
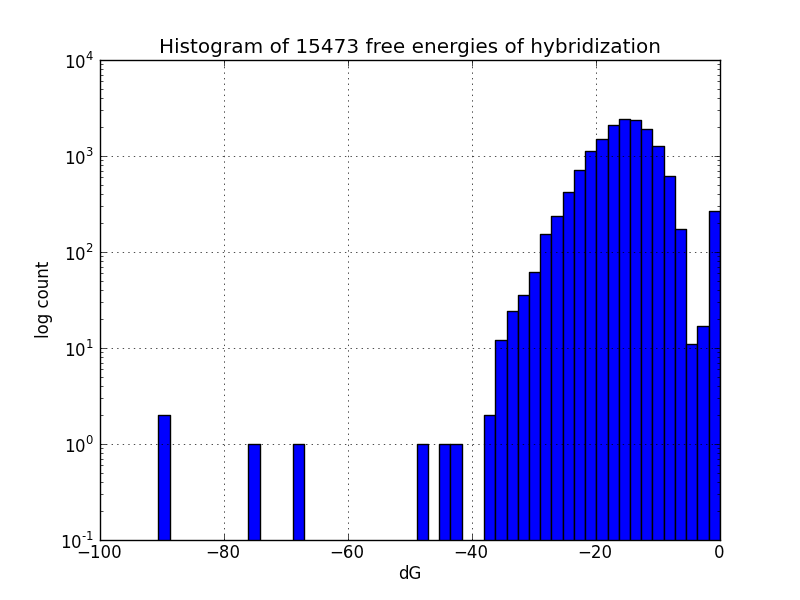
Survey for off-target binding sites
Not all MAGE-induced mutations will be at the intended sites; to identify likely unintended mutations, we scripted a search of the genome using BLAST to find subsequences with four base pairs or more matching oligos in the MAGE oligo pool, and estimates the change in Gibbs energy likely upon hybridization at each such off-target pairing, using the program UNAFold [4].
Both of these scripts have been bundled into a cloud-based tool for genomic engineering (publication forthcoming).
References
- Wang, H. H., F. J. Isaacs, et al. (2009). "Programming cells by multiplex genome engineering and accelerated evolution." Nature 460(7257): 894-898.
- Wadycki, W. J., B. K. Shah, et al. (1973). "Letters to the Editor." The American Statistician 27(3): 123-127.
- Horowitz, E. and S. Sahni (1974). "Computing Partitions with Applications to the Knapsack Problem." J. ACM 21(2): 277-292.
- Markham, N. R. and M. Zuker (2008). "UNAFold: software for nucleic acid folding and hybridization." Methods Mol Biol 453: 3-31.
 "
"