Team:Colombia/Modeling/Results
From 2012.igem.org
(→Scripting) |
(→Scripting) |
||
| Line 124: | Line 124: | ||
'''Differential equation solver''' | '''Differential equation solver''' | ||
| + | '''RALSTONIA''' | ||
| + | |||
| + | These scripts create the differential equations, find the steady state concetrations and then solve them by a 4th order Runge Kutta: | ||
---- | ---- | ||
| - | + | '''DIFFERANTIAL EQUATIONS DECLARATIONS''' | |
| - | + | ||
| + | %THIS CODE CREATE ALL THE DIFFERENTIAL EQUATIONS FOR THE SYSTEM FOR %RASTONIA | ||
function y=ecuaDifR(t,v) | function y=ecuaDifR(t,v) | ||
%---------Parameters------% | %---------Parameters------% | ||
| Line 226: | Line 229: | ||
end | end | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | '''RUNGE KUTTA''' | ||
| + | |||
| + | %FILE THAT SOLVES THE DIFFERENTIAL EQUATION AND GRAPHS THEM | ||
| + | alfS=0.9; %Basal concentration of the sensor pchS | ||
| + | alfRA=0.9; %Basal concnetration of the complez pchA-pchR | ||
| + | alfR=0.6; %Basal concentration of LuxR | ||
| + | alfI=0.4; %Basal concentration of LuxI | ||
| + | alfCI=0.5; %Basal concentration of CI | ||
| + | alfHA=1; %Basal concnetration of HipA7 | ||
| + | alfHB=0.4; %Basal concnetration of HipB | ||
| + | alfAS=0.4; %Basal concnetration of Salycilic acid | ||
| + | gammaS=1; %Degradation of Chitinase inside the cell | ||
| + | gammaRA=1; %Degradation of chitoporin | ||
| + | gammaR=1; %Degradation of LuxR | ||
| + | gammaI=1; %Degradation of LuxI | ||
| + | gammaCI=1; %Degradation of CI | ||
| + | gammaHA=1; %Degradation of HipA7 | ||
| + | gammaHB=4; %Degradation of HipB | ||
| + | gammaAS=1; %Dergradation of Salycilic acid | ||
| + | mOHS=4; %Kinetic constant for the formation of the phoshorilation of the sensor | ||
| + | mSFR=2.6; %Kinetic constant of the reaction of the phosphorilarion of the comple R | ||
| + | mA=3.5; %Kinetic constant for the activation by A | ||
| + | mIR=3; %Kinetic constant for the formation of the complex LuxILuxR | ||
| + | mI=3; %Constant that represent the union of the complex LuxILuxR with the promoter | ||
| + | mHAHB=12; %Kinetic constant for the inhibition of HipA7 | ||
| + | betaI=10; %Max production of LuxI | ||
| + | betaCI=9.96; %Max production of CI | ||
| + | betaHB=9.95; %Max production of HipB | ||
| + | betaHA=10; %Max production of HipA7 | ||
| + | betaAS=11.2; %Max production of Salicylic acid | ||
| + | kA=0.1; %Constant k of the hill ecuation for the promoter promoted by S | ||
| + | kIR=0.39; %Constant k of the hill equiation for the promorer prmoted by the complex luxIluxR | ||
| + | kCI=0.055; %Cosntant k of the hill equation for the promoter promoted by CI | ||
| + | hA=1.2; %Hill constant for the promoters promoted by S | ||
| + | hIR=3.4; %Hill constant for the promoter promoted by the complex IR | ||
| + | hCI=2.3; %Hill constant fot the promoter CI | ||
| + | eI=0.5; %Export factor of LuxI | ||
| + | jI=0.8; %Import factor of LuxI | ||
| + | deltaI=0.2;%Difusion of LuxI outside the cell | ||
| + | eAS=0.8; | ||
| + | numcel=1; %number of cells | ||
| + | %----% | ||
| + | |||
| + | h=100; %Tiempo maximo | ||
| + | |||
| + | m=0.01; %Longitud de paso [s] | ||
| + | |||
| + | t=0:m:h; %Vector tiempo | ||
| + | |||
| + | xi=[1,1,1,1,1,1,1,1,1,1,1,1]; | ||
| + | |||
| + | y=fsolve(@CondInR,xi); | ||
| + | |||
| + | conInd=y; | ||
| + | |||
| + | l=(0:m:h)'; %Vector de tiempo | ||
| + | |||
| + | x=zeros(length(l),length(conInd)); %Matriz de variables, en las columnas varia | ||
| + | %la variable y en las filas varia el tiempo | ||
| + | |||
| + | OH=zeros(1,length(l)); | ||
| + | |||
| + | x(1,:)=conInd; | ||
| + | |||
| + | for k=1:length(l)-1 | ||
| + | |||
| + | xk=x(k,:); %Captura de la ultima posicion de la matirz, es decir, los | ||
| + | %valores actuales de las variables | ||
| + | |||
| + | k1=ecuaDifR(l(k),xk); %Primera pendiente del metodo de RK4 | ||
| + | k2=ecuaDifR(l(k)+m/2,xk+(m/2*k1)'); %Segunda pendiente del metodo de RK4 | ||
| + | k3=ecuaDifR(l(k)+m/2,xk+(m/2*k2)'); %Tercera pendiente del metodo de RK4 | ||
| + | k4=ecuaDifR(l(k)+m,xk+(m*k3)'); %Cuarta pendiente del metodo de RK4 | ||
| + | |||
| + | xk1=xk+m/6*(k1+2*k2+2*k3+k4)'; %Calculo de nuevos valores para las | ||
| + | %variables | ||
| + | |||
| + | %xk1=xk+m*ecuaDif(l(k),xk)'; %Method of Newton | ||
| + | |||
| + | xk2=zeros(1,length(xk1)); | ||
| + | |||
| + | |||
| + | for p=1:length(xk1) | ||
| + | |||
| + | if(xk1(p)<0.00000001) | ||
| + | |||
| + | xk2(p)=0; | ||
| + | else | ||
| + | |||
| + | xk2(p)=xk1(p); | ||
| + | end | ||
| + | |||
| + | end | ||
| + | |||
| + | |||
| + | x(k+1,:)=xk2; %Actualizacion del nuevo vector de variables en la matriz | ||
| + | |||
| + | |||
| + | |||
| + | end | ||
| + | |||
| + | for j=1:length(l) | ||
| + | |||
| + | if (l(j)<(10) || l(j)>(20)) | ||
| + | |||
| + | OH(j)=0; | ||
| + | |||
| + | else | ||
| + | |||
| + | OH(j)=15; | ||
| + | |||
| + | |||
| + | end | ||
| + | |||
| + | |||
| + | end | ||
| + | |||
| + | S=x(:,1); | ||
| + | SF=x(:,2); | ||
| + | RA=x(:,3); | ||
| + | A=x(:,4); | ||
| + | Ii=x(:,5); | ||
| + | Io=x(:,6); | ||
| + | IR=x(:,7); | ||
| + | R=x(:,8); | ||
| + | CI=x(:,9); | ||
| + | HB=x(:,10); | ||
| + | HA=x(:,11); | ||
| + | AS=x(:,12); | ||
| + | |||
| + | figure(1) | ||
| + | plot(l,S,l,SF) | ||
| + | legend('Sensor (pchS)',' Phosporilated pchS') | ||
| + | xlabel('Time') | ||
| + | ylabel('Concetratio (micromolar)') | ||
| + | title('Response of Sensor pchS') | ||
| + | figure(5) | ||
| + | plot(l,RA,l,A) | ||
| + | legend('Complex pchR-pchA','Activator pchA') | ||
| + | xlabel('Time') | ||
| + | ylabel('Concetration (micromolar)') | ||
| + | title('Activator response') | ||
| + | figure(2) | ||
| + | plot (l,R,l,Ii,l,Io,l,IR) | ||
| + | legend('LuxR','LuxI nside the cell','LuxI outside the cell','Complex(Lux-LuxR)') | ||
| + | xlabel('Time') | ||
| + | ylabel('Concetration (micromolar)') | ||
| + | title('LuxI-LuxR system response') | ||
| + | figure(3) | ||
| + | plot (l,HA,l,HB) | ||
| + | legend('Toxin HipA7','Antitoxin HipB') | ||
| + | xlabel('Time') | ||
| + | ylabel('Concetration (micromolar)') | ||
| + | title('Toxin-Antitoxin module') | ||
| + | figure(4) | ||
| + | plot (l,OH,l,AS,l,CI) | ||
| + | legend('3-OH-PAME','Salicylic acid','CI') | ||
| + | xlabel('Time') | ||
| + | ylabel('Concetration (micromolar)') | ||
| + | title('CI and Salicylic Acid response') | ||
| + | |||
---- | ---- | ||
Revision as of 13:08, 26 September 2012
Template:Https://2012.igem.org/User:Tabima
Results
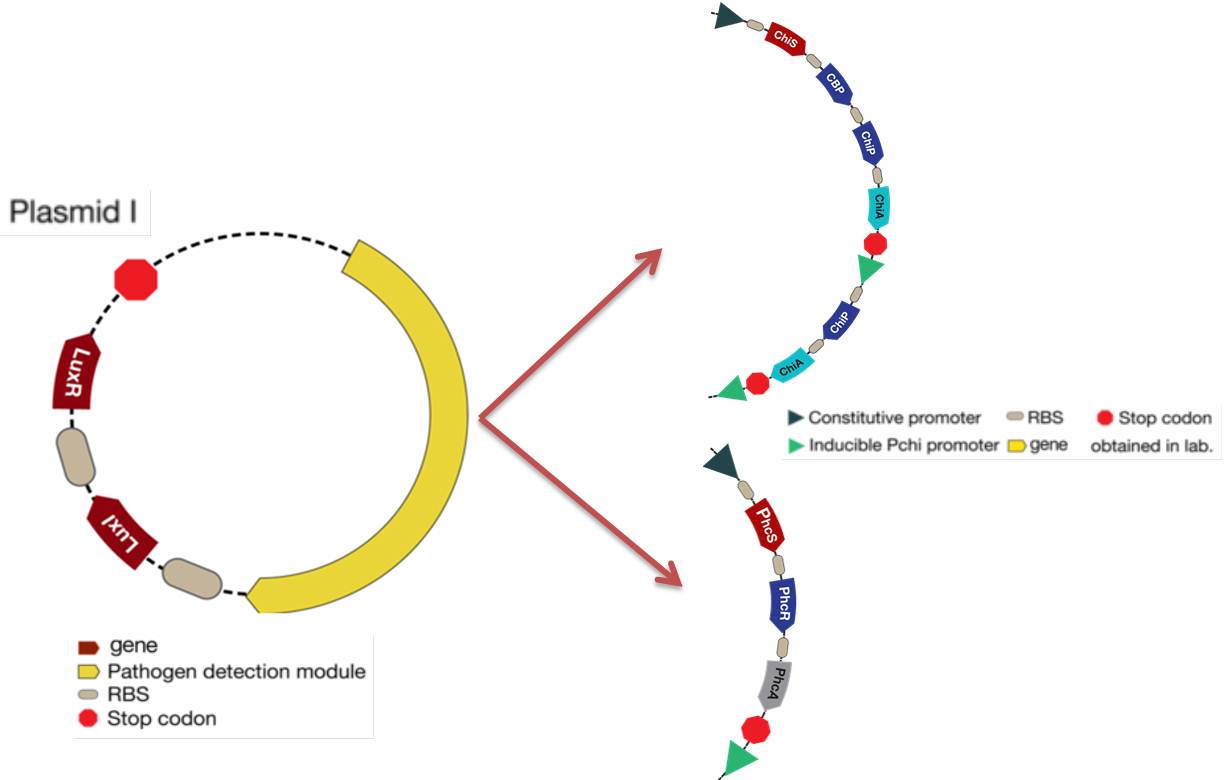
The mathematical model should help the experimental design to optimize the circuit and our case was not the exception. The picture below shows the original design of the circuit.
After doing the simulation for the differential equations we have to make little changes to the proposed system:
- As you can see there was an unknown promoter for LuxR. First we decided that it was a constitutive promoter but the response curves of the system were not consistent with the reality (LuxR had giant concentrations and the salicylic acid never went up). We wanted this protein to interact with LuxI and turn on the response, so we thought that it may need to be in a similar concentration of LuxI. Then we put it under the same promoter, hence the two proteins will be promoted at the same time.
- Our desired response is the increase of Salicylic Acid when a pest gets near the bacteria. With the original system the salicylic acid increased but not as much as we wanted, so to achieve this goal we tried putting the promoter activated by Lux next to the CI promoter to see if there was an increase. After running the simulation we discovered that this solution optimized the increase of salicylic acid in the response.
- Looking for the right set of parameters we came to the conclusion that the hill constant k (Concentration of the substrate when the the rate of production is half of the maximum production rate) for the promoter activated by Lux had to be 4 times greater than the hill constant for the CI promoter. Which has biological sense; the Lux promoter came from a quorum sensing system, so it needs high concentration of activator because it informs the promoter that there is high cell density. On the other hand the CI promoter box came from a bacteriophage and is used to attack the bacteria as quickly as possible, so it does need small quantities of protein to fully activate its system.
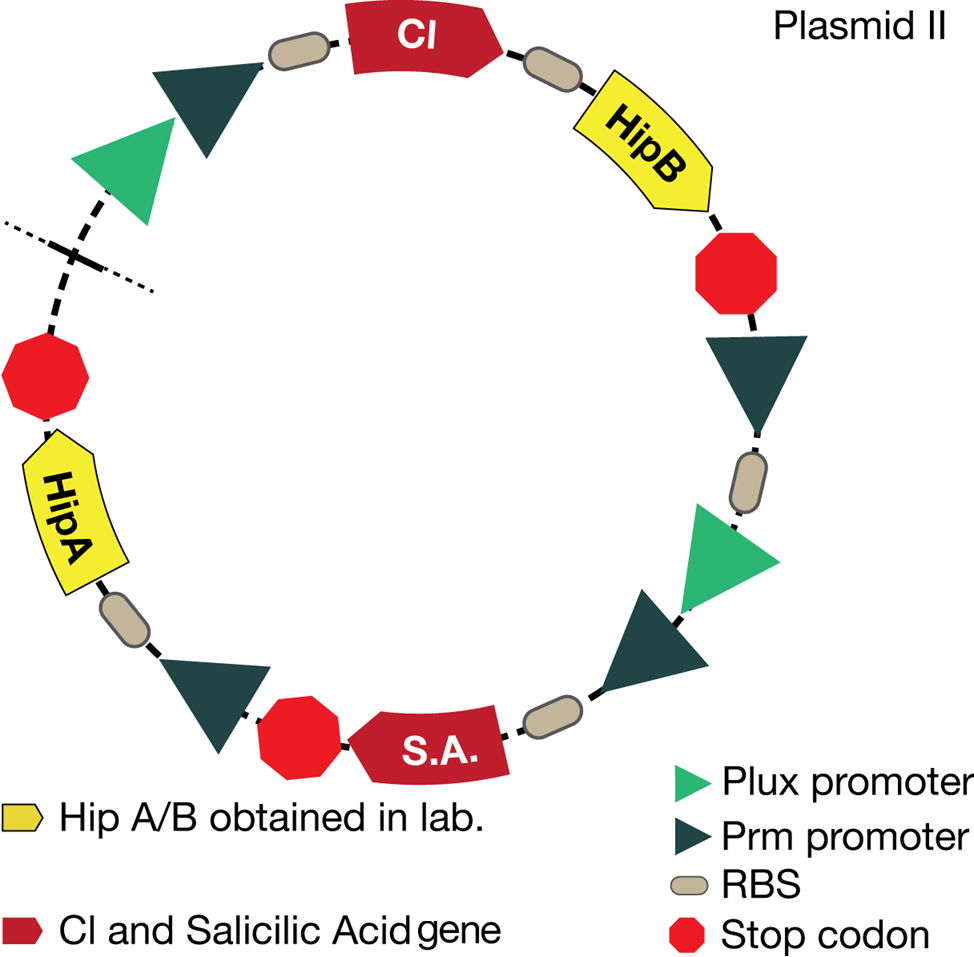
The new system is showed in the picture below:
Differential equations results
Although the screening of the parameters could not be completely done, we made a manual search for them and found a set that makes the system behave as expected. Here we present the mean response of all the substances in our biological system for one cell. The impulse of the pest was made during the times 10-20.
Ralstonia
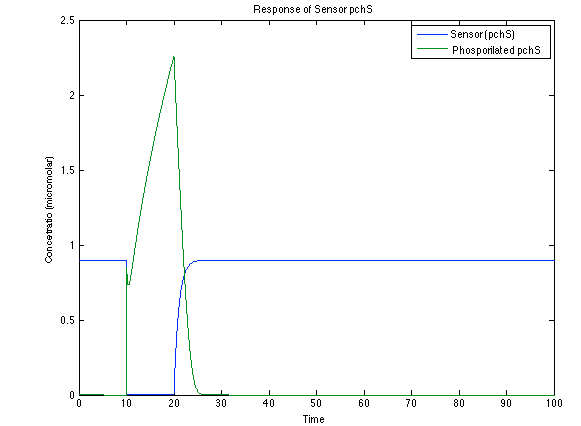
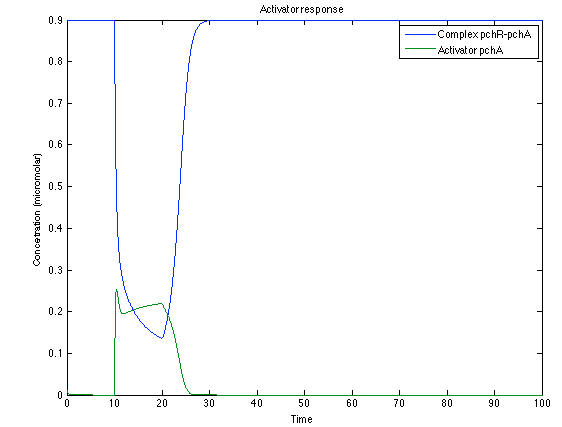
As you see below, when the system is under the presence of 3-OH-PAME the sensor is phosphorylated really fast and the complex phcR-phcA liberates the activator which has a peak and the goes a little down because is with the promoter and its not free. After the impulse is gone everything goes back to normality.
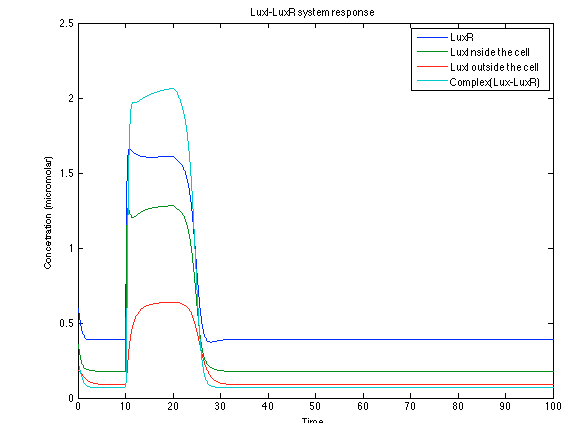
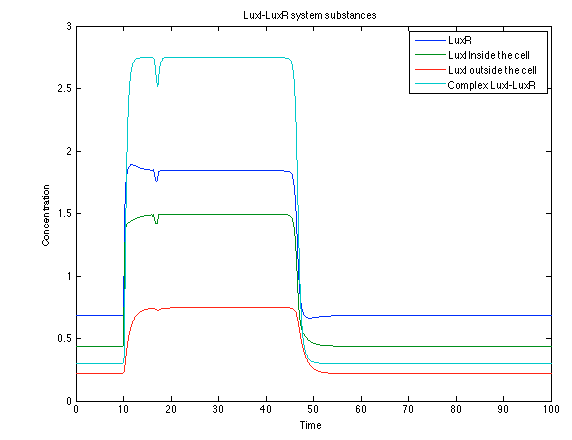
The LuxI- LuxR System shows and increase after it is activated by phcsA
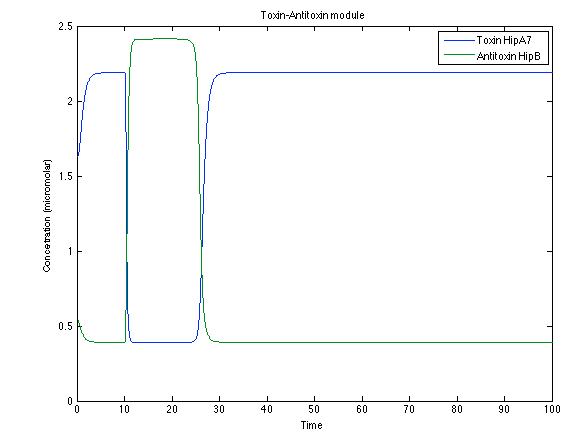
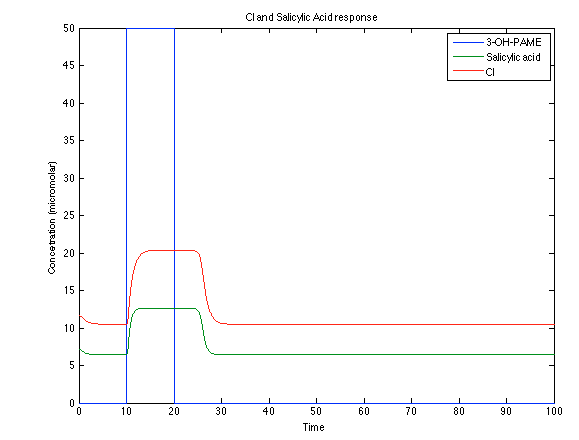
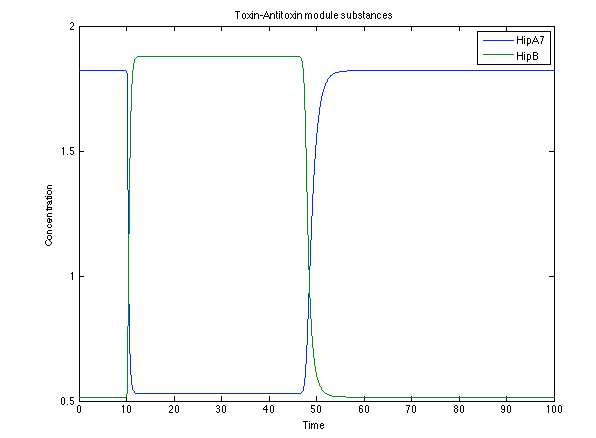
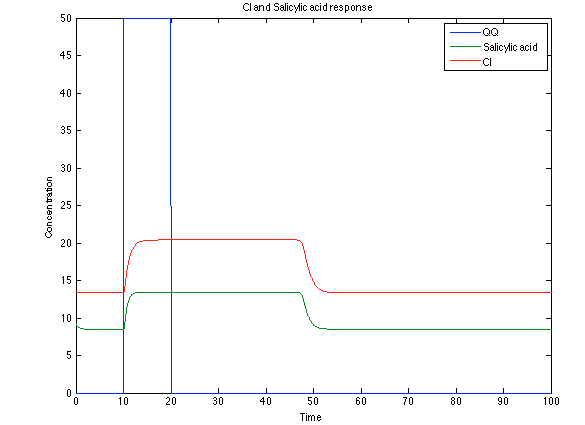
Now, looking at the species of interest, we can see how the antitoxin has greater concentration than the toxin when the 3-OH-PAME appears, this means that the cell is awake and can produce proteins. On the other hand, the Salicylic acid has an increase of almost two fold.
Rust:
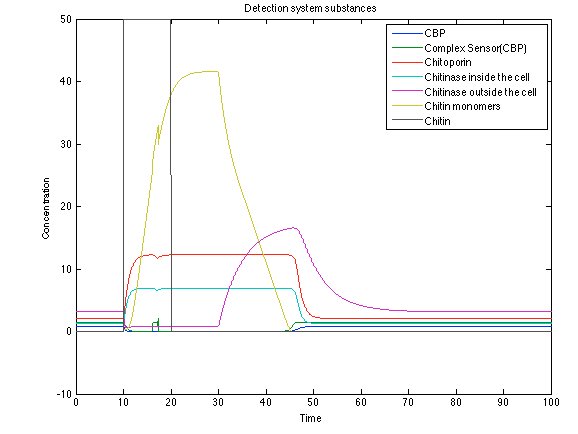
When the system is under the presence of chitin you can see how the positive feedback of the chitoporin and chitinase works and make their concentration increase. This has as a consequence the increase of monomers of chitin and the liberation of the sensor that is gonna activate the LuxI and LuxR promoter.
Like we see with the Ralstonia systema the Lux system's concentrations increase when their promoter is activated. The complex LuxI-LuxR has a peak and then goes down a little because it is busy activation of CI and Salicylic Acid.
The compounds od interest behave just like expected. Like in Ralstonia the cell is awake when the chitin is present and the Salicylic Acid has a two fold increase. It is important to see that this system takes more time to go back to the steady state than the Ralstonia's system.
Scripting
Differential equation solver
RALSTONIA
These scripts create the differential equations, find the steady state concetrations and then solve them by a 4th order Runge Kutta:
DIFFERANTIAL EQUATIONS DECLARATIONS
%THIS CODE CREATE ALL THE DIFFERENTIAL EQUATIONS FOR THE SYSTEM FOR %RASTONIA
function y=ecuaDifR(t,v)
%---------Parameters------%
global alfS %Basal concentration of the sensor phcS
global alfRA %Basal concnetration of the comple pchA-pchR
global alfR %Basal concentration of LuxR
global alfI %Basal concentration of CI
global alfCI %Basal concentration of CI
global alfHA %Basal concnetration of HipA7
global alfHB %Basal concnetration of HipB
global alfAS %Basal concnetration of Salycilic acid
global gammaS %Degradation of the sensor pchS
global gammaRA %Degradation of the complex pchR-pchA
global gammaR %Degradation of LuxR
global gammaI %Degradation of LuxI
global gammaCI %Degradation of CI
global gammaHA %Degradation of HipA7
global gammaHB %Degradation of HipB
global gammaAS %Dergradation of Salycilic acid
global mOHS %Kinetic constant for the detection of 3-OH-PAME by the sensor pchS (phosphorylation)
global mSFR %Kinetic constant for the phosphorylation of the complex pchR-pchA by the sensor
global mA %Kinetic constant for the activation of the promoter by the pchA
global mIR %Kinetic constant for the formation of the complex LuxILuxR
global mI %Constant that represent the union of the complex LuxILuxR with the promoter
global mHAHB %Kinetic constant for the inhibition of HipA7
global betaI %Max production of LuxI
global betaCI %Max production of CI
global betaHB %Max peoduction of HipB
global betaHA %Max production of HipA7
global betaAS %Max production of Salicylic acid
global kA %Constant k of the hill ecuation for the promoter promoted by pchA
global kIR %Constant k of the hill equiation for the promorer prmoted by the complex luxIluxR
global kCI %Constant k of the hill equation for the promoter promoted by CI
global hA %Hill constant for the promoters promoted by pchA
global hIR %Hill constant for the promoter promoted by the complex IR
global hCI %Hill constant fot the promoter CI
global eI %Export factor of LuxI
global jI %Import factor of LuxI
global deltaI %Difusion of LuxI outside the cell
global eAS %Export of Salicylic acid
global numcel %number of cells
if (t<(10) || ((t)>20))
OH=0;
else
OH=15;
end
%------ Variables%------
S=v(1); %Cocentration of the sensor pchS the cell
SF=v(2); %Concentration of phosphorylated sensor the cell
RA=v(3); %Concentration of the comple pchR-pchA
A=v(4); %Concentratio of the promoter avtivator pchA
Ii=v(5); %Concentration of LuxI inside the cell
Io=v(6); %Concentration of LuI outsied the cell
IR=v(7); %Concentration of the complex LuxI-LuxR
R=v(8);%Concentration of the protein CI
CI=v(9);%Concentration of HipA7
HB=v(10);%Concnetratio of HipB
HA=v(11);%Concentration of salicylic acid
AS=v(12); %Concentratio of quitin monomers
%---Equations---%
dS=alfS- gammaS*S - mOHS*OH*S; %Change of the sensor pchS
dSF = mOHS *OH*S - mSFR *SF*RA ; %Change of phosphorylated sensor
dRA=alfRA - gammaRA*RA - mSFR*SF*RA;%Change of the comple pchR-pchA
dA= mSFR*SF*RA-mA*A; %Change of the activator pchA inside the cell
dIi= alfI+ (betaI*(A^hA))/(kA^hA+(A^hA)) -gammaI*Ii +jI*Io- eI*Ii- mIR*Ii*R; %Change of LuxI inside the cell
dIo= numcel*(eI*Ii-jI*Io)-deltaI*Io; %Change of LuxI outside the cell
dIR= mIR*Ii*R - mI*IR; %Change of the complex LuxI luxR
dR= alfR-gammaR*R -mIR*Ii*R +(betaI*(A^hA))/(kA^hA+(A^hA)); %Change of LuxR
dCI= alfCI -gammaCI*CI+ (betaCI*(CI^hCI))/(kCI^hCI+(CI^hCI)) +(betaCI*(IR^hIR))/(kIR^hIR+(IR^hIR));%Change of CI
dHB=alfHB-gammaHB*HB+(betaHB*(CI^hCI))/(kCI^hCI+(CI^hCI))+(betaHB*(IR^hIR))/(kIR^hIR+(IR^hIR))-mHAHB*HA^2*HB^2; %Chanche of HipB
dHA=alfHA-gammaHA*HA+ (betaHA*(CI^hCI))/(kCI^hCI+(CI^hCI))-mHAHB*HA^2*HB^2; %Change of HipA7
dAS=alfAS-gammaAS*AS +(betaAS*(CI^hCI))/(kCI^hCI+(CI^hCI))-eAS*AS+(betaAS*(IR^hIR))/(kIR^hIR+(IR^hIR)); %Change of Salicylic acid
y1(1)=dS;
y1(2)=dSF;
y1(3)=dRA;
y1(4)=dA;
y1(5)=dIi;
y1(6)=dIo;
y1(7)=dIR;
y1(8)=dR;
y1(9)=dCI;
y1(10)=dHB;
y1(11)=dHA;
y1(12)=dAS;
y=y1';
end
RUNGE KUTTA
%FILE THAT SOLVES THE DIFFERENTIAL EQUATION AND GRAPHS THEM alfS=0.9; %Basal concentration of the sensor pchS alfRA=0.9; %Basal concnetration of the complez pchA-pchR alfR=0.6; %Basal concentration of LuxR alfI=0.4; %Basal concentration of LuxI alfCI=0.5; %Basal concentration of CI alfHA=1; %Basal concnetration of HipA7 alfHB=0.4; %Basal concnetration of HipB alfAS=0.4; %Basal concnetration of Salycilic acid gammaS=1; %Degradation of Chitinase inside the cell gammaRA=1; %Degradation of chitoporin gammaR=1; %Degradation of LuxR gammaI=1; %Degradation of LuxI gammaCI=1; %Degradation of CI gammaHA=1; %Degradation of HipA7 gammaHB=4; %Degradation of HipB gammaAS=1; %Dergradation of Salycilic acid mOHS=4; %Kinetic constant for the formation of the phoshorilation of the sensor mSFR=2.6; %Kinetic constant of the reaction of the phosphorilarion of the comple R mA=3.5; %Kinetic constant for the activation by A mIR=3; %Kinetic constant for the formation of the complex LuxILuxR mI=3; %Constant that represent the union of the complex LuxILuxR with the promoter mHAHB=12; %Kinetic constant for the inhibition of HipA7 betaI=10; %Max production of LuxI betaCI=9.96; %Max production of CI betaHB=9.95; %Max production of HipB betaHA=10; %Max production of HipA7 betaAS=11.2; %Max production of Salicylic acid kA=0.1; %Constant k of the hill ecuation for the promoter promoted by S kIR=0.39; %Constant k of the hill equiation for the promorer prmoted by the complex luxIluxR kCI=0.055; %Cosntant k of the hill equation for the promoter promoted by CI hA=1.2; %Hill constant for the promoters promoted by S hIR=3.4; %Hill constant for the promoter promoted by the complex IR hCI=2.3; %Hill constant fot the promoter CI eI=0.5; %Export factor of LuxI jI=0.8; %Import factor of LuxI deltaI=0.2;%Difusion of LuxI outside the cell eAS=0.8; numcel=1; %number of cells %----%
h=100; %Tiempo maximo m=0.01; %Longitud de paso [s] t=0:m:h; %Vector tiempo xi=[1,1,1,1,1,1,1,1,1,1,1,1]; y=fsolve(@CondInR,xi);
conInd=y;
l=(0:m:h)'; %Vector de tiempo
x=zeros(length(l),length(conInd)); %Matriz de variables, en las columnas varia
%la variable y en las filas varia el tiempo
OH=zeros(1,length(l));
x(1,:)=conInd;
for k=1:length(l)-1
xk=x(k,:); %Captura de la ultima posicion de la matirz, es decir, los
%valores actuales de las variables
k1=ecuaDifR(l(k),xk); %Primera pendiente del metodo de RK4
k2=ecuaDifR(l(k)+m/2,xk+(m/2*k1)'); %Segunda pendiente del metodo de RK4
k3=ecuaDifR(l(k)+m/2,xk+(m/2*k2)'); %Tercera pendiente del metodo de RK4
k4=ecuaDifR(l(k)+m,xk+(m*k3)'); %Cuarta pendiente del metodo de RK4
xk1=xk+m/6*(k1+2*k2+2*k3+k4)'; %Calculo de nuevos valores para las
%variables
%xk1=xk+m*ecuaDif(l(k),xk)'; %Method of Newton
xk2=zeros(1,length(xk1));
for p=1:length(xk1)
if(xk1(p)<0.00000001)
xk2(p)=0;
else
xk2(p)=xk1(p);
end
end
x(k+1,:)=xk2; %Actualizacion del nuevo vector de variables en la matriz
end
for j=1:length(l)
if (l(j)<(10) || l(j)>(20))
OH(j)=0;
else
OH(j)=15;
end
end
S=x(:,1); SF=x(:,2); RA=x(:,3); A=x(:,4); Ii=x(:,5); Io=x(:,6); IR=x(:,7); R=x(:,8); CI=x(:,9); HB=x(:,10); HA=x(:,11); AS=x(:,12);
figure(1)
plot(l,S,l,SF)
legend('Sensor (pchS)',' Phosporilated pchS')
xlabel('Time')
ylabel('Concetratio (micromolar)')
title('Response of Sensor pchS')
figure(5)
plot(l,RA,l,A)
legend('Complex pchR-pchA','Activator pchA')
xlabel('Time')
ylabel('Concetration (micromolar)')
title('Activator response')
figure(2)
plot (l,R,l,Ii,l,Io,l,IR)
legend('LuxR','LuxI nside the cell','LuxI outside the cell','Complex(Lux-LuxR)')
xlabel('Time')
ylabel('Concetration (micromolar)')
title('LuxI-LuxR system response')
figure(3)
plot (l,HA,l,HB)
legend('Toxin HipA7','Antitoxin HipB')
xlabel('Time')
ylabel('Concetration (micromolar)')
title('Toxin-Antitoxin module')
figure(4)
plot (l,OH,l,AS,l,CI)
legend('3-OH-PAME','Salicylic acid','CI')
xlabel('Time')
ylabel('Concetration (micromolar)')
title('CI and Salicylic Acid response')
 "
"