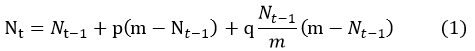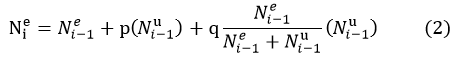Team:Tianjin/Modeling/HGTBass
From 2012.igem.org
(→Rudimentary Model) |
(→The Effects of Parameters on the Shape of the Curve) |
||
| Line 174: | Line 174: | ||
===The Effects of Parameters on the Shape of the Curve=== | ===The Effects of Parameters on the Shape of the Curve=== | ||
| + | In order to study how the parameters impact the shape of the curve, we changed the two important parameters p and q in the formula, and also compared the shapes of the curves under different conditions. | ||
| + | |||
| + | First of all, we studied how the increasing of p impacts the shape of the curve. The diagram of curves at the three different p is shown in '''Fig. 2'''. | ||
| + | [[file:TJU2012-Mode-HGT-fig-2.png|thumb|500px|center|'''Figure 2.''' ]] | ||
| + | |||
| + | It is not difficult to conclude that the number of E bacteria will increase much faster when the parameter p increased. So the mutagenesis will increase the speed of the percentage of E. bacteria. | ||
| + | |||
| + | After that, we studied how the increasing of q impacts the shape of the curve. The diagram of curves at the three different q is shown in '''Fig. 3'''. | ||
| + | [[file:TJU2012-Mode-HGT-fig-3.png|thumb|500px|center|'''Figure 3.''' ]] | ||
| + | |||
| + | It is easy to conclude that the number of E bacteria will increase much faster when the parameter q increased. So the other method to increase the probability of HGT will increase the increasing speed of the percentage of E. bacteria. | ||
=Final Model= | =Final Model= | ||
Revision as of 19:33, 24 September 2012

Contents |
Background
Genetic pollution is the term of genetics in which the genetic information is transferred in to the organisms where it is not needed or where this information never existed before. This flow of genetic information is usually undesired and cannot be controlled. The flow of genetic information usually takes place between the genetically modified organisms into the organisms which are not genetically modified.
Unlike other forms of pollution, genetic contamination has the potential to be a problem that multiplies as plants and microorganisms grow and reproduce. Therefore, environmental damage caused by genetically modified organisms (GMOs) cannot be confined to the original habitat. This briefing considers what is known about these risks and the evidence that is emerging from experimental and commercial growing of GE crops.
Horizontal gene transfer (HGT), also lateral gene transfer (LGT) or transposition refers to the transfer of genetic material between organisms other than vertical gene transfer.
HGT is the primary reason for bacterial antibiotic resistance. Genes that are responsible for antibiotic resistance in one species of bacteria can be transferred to another species of bacteria, subsequently arming the antibiotic resistant genes' recipient against antibiotics.
Due to the increasing amount of evidence suggesting the importance of these phenomena for evolution molecular biologists such as Peter Gogarten have described HGT as "A New Paradigm for Biology".
Our Problem
There are two ways for wild type bacteria to have some exogenous gene. To make it more convenient to distinguish between the two type of bacteria, we call the bacteria containing exogenous gene the E bacteria. Similarly, the wild type bacteria are called the W ones. We want to study how the exogenous gene horizontally transferred from to other bacteria and how the number of W bacteria and E bacteria changed with time.
Our Experiment Design
We studied the how the number of E. bacteria increased with mutation and HGT. This is an important reason for the genetic pollution.
In our experiment, we have cultivated some W bacteria in the substrate whose initial number is N0w. At the same time, we induce E bacteria, the same bacteria as the W ones but contains the exogenous gene on their plasmid. The initial number of the evil bacteria is N0e.
We will test the number of E and W bacteria every other ∆t, while ∆t is the generation time. We assume the generation time of the W and E bacteria are identical because they belong to the same species.
Model Inspiration: Bass Diffusion Model
The Bass diffusion model was developed by Frank Bass and describes the process of how new products get adopted as an interaction between users and potential users. Mathematically, the basic Bass diffusion is a Riccati equation with constant coefficients. This model has been widely influential in marketing and management science. What is more, the mathematic concept has also inspired me. Before our description of our model, we had better get to know the details of the Bass model. The formula of our model is listed as equation (1).
In equation (1), the Nt represents the number of consumers who have purchased the product when time is t, represents the total number of consumers and potential consumers, p is the coefficient of innovation which stands for the degree of how the consumers tend to try new things. While q is the coefficient of imitation which stands for the degree of how the consumers tend to be imitate other people who are trying the products.
This is the Bass model that inspired us about how the gene transfer horizontally.
Rudimentary Model
The rudimentary version model is extraordinarily similar to the Bass model in equation (2), but the meaning of all the parameters and coefficient.
In the equation, Niestands for the number of E bacteria at the time=i×∆t. Niw stands for that of the wild type bacteria. However, in this model, the coefficient p and q has very different meaning. The coefficient p stands for the probability of the exogenous gene resulting from the mutation; and the coefficient q stands for the probability of the exogenous gene resulting from the HGT. The interval is the generation time of the bacteria.
In this rudimentary model, we assume the total number of E and W bacteria is constant. The number of E bacteria increased is only due to the HGT and the gene mutations. To be more specific, the number of increased is proportional to that of the percent of E bacteria and the number of W ones. The diagram is shown in Fig. 1.
The Effects of Parameters on the Shape of the Curve
In order to study how the parameters impact the shape of the curve, we changed the two important parameters p and q in the formula, and also compared the shapes of the curves under different conditions.
First of all, we studied how the increasing of p impacts the shape of the curve. The diagram of curves at the three different p is shown in Fig. 2.
It is not difficult to conclude that the number of E bacteria will increase much faster when the parameter p increased. So the mutagenesis will increase the speed of the percentage of E. bacteria.
After that, we studied how the increasing of q impacts the shape of the curve. The diagram of curves at the three different q is shown in Fig. 3.
It is easy to conclude that the number of E bacteria will increase much faster when the parameter q increased. So the other method to increase the probability of HGT will increase the increasing speed of the percentage of E. bacteria.
 "
"