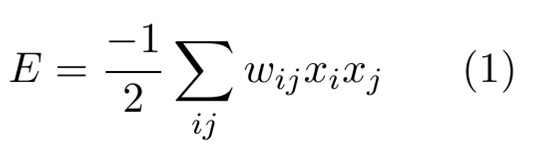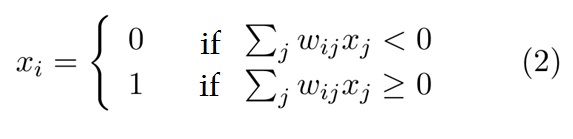"
Team:USP-UNESP-Brazil/Associative Memory/Background
From 2012.igem.org
(→Hopfield Associative Memory Networks) |
(→Hopfield Associative Memory Networks) |
||
| Line 6: | Line 6: | ||
The architecture, or geometry of the system, is composed in a way that all neurons are connected .In math terms, a Hopfield Network can be represented as an “Energy” (E) function: | The architecture, or geometry of the system, is composed in a way that all neurons are connected .In math terms, a Hopfield Network can be represented as an “Energy” (E) function: | ||
| - | [[File:equation1.jpg|center| | + | [[File:equation1.jpg|center|300px|caption|]] |
Where “w” values are chosen such that the stored settings are the minima of the function “E”. The variable “x” is the state of the neuron “i”. | Where “w” values are chosen such that the stored settings are the minima of the function “E”. The variable “x” is the state of the neuron “i”. | ||
Revision as of 04:31, 22 September 2012
IntroductionProject OverviewPlasmid Plug&PlayAssociative MemoryNetwork
ExtrasHopfield Associative Memory Networks
The main model of the project is the associative memory network made by J.J. Hopfield in the 80’s. On this model, the system tends to converge to a pre-determined equilibrium, restoring the same pattern when exposed to variations of this same pattern.
The architecture, or geometry of the system, is composed in a way that all neurons are connected .In math terms, a Hopfield Network can be represented as an “Energy” (E) function:
Where “w” values are chosen such that the stored settings are the minima of the function “E”. The variable “x” is the state of the neuron “i”.
The state of a given neuron “I”(active or silent) can be mathematically represented as follows: Given that “xi“ is the state of neuron, 1 if is activated or 0 if silent, and a neuron turns active if the sum of all received stimulus (exciting or inhibiting) is more than 0. Mathematically we can represent the state of the neuron xi as:
