Team:SEU A/Modeling
From 2012.igem.org
(Difference between revisions)
| (2 intermediate revisions not shown) | |||
| Line 94: | Line 94: | ||
<li class="toclevel-2 tocsection-4"><a href="#.B4"><span class="tocnumber"> 2.4</span> <span class="toctext">Shortcomings and improvements</span></a></li> | <li class="toclevel-2 tocsection-4"><a href="#.B4"><span class="tocnumber"> 2.4</span> <span class="toctext">Shortcomings and improvements</span></a></li> | ||
<li class="toclevel-2 tocsection-5"><a href="#.B5"><span class="tocnumber"> 2.5</span> <span class="toctext">Reference</span></a></li> | <li class="toclevel-2 tocsection-5"><a href="#.B5"><span class="tocnumber"> 2.5</span> <span class="toctext">Reference</span></a></li> | ||
| + | <li class="toclevel-2 tocsection-5"><a href="#.B6"><span class="tocnumber"> 2.6</span> <span class="toctext">Download</span></a></li> | ||
</ul> | </ul> | ||
</li> | </li> | ||
| Line 264: | Line 265: | ||
The simulation results are shown as below:</br> | The simulation results are shown as below:</br> | ||
| + | |||
| + | </b><center><img src='https://static.igem.org/mediawiki/2012/thumb/4/40/Seua_m1.jpg/800px-Seua_m1.jpg'></img></center></b> | ||
Wherein C2 = 4, C1 = 1, γ1 = 0, γ2 = 6, Ψ2 (R) = 1.0, Ψ2 (D) = Ψ2 (T) = 0.9, τ = 0.005, p = 1.0,</br> | Wherein C2 = 4, C1 = 1, γ1 = 0, γ2 = 6, Ψ2 (R) = 1.0, Ψ2 (D) = Ψ2 (T) = 0.9, τ = 0.005, p = 1.0,</br> | ||
| Line 272: | Line 275: | ||
As is shown in the picture, the best ratio of D and R is 3:2. The simulation is terminated as nutrients running out. The final state of the two layers of bacteria are shown below:</br></br> | As is shown in the picture, the best ratio of D and R is 3:2. The simulation is terminated as nutrients running out. The final state of the two layers of bacteria are shown below:</br></br> | ||
| + | |||
| + | </b><center><img src='https://static.igem.org/mediawiki/2012/thumb/d/d0/Seua_m2.jpg/800px-Seua_m2.jpg'></img></center></b> | ||
| + | </b><center><img src='https://static.igem.org/mediawiki/2012/thumb/1/1f/Seua_m3.jpg/800px-Seua_m3.jpg'></img></center></b> | ||
<span class="mw-headline" id=".B4"><font size=5><strong>2.4 Shortcomings and improvements</font></strong></span></br></br> | <span class="mw-headline" id=".B4"><font size=5><strong>2.4 Shortcomings and improvements</font></strong></span></br></br> | ||
| Line 287: | Line 293: | ||
[4]IGEM_Berkeley Team of IGEM-2005. Part: BBa_J01003: Experience[EB/OL]. <a href='http://partsregistry.org/Part:BBa_J01003:Experience'>http://partsregistry.org/Part:BBa_J01003:Experience</a>, 2005-10-18</br></br> | [4]IGEM_Berkeley Team of IGEM-2005. Part: BBa_J01003: Experience[EB/OL]. <a href='http://partsregistry.org/Part:BBa_J01003:Experience'>http://partsregistry.org/Part:BBa_J01003:Experience</a>, 2005-10-18</br></br> | ||
| + | |||
| + | <span class="mw-headline" id=".B6"><font size=5><strong>2.6 DownloadReferences</font></strong></span></br></br> | ||
| + | |||
| + | You may download pdf. version of this article here:</br></html>[[Media:The SDTC Model (iGEM 2012 SEU A Model).pdf | The SDTC Model (iGEM 2012 SEU A Model).pdf]]<html> | ||
| + | |||
</div> | </div> | ||
Latest revision as of 04:02, 27 September 2012

modeling
The ebb and flow of E. coli in computer..
Index |
1 Analysis of E.coli and Bdellovibrio’s growth in the number of speed by a group of photographs
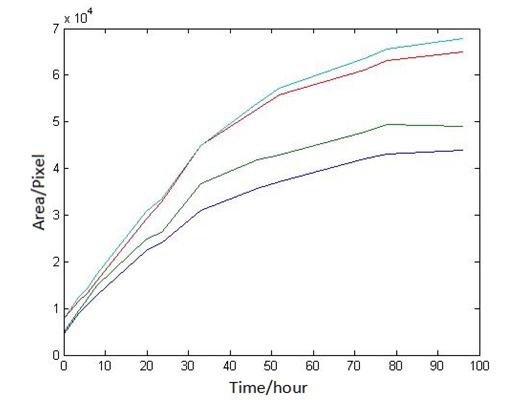
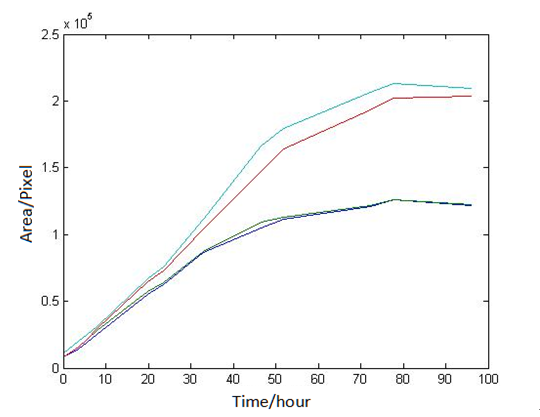
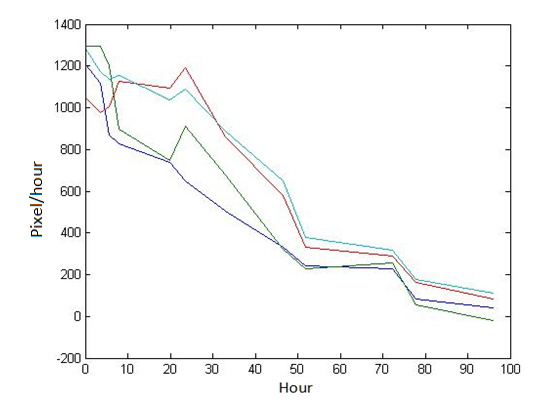
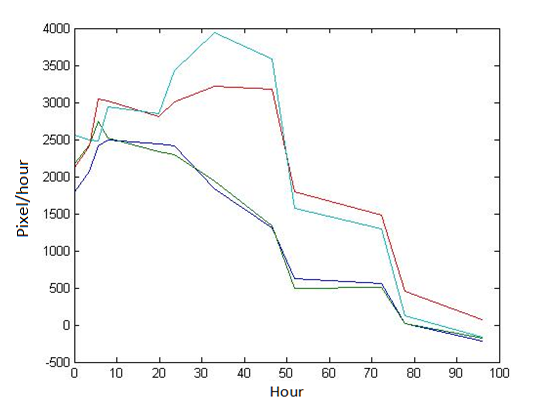
Abstract: Based on the observations at intervals of several days, and the photos of the plaque in the process of E. coli and Bdellovibrio group’s growth in the same dish taken at a high resolution for experimental, we use of the image processing functions of Matlab to simplify the statistics and calculate the relative quantities of the two bacteria at the observation time in the dish. The results also verify whether the experimental results conform to the classical S-shaped curve, and estimate the bacterial growth rate in every moment, in order to analyze the bacterial growth’s features under the conditions of the experiments. Key words: Bacterial growth High resolution photos Image processing S-shaped curve fitting. 1.1 The classical model of the flora growth Under normal circumstances, a growth curve can be obtained with the time as abscissa and the logarithmic of the number of viable cells as ordinate. The curve shows the four periods of the bacterial growth and reproduction: the lag period, the logarithmic period, the stable period, the decline period. The lag period is the transient process the bacteria adapt to the new environment after being inoculated to the medium. In this period, the curve is flat and stable because of slow bacterial multiplication. The number of viable bacteria will soar when it reaches the logarithmic period. The bacteria will grow at stable geometric series, and can last sustainably hours and days (depending on the conditions and bacterial generation). Moreover, bacteria’s form, dyeing and biological activity in this period are all very typical which is sensitive to environmental factors, so it’s the best period to research the bacterial traits. When it reaches the stable period, however, the total number of flora is in the flat stages due to the relative relationship of nutrition and the number of bacteria, but bacterial viability changes greatly. Finally, bacterial growth will get slower in the decline period, and the number of the dead bacteria will apparently increase. In addition, the number of viable cells and the incubation time are in inversely proportional relationship. Mastering the bacterial growth’s law, we can study the method of controlling the growth of pathogenic bacteria, discovering and developing bacteria useful to human. 1.2 Assumptions and simplifications 1. Imagine that plaque is dense, that is to say, it’s always a simply connected area in surface of the two-dimensional dish. 2. Imagine that the plane occupied by the plaque in the culture dish is proportional to the number of bacteria in it. 3. Under the experimental conditions, imagine that E. coli is the only food of Bdellovibrio, and nutrients of E. coli are provided by the medium sufficiently. 4. The occasional small amount of bacteria in the edge of dish is ignored, and dripping or splashing a small amount of bacteria into the location of the error place in the initial state is considered to have no impact on the normal experimental bacteria. 5. After appropriate image processing, the light and its changes’ effects to the photos are ignored. 6. As to the fuzzy edge of the plaque, the area is considered to be the largest and smooth edges simply connected region. 1.3 Assumptions 3.1 Photos’ preprocessing 1. Select photos artificially. Remove the ones whose light effects apparently different from most of the photos, as well as the ones which appear the situation that two plaque overlap and stick together and the overlapping area is large in the later observations, so as not to increase the difficulties of unified image processing. 2. Rename all the photos by unified format. The format is ‘experimental group + days + hours + minutes xxx’, (such as ‘3111111’ meaning the third group at 11:11 on the 11th), which is beneficial to the unified automatic processing. 3. The few overlapping points of two plaques are considered to have no effects on these two, so use Photoshop to change the connections as the background color, in order to processing uniformly. 3.2 Calculation of the plaques’ area 1. After reading the photos, select the appropriate threshold to transform the photos into a binary image, according to the light conditions. 2. Identify all the connected regions, and remove the smaller ones (maybe caused by useless bacteria or lens’ dust). 3. Because of the light and its reflection in every photo, the edges of culture dishes are always lit, which require removing the large connective regions in the edges. 4. Calculate the area of the other connective regions, which is all the plaque area. 5. Use the area above as the relative number of bacteria, and pixel as the unit. Similarly, the number of bacteria growth rate is in unit of pixel/ unit time. And it is the same way if ‘the number of bacteria’, ‘the relative quantities of the bacteria’ and ‘the rate of bacteria growth’ in the paper is not particularly described. 1.4 Results and analysis 4.1 Figure of the changes in the number of E. coli and Bdellovibrio(4-1)
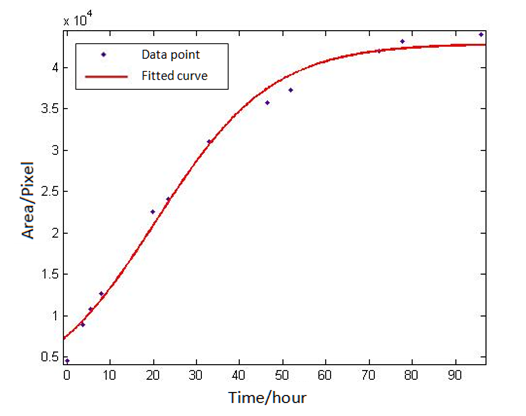
Where A,B,C are unknown parameters. Use ‘cftool’ in Matlab to fit the eight groups of data of the eight plaques, with the default method of least squares. After selecting the appropriate initial value for the three parameters, the results can be obtained quickly. By the fitting of eight groups of data, we found all the right parameters A,B,C to make data points distributing on both sides of the fitted curve and variance is small. If so, it is considered that the eight groups of data conform to the S-shaped curve, and that the image processing above is reliable The fitting results of a particular group are as follows:2 A Spatial Model of Plasmid Conjugation Transfer on an Agar Surface
2.1 Summary There are two main kinds of scheme to do the bacterial plasmid conjugation experiment: in well-mixed solution, or on solid culture such as agar surface. To spread the ‘death gene’ better in our ‘toxic apple’ project, we want to do some research on how to improve the conjugation efficiency under certain conditions. IGEM_Berkeley Team of IGEM 2005 have done some experiment on conjugation in solution and gave the best ratio between initial D(donor cells, similarly hereafter) and R(recipient cells) as 1:2. However, aimed to improve the conjugation efficiency, we consider the experiment and analysis of conjugation in solution are with these disadvantages: 1. The process of the experiment is difficult to be seen by an electron microscope. 2. The result is random in a certain degree due to the large space that cells could freely move in and the complex dynamics system of cells in the solution. 3. Mixing the solution is a necessary step to help D and R contact while it may also interrupt the conjugation itself. Taking the reasons above into consideration, we decided to model for the scheme on solid culture. Due to the limited time in our experiment, we use some parameters from others’ experiment and modeling and we also use the SDTC model to get the best ratio between initial D and R with the total number of initial plasmid donor cells and recipient cells constant by simulation. In our SDTC model, we employ a lattice of 500×500 to describe each cell and each sites in simulation lattice area separately so we can trace their state separately at any time. We use a ‘Cycle Time Trace’ system to record each cell’s doubling and conjugation state and ensure they update asynchronously so that the time in our system could be considered as continuous compared with the scale of cell doubling time or conjugation cycle time though any kind of simulation of time has to use a small period of time as simulation step length and we make no exception. 2.2 Model 2.1 Space system In the SDTC Model, we set up a 500×500 lattice which contain 250000 sites. Bacteria and nutriment can be at any site on the lattice. The bacteria cell is considered 1 um2 that the total area of our view window is 0.25mm2. Furthermore, the lattice can be extended to more than 2 dimension. The thickness of lattice has three possible value: 0, 1, 2, that is to say, each site can hold mostly two kind of bacteria at the same time. In addition, there is no such ‘up and down’difference inside one site in this 2.5D model. The thickness of nutriment is 0. The reasons why we set this model like this are as follows: 1. The model abstracts the thickness of bacteria into three levels, making the modeling and simulation able to be built and operated in several lattices, which greatly reduces the difficulty of modeling and the time of simulation. 2. Some three-dimensional properties are added to the SDTC model. For example, the filial generation comes out randomly around the parental generation. If the two layers of the neighborhood were taken over, the division will however be controlled. In a word, the SDTC model is a 2.5D model. 3. The model also largely simplifies the judgment of donor cell and receptor cell in conjugation (the conjugation occurs only when the donor cell and receptor cell are at the same site). We introduce the conception of ‘neighborhood’ in our plane domain and divide it into ‘bacteria neighborhood’ and ‘nutriment neighborhood’. As to any point, the bacteria of the bacterial neighborhood mean all the bacteria in the center of the 3 × 3 square area; similarly, the nutrition of the nutrient neighborhood refers to the nutrient in the center of the 7 × 7 square area. The detailed reasons of setting like this were discussed in Reference [2]. It is considered that bacteria can reproduce and transfer only within a certain distance due to the use of agar medium, but bacteria and nutrients cannot move. This is the fundamental difference between this model and the model in solution. 2.2 Bacterial and nutrient system E. coli can be divided into three categories: D-donor, R-receptor, T-conjugative transfer receptor. Considering the bacterial horizontal conjugative transformation and reproduction, their speeds are related to the quantity of nutrients in the neighborhood, which is conformed to the beta function (a sigmoidal function). Specifically, there are two thresholds - the lower one C1 and the upper one C2. When the quantity of nutrients in the neighborhood C


Biomedical Engineer School, SEU | iGEM 2012
Copyright © Southeast University iGEM 2012 Team A, All rights reserved.
 "
"