Team:USP-UNESP-Brazil/Associative Memory/Background
From 2012.igem.org
(→Hopfield Associative Memory Networks) |
|||
| (59 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{:Team:USP-UNESP-Brazil/Templates/Header}} | {{:Team:USP-UNESP-Brazil/Templates/Header}} | ||
| + | |||
| + | =Background= | ||
| + | |||
===Hopfield Associative Memory Networks=== | ===Hopfield Associative Memory Networks=== | ||
| - | The | + | The idea of this project is based on the associative memory network introduced by J.J. Hopfield in the 80’s [http://en.wikipedia.org/wiki/Hopfield_network]. The structure of a Hopfield network is simple, all neurons are interconnected, and that brings about some interesting memory properties and provides a model for understanding human memory. |
| + | |||
| + | We have chosen to built a Hopfield network because of its simplicity and robustness. The same methodology can be used to the construction of networks with different architectures, such as the called “perceptrons” [http://en.wikipedia.org/wiki/Perceptron]. In contrast to a Hopfield network, a perceptron is commonly used as a classifier. | ||
| + | |||
| + | ===Biological Mechanism=== | ||
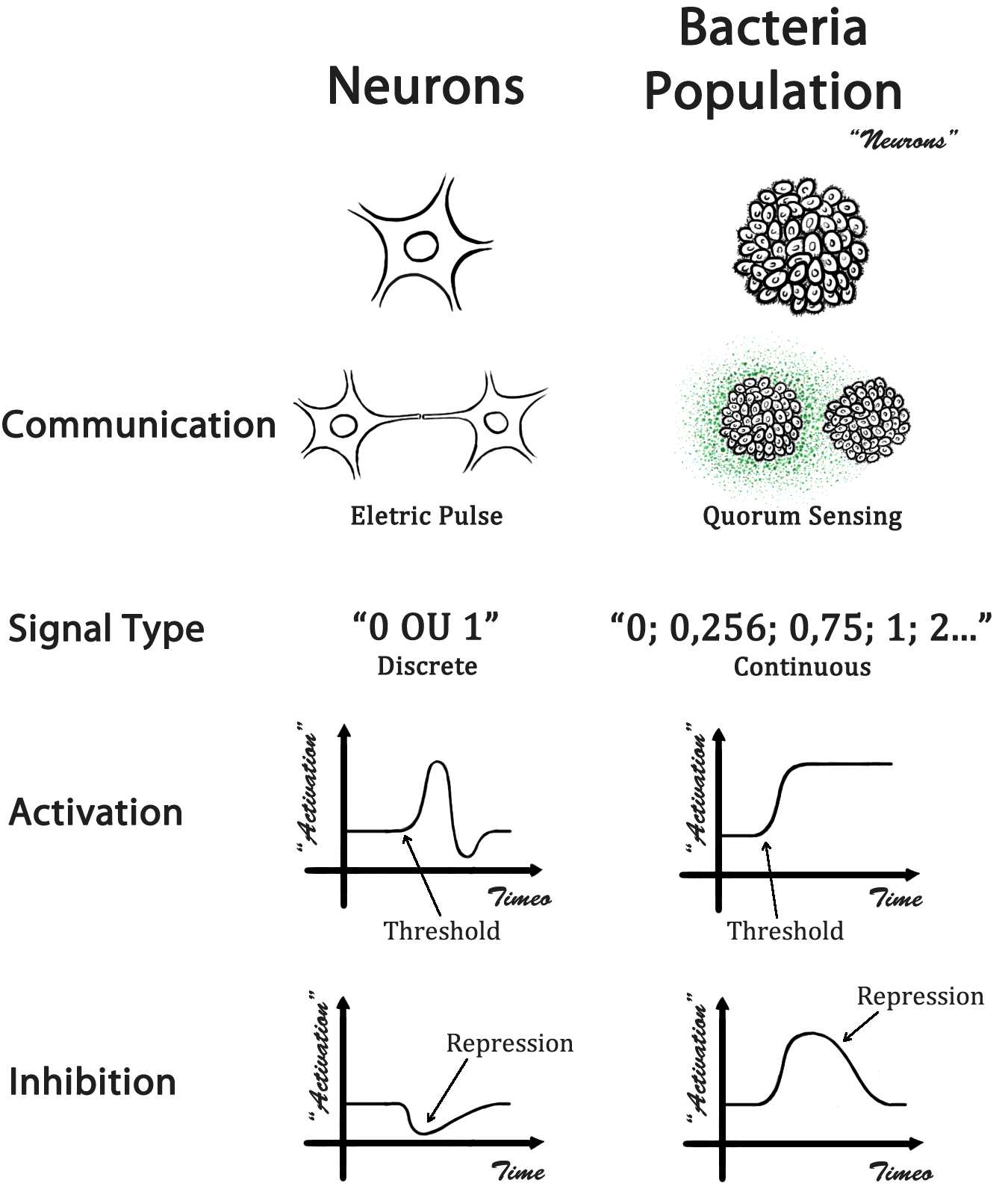
| + | In a biological neural network, cells occupy a specific location and the information is passed through direct physical contact - the neuron axonal projections. In our case, a population of bacteria represents a single neuron and the information is transmitted by a quorum sensing molecule (QSM). Because of that, each "neuron" has its own QSM and the number of neurons is limitated by the number of different QSM. A comparison between a biological neural network and our design is presented in Fig 1. | ||
| + | |||
| + | {{:Team:USP-UNESP-Brazil/Templates/RImage | image=Figura0020.jpg | caption=Fig 1. Comparison between a biological neural network and "bacterial neural network" | size=600px}} | ||
| + | |||
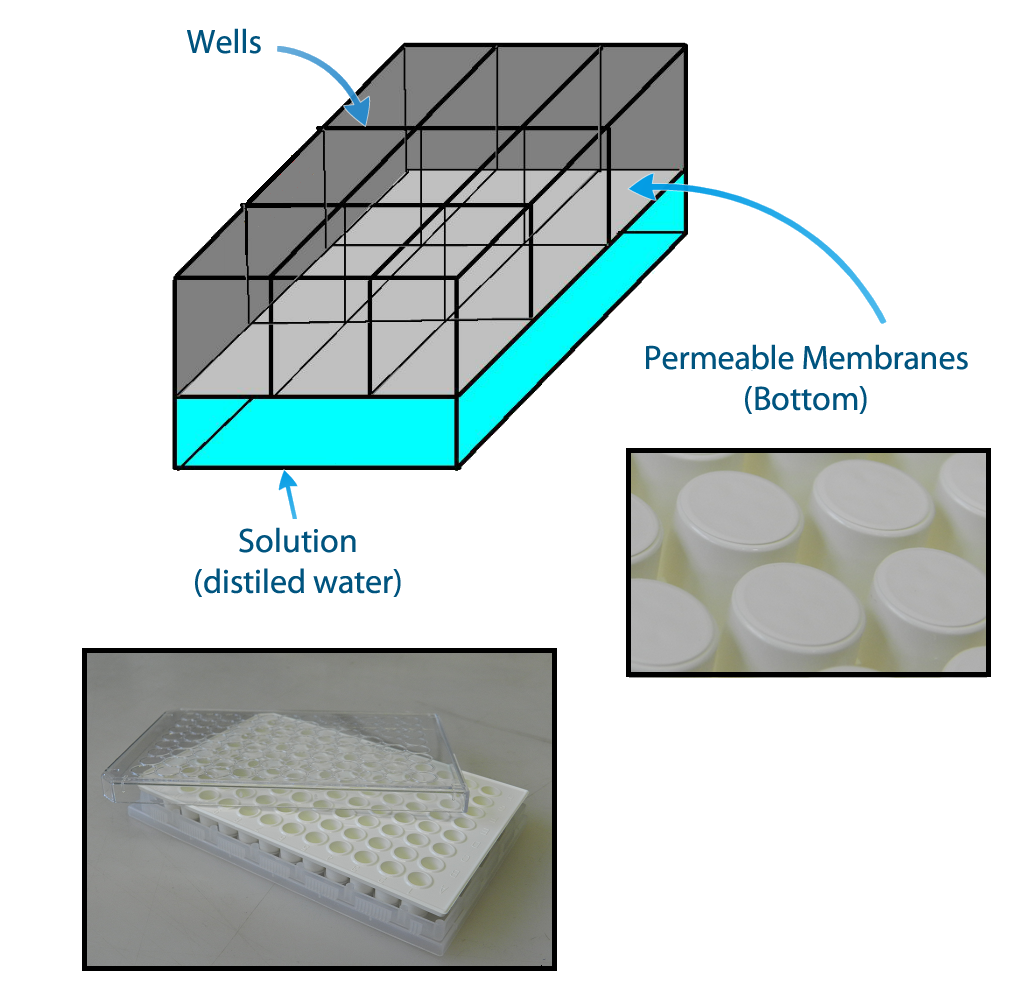
| + | In order to evaluate if one population is active, we have designed the construction of a device that keeps each population of bacteria in a fixed position and enables the communication between different populations via QSM - Figure 2. This device can be built using a plate of 96 wells with membranes attached to their bottom. The membranes allow the diffusion of the quorum sensing substances but prevent the flux of bacterial populations. | ||
| + | |||
| - | + | {{:Team:USP-UNESP-Brazil/Templates/RImage | image=Physicalsystemforbacterialnetwork.png | caption=Fig 2. Device that will be used to measure the output. | size=600px}} | |
| - | + | ====Genetic Construction==== | |
| - | + | ||
| - | + | ||
| - | + | ||
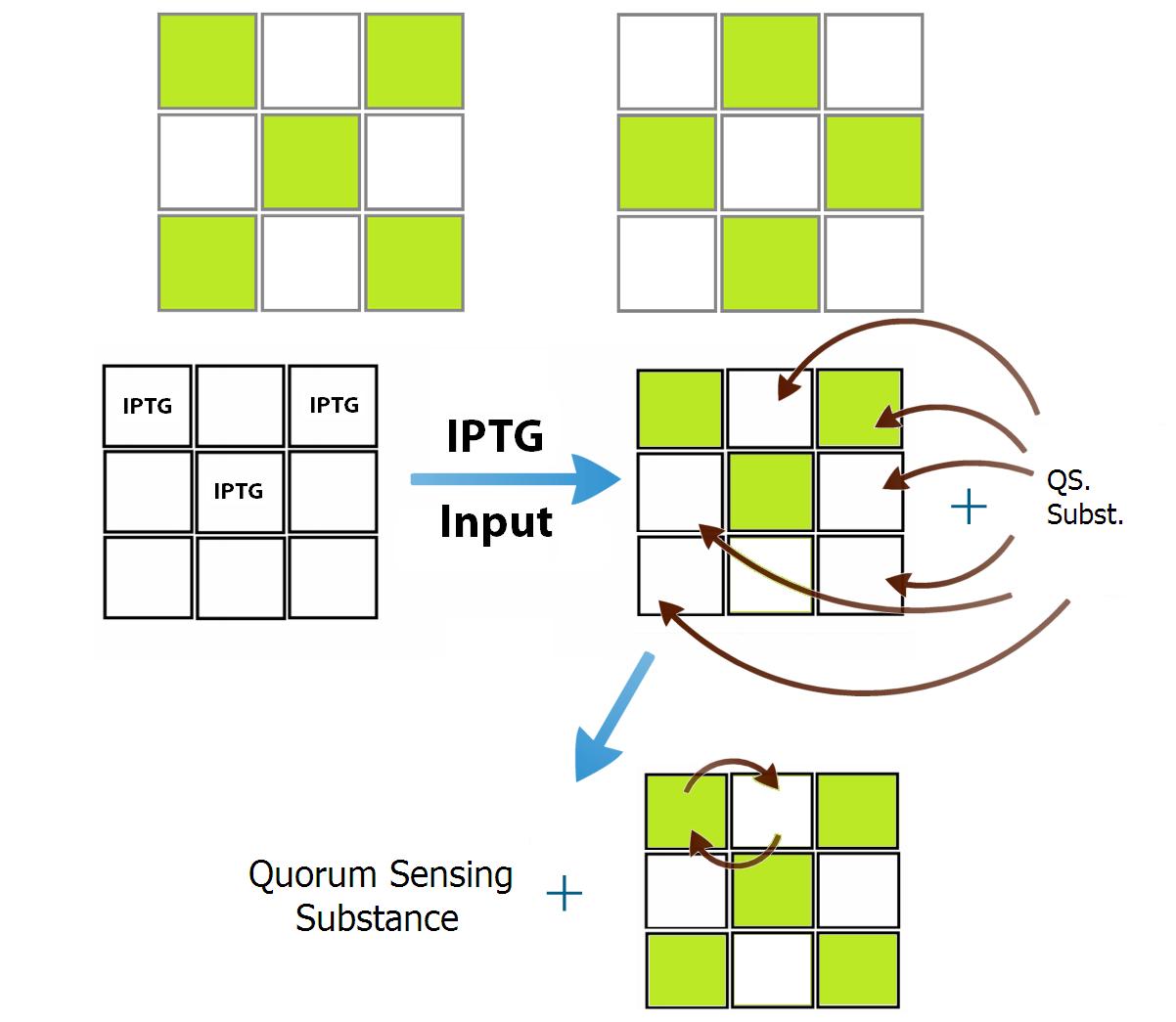
| - | + | Each population of bacteria ("neuron") is defined by the way it interacts within the network and by its own QSM. Hence, the number of "neurons" is limited to the number of QSM. As a proof of concept we designed two populations of bacteria that communicate in a repressive manner. In order to make the network visually interesting, we used our 3x3 wells device and designed the population network to recognize two patterns - Figure 3. Since they are complementary, only two different population of bacteria are needed to represent the patterns "X" and "O". In this case, each population placed at the letter "X" inhibits all the ones placed at the letter “O” and activates the positions of its own pattern (and vice-versa). | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | <!--.--> | |
| - | + | {{:Team:USP-UNESP-Brazil/Templates/RImage | image=0019.JPG | caption=Fig. 3. Representation of the input and output in the 3x3 wells device. | size=600px}} | |
| - | + | In the Registry of Parts [http://partsregistry.org/Main_Page] there are four well characterized quorum sensing systems. However, there is a strong activation crosstalk between two of them (Las and Rhl). Therefore, we decided to use the system Cin and Rhl. | |
| - | + | In our system, the QSM signals trigger the transcription of an activator (or an inhibitor) of the transcription of GFP - this is our system activation reporter. Simultaneous inhibitions and activations of a bacterial population will be converted to a molecular competition of activators and inhibitors by the promoter that controls the production of GFP. It is this molecular competition who "chooses" the pattern stored in the system that is most similar to the input. | |
| - | + | As an example, if an input activates more positions at the “X” pattern than those at the “O”, a greater number of "X-activators" will be produced, and it is more likely that other "X" positions become activated, due to this competition for promoters at each position. Meanwhile, in the “O” pattern positions, the opposite occurs: a lesser number of initially activated positions implies less "O-activators", and the outcome is that "X wins over O" - the network reproduces the "X" pattern. | |
| - | + | ||
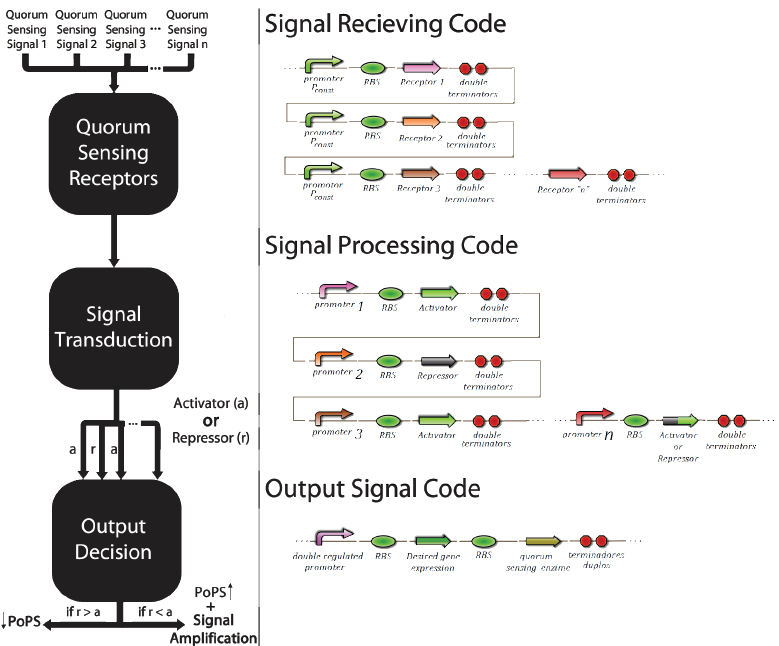
| - | The | + | This multi-regulated promoter, with an activator and an inhibitor, is called Prm. Its inhibitor is the transcriptional factor cl434 and its activator is the cl factor. The genetic design of the positions of the patterns “X” and “O” can be seen in Figure 4. |
| - | + | This construction that uses the signal transduction containing cl434 and cl allows to create different systems of associative memory, limited only by the number of quorum sensing systems available. Figure 4 shows how this generic system would work and elucidates how this system could be applied to different functions involving genetic control. | |
| - | Figure | + | |
| - | + | <!--[[File:0022.png|center|600px|caption=Fig. 4|]] --> | |
| + | {{:Team:USP-UNESP-Brazil/Templates/RImage | image=0022.png | caption=Fig. 4. Genetic construction. | size=600px}} | ||
| - | + | {{:Team:USP-UNESP-Brazil/Templates/Foot}} | |
| - | + | ||
Latest revision as of 03:47, 27 September 2012
 Introduction
Introduction Project Overview
Project Overview Plasmid Plug&Play
Plasmid Plug&Play Associative Memory
Associative MemoryNetwork
 Extras
ExtrasContents |
Background
Hopfield Associative Memory Networks
The idea of this project is based on the associative memory network introduced by J.J. Hopfield in the 80’s [http://en.wikipedia.org/wiki/Hopfield_network]. The structure of a Hopfield network is simple, all neurons are interconnected, and that brings about some interesting memory properties and provides a model for understanding human memory.
We have chosen to built a Hopfield network because of its simplicity and robustness. The same methodology can be used to the construction of networks with different architectures, such as the called “perceptrons” [http://en.wikipedia.org/wiki/Perceptron]. In contrast to a Hopfield network, a perceptron is commonly used as a classifier.
Biological Mechanism
In a biological neural network, cells occupy a specific location and the information is passed through direct physical contact - the neuron axonal projections. In our case, a population of bacteria represents a single neuron and the information is transmitted by a quorum sensing molecule (QSM). Because of that, each "neuron" has its own QSM and the number of neurons is limitated by the number of different QSM. A comparison between a biological neural network and our design is presented in Fig 1.
In order to evaluate if one population is active, we have designed the construction of a device that keeps each population of bacteria in a fixed position and enables the communication between different populations via QSM - Figure 2. This device can be built using a plate of 96 wells with membranes attached to their bottom. The membranes allow the diffusion of the quorum sensing substances but prevent the flux of bacterial populations.
Genetic Construction
Each population of bacteria ("neuron") is defined by the way it interacts within the network and by its own QSM. Hence, the number of "neurons" is limited to the number of QSM. As a proof of concept we designed two populations of bacteria that communicate in a repressive manner. In order to make the network visually interesting, we used our 3x3 wells device and designed the population network to recognize two patterns - Figure 3. Since they are complementary, only two different population of bacteria are needed to represent the patterns "X" and "O". In this case, each population placed at the letter "X" inhibits all the ones placed at the letter “O” and activates the positions of its own pattern (and vice-versa).
In the Registry of Parts [http://partsregistry.org/Main_Page] there are four well characterized quorum sensing systems. However, there is a strong activation crosstalk between two of them (Las and Rhl). Therefore, we decided to use the system Cin and Rhl.
In our system, the QSM signals trigger the transcription of an activator (or an inhibitor) of the transcription of GFP - this is our system activation reporter. Simultaneous inhibitions and activations of a bacterial population will be converted to a molecular competition of activators and inhibitors by the promoter that controls the production of GFP. It is this molecular competition who "chooses" the pattern stored in the system that is most similar to the input.
As an example, if an input activates more positions at the “X” pattern than those at the “O”, a greater number of "X-activators" will be produced, and it is more likely that other "X" positions become activated, due to this competition for promoters at each position. Meanwhile, in the “O” pattern positions, the opposite occurs: a lesser number of initially activated positions implies less "O-activators", and the outcome is that "X wins over O" - the network reproduces the "X" pattern.
This multi-regulated promoter, with an activator and an inhibitor, is called Prm. Its inhibitor is the transcriptional factor cl434 and its activator is the cl factor. The genetic design of the positions of the patterns “X” and “O” can be seen in Figure 4.
This construction that uses the signal transduction containing cl434 and cl allows to create different systems of associative memory, limited only by the number of quorum sensing systems available. Figure 4 shows how this generic system would work and elucidates how this system could be applied to different functions involving genetic control.
 "
"